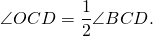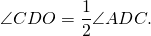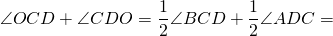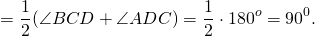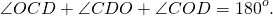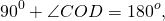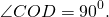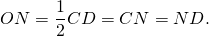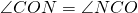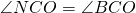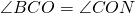Как доказать что биссектрисы пересекаются в одной точке в трапеции
Как доказать что биссектрисы пересекаются в одной точке в трапеции
Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.
a) Расстояние от центра окружности до хорд одинаковой длины равны. Следовательно, точка O равноудалена от прямых AB, BC, CD и AD. Значит, она лежит на биссектрисе каждого из углов трапеции.
б) Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда UW — высота трапеции, а точка V — середина отрезка KL. Значит,
Пусть BH — высота трапеции. В прямоугольном треугольнике ABH имеем:
Приведем решение Максима Волкова.
Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда
UW — высота трапеции, а точка V — середина отрезка KL. Тогда
Проведем отрезки АО и ОВ. Заметим, что треугольник AOB прямоугольный, так как АО и ВО — биссектрисы углов трапеции при боковой стороне. Тогда по свойству высоты прямоугольного треугольника находим:
Следовательно, для высоты трапеции получаем:
Аналоги к заданию № 520805: 520917 520855 520881 Все
Как доказать что биссектрисы пересекаются в одной точке в трапеции
Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.
a) Расстояние от центра окружности до хорд одинаковой длины равны. Следовательно, точка O равноудалена от прямых AB, BC, CD и AD. Значит, она лежит на биссектрисе каждого из углов трапеции.
б) Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда UW — высота трапеции, а точка V — середина отрезка KL. Значит,
Пусть BH — высота трапеции. В прямоугольном треугольнике ABH имеем:
Приведем решение Максима Волкова.
Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда
UW — высота трапеции, а точка V — середина отрезка KL. Тогда
Проведем отрезки АО и ОВ. Заметим, что треугольник AOB прямоугольный, так как АО и ВО — биссектрисы углов трапеции при боковой стороне. Тогда по свойству высоты прямоугольного треугольника находим:
Следовательно, для высоты трапеции получаем:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 520805: 520917 520855 520881 Все
Биссектрисы углов при боковой стороне трапеции
Рассмотрим два полезных свойства, которыми обладают биссектрисы углов при боковой стороне трапеции.
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

CO — биссектриса ∠BCD,
DO — биссектриса ∠ADC.
∠ADC+∠BCD=180º (как внутренние односторонние углы при AD ∥ BC и секущей CD).
Так как CO — биссектриса ∠BCD, то
Так как DO — биссектриса ∠ADC,
По теореме о сумме углов треугольника

Что и требовалось доказать.
Биссектрисы углов при боковых сторонах трапеции пересекаются в точке, лежащей на средней линии трапеции.
Дано: ABCD — трапеция, AD ∥ BC,
CO — биссектриса ∠BCD,
DO — биссектриса ∠ADC,
MN — средняя линия трапеции.

Проведем из вершины прямого угла COD медиану ON.
2) Так как ON=CN, треугольник OCN — равнобедренный с основанием OC.
(как углы при основании равнобедренного треугольника).
Так как CO — биссектриса ∠BCD,
А так как эти углы — внутренние накрест лежащие при ON и BC и секущей OC, то ON ∥ BC (по признаку параллельности прямых).

Узнать ещё
Знание — сила. Познавательная информация
Биссектрисы трапеции
Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.
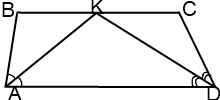
I. Биссектрисы углов при боковой стороне трапеции пересекаются.
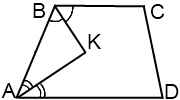
2) ∠ ABK+ ∠ KAB=( ∠ ABC+ ∠ BAD):2=90 º (так как биссектрисы делят углы пополам).
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.
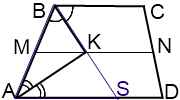
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN ∥ AD.
Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK ∥ AS.
Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
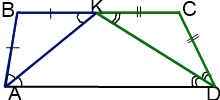
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.
В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
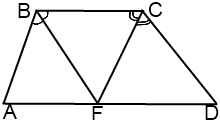
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Как доказать что биссектрисы пересекаются в одной точке в трапеции
Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 15, KL = 6, LB = 5.
a) Расстояние от центра окружности до хорд одинаковой длины равны. Следовательно, точка O равноудалена от прямых AB, BC, CD и AD. Значит, она лежит на биссектрисе каждого из углов трапеции.
б) Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда UW — высота трапеции, а точка V — середина отрезка KL. Значит,
Пусть BH — высота трапеции. В прямоугольном треугольнике ABH имеем:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 520805: 520917 520855 520881 Все