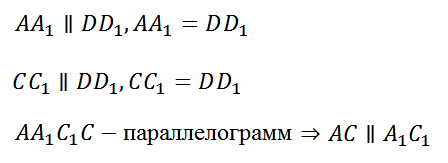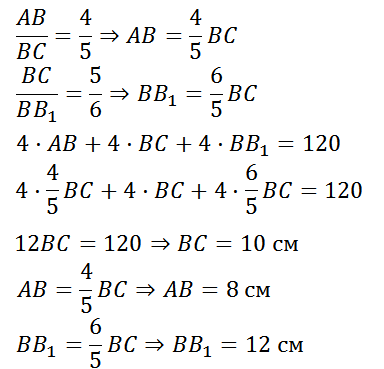Как доказать что фигура является параллелепипедом
Параллелепипед (ЕГЭ 2022)
Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Читай статью, смотри вебинар и ты все про него будешь знать!
Параллелепипед — коротко о главном
Параллелепипед — это четырехугольная призма (многогранник с \( \displaystyle 6\) гранями), все грани которой — параллелограммы.
Прямой параллелепипед —это параллелепипед, у которого \( \displaystyle 4\) боковые грани — прямоугольники.
Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники
Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства параллелепипеда
Параллелепипед — подробнее
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
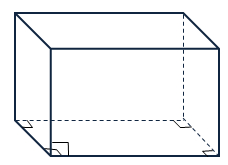
Если слишком сложно, просто посмотри на картинку.
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.
Далее смотри на картинки, запоминай и не путай!
Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
Свойства параллелепипеда
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.
Прямой параллелепипед
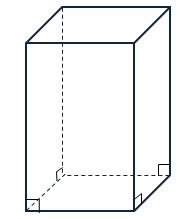
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольный параллелепипед
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:
У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.
Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.\( \displaystyle <
^<2>>=<^<2>>+<^<2>>+< ^<2>>\).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Прямоугольный параллелепипед. Что это такое?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
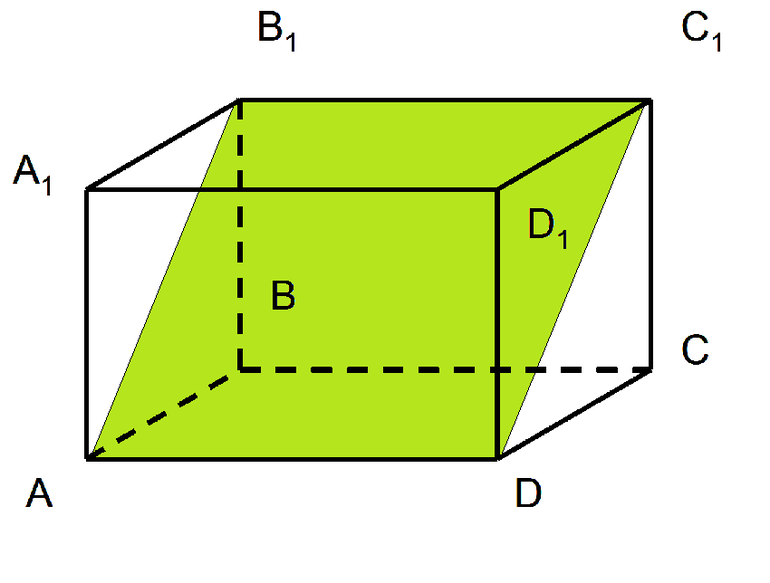
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
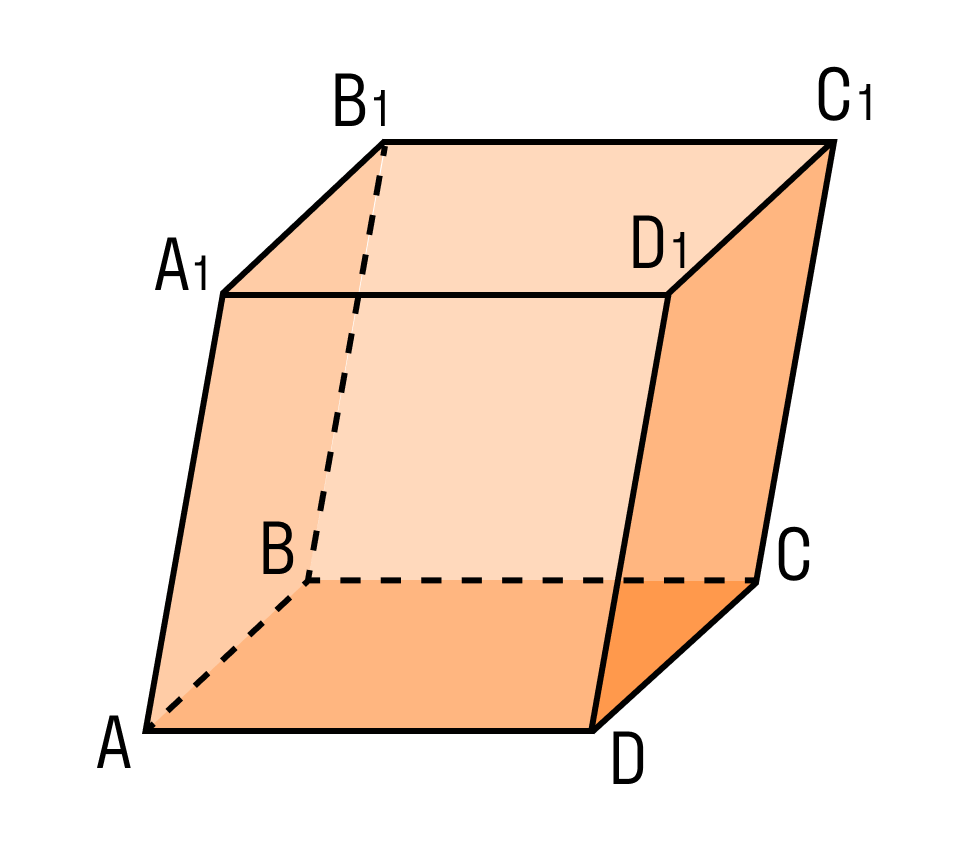
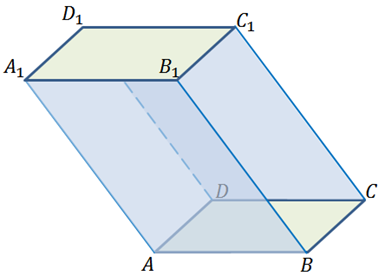
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
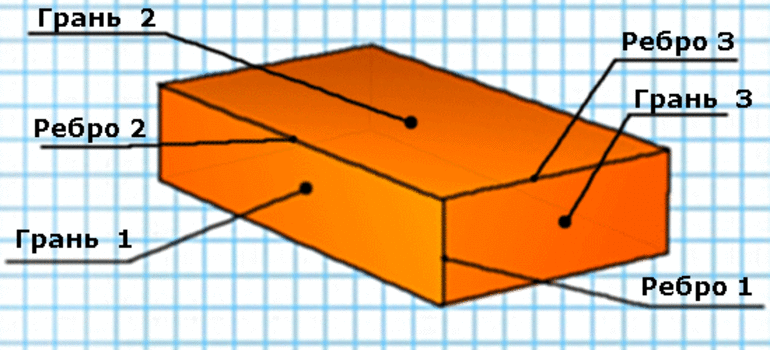
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
Формулы прямоугольного параллелепипеда:
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
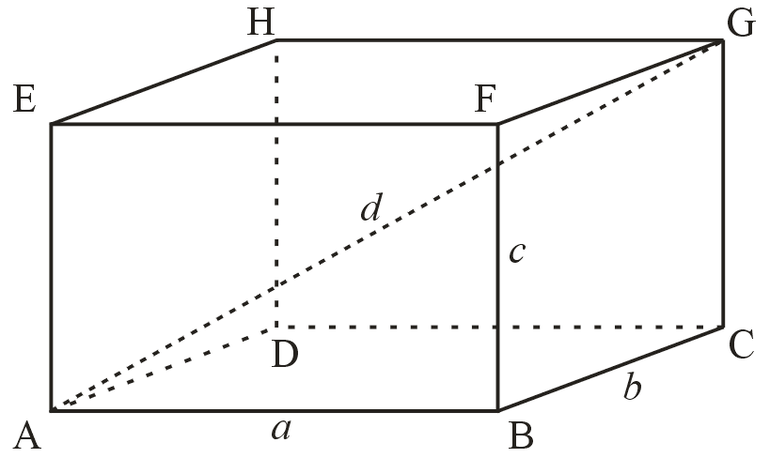
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
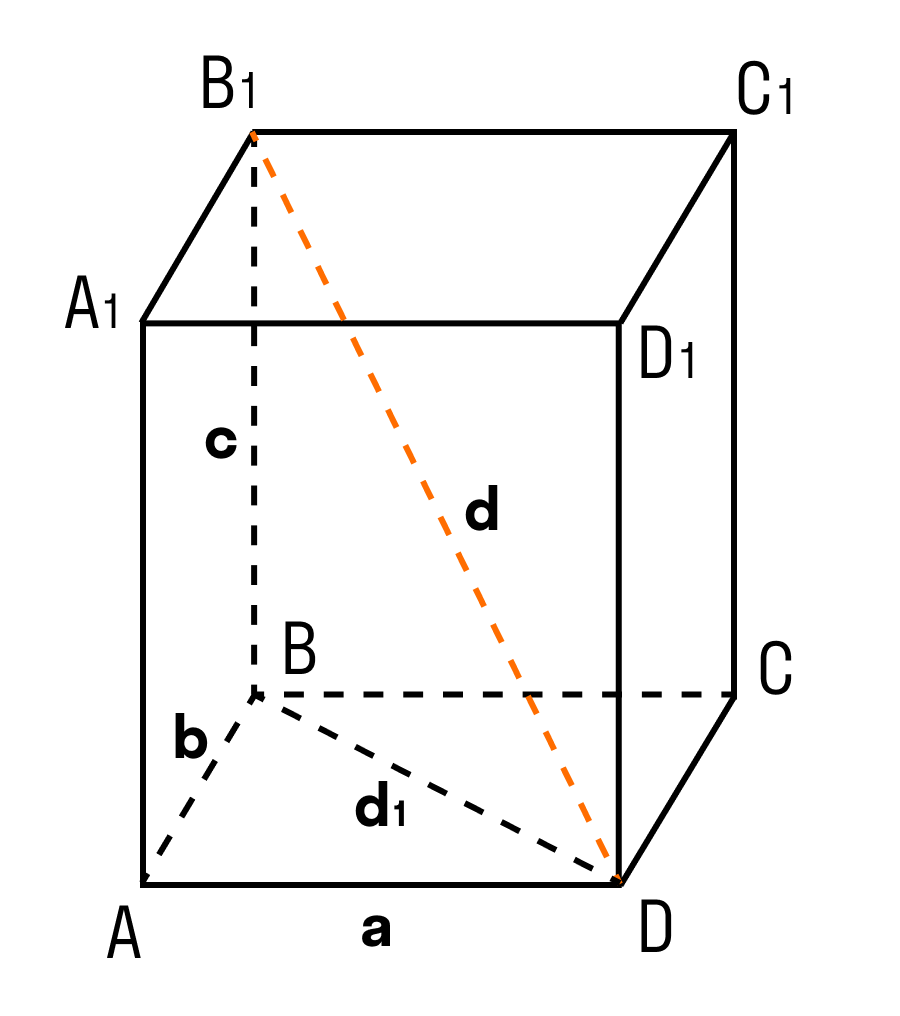
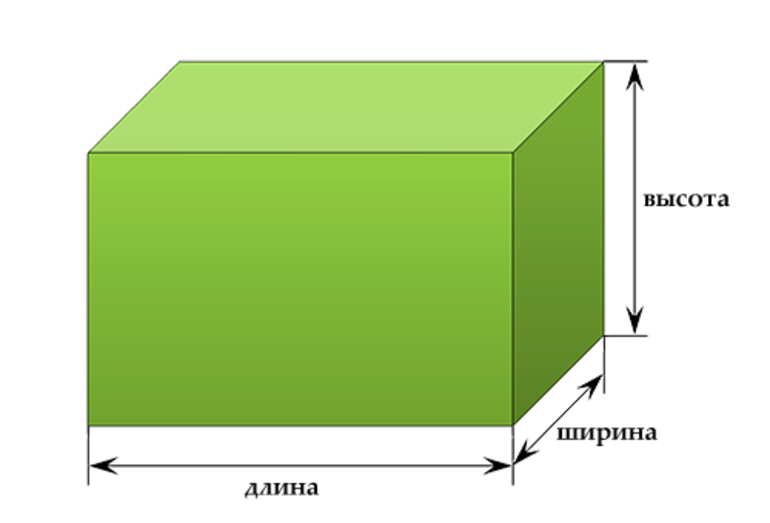
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
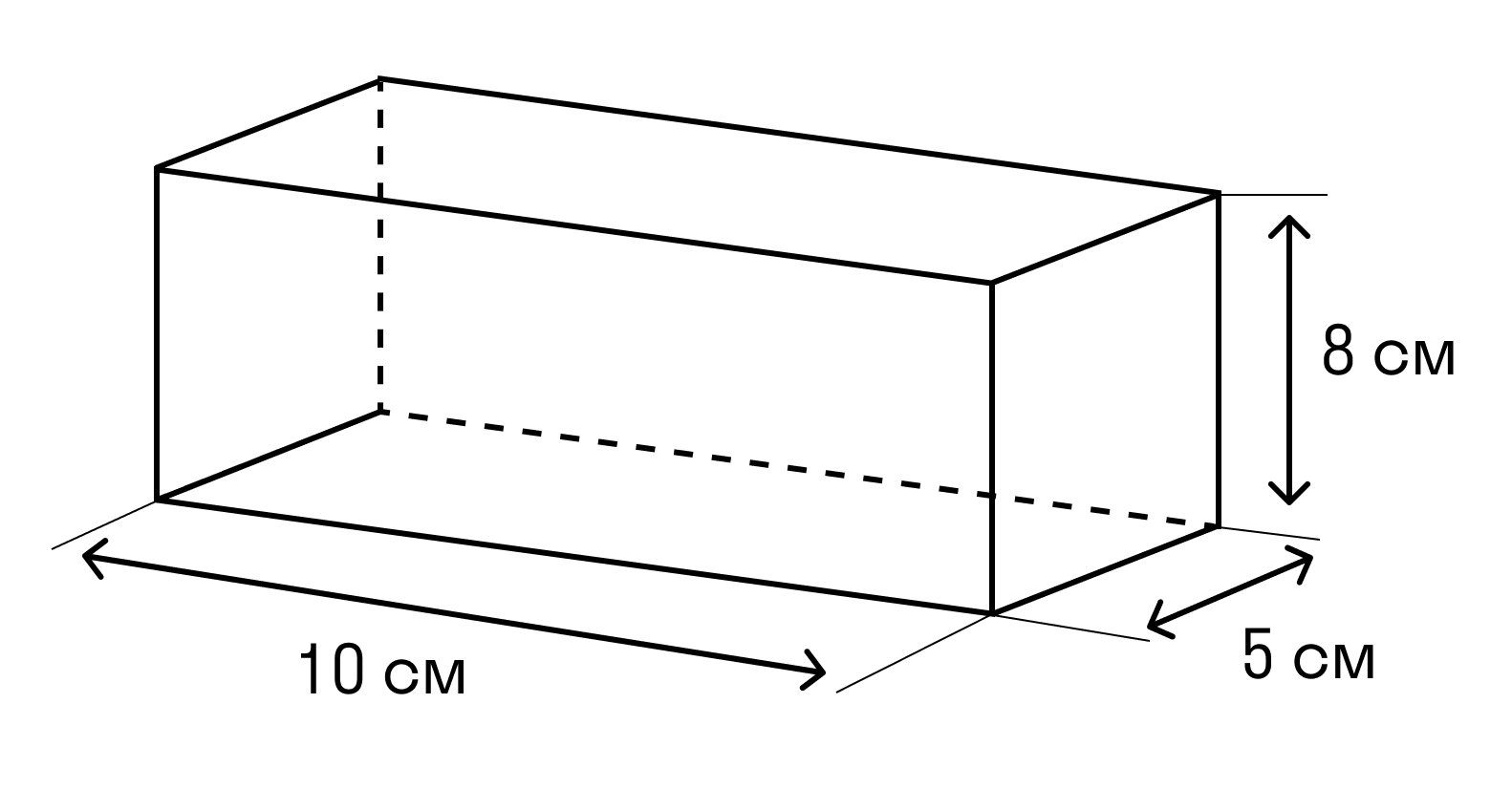
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
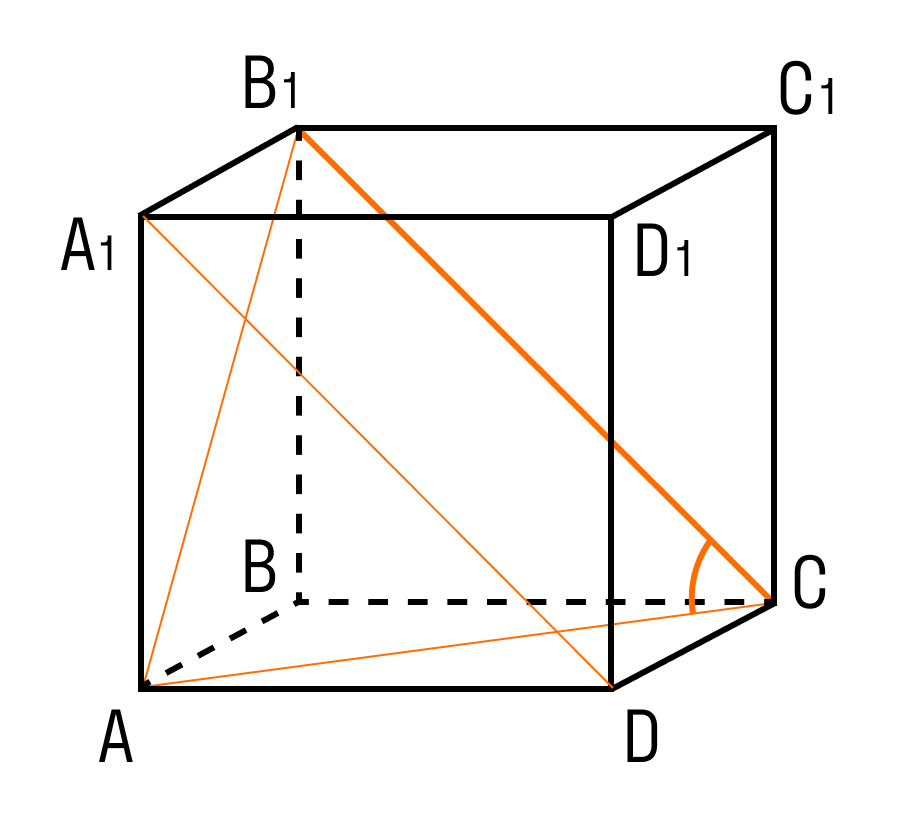
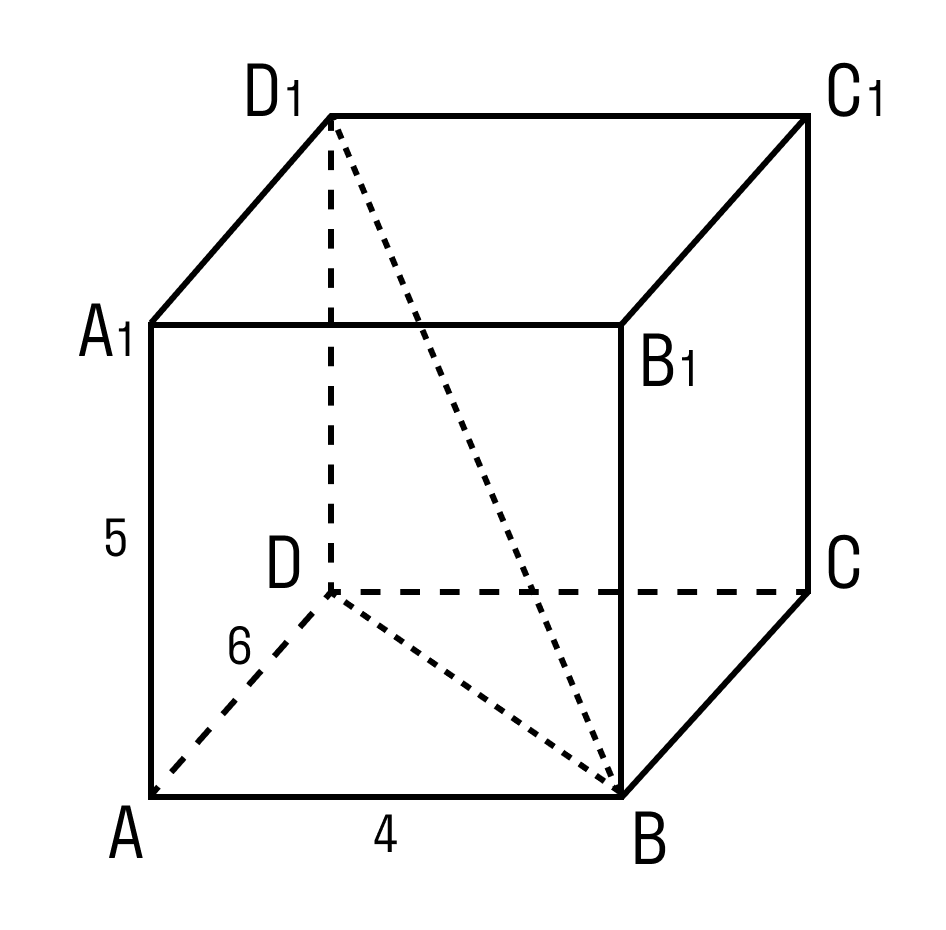
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.
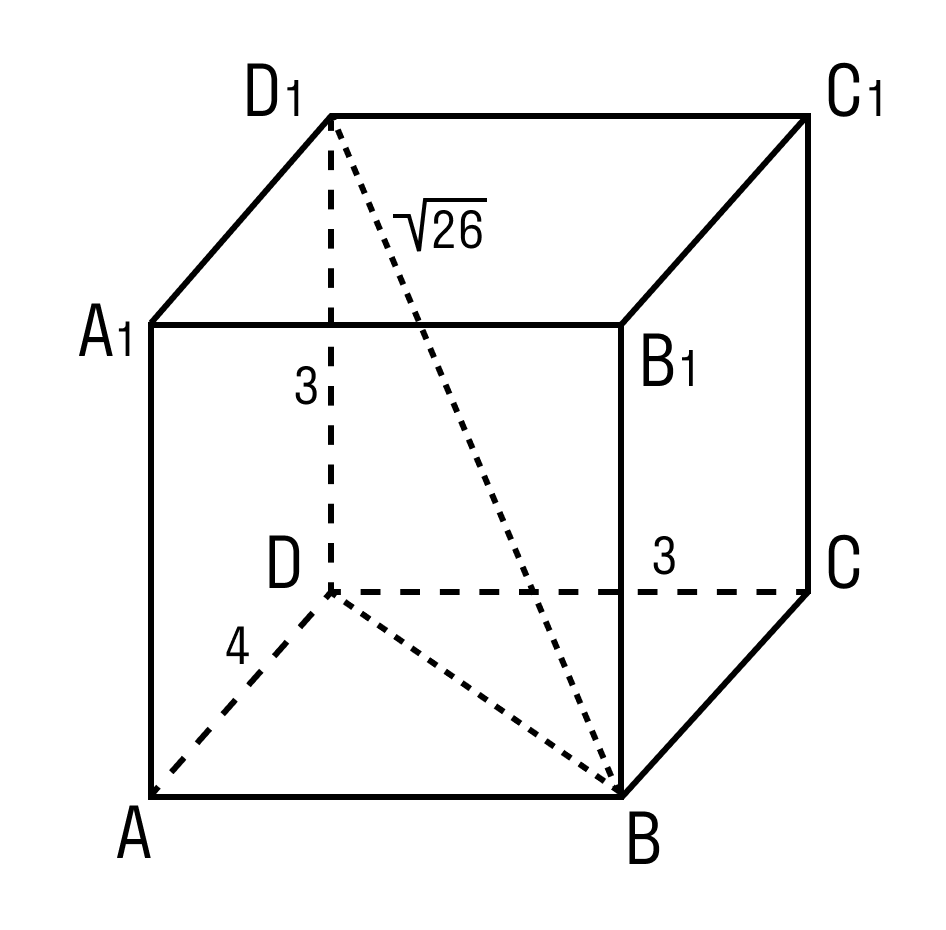
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
Общая характеристика
В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.
Основные понятия и классификация
Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.
Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:
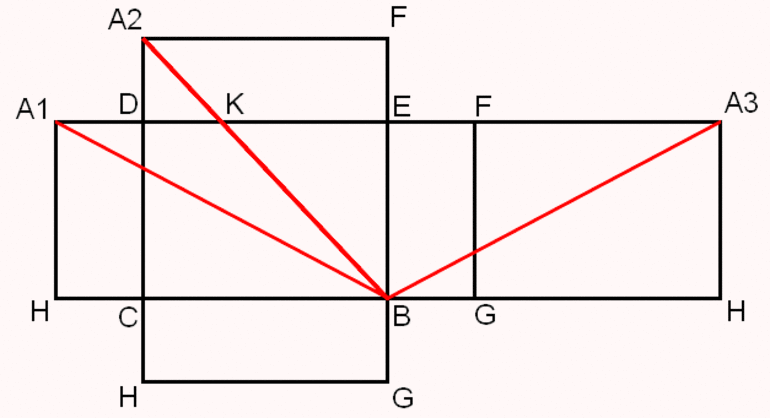
В 6 классе на уроке геометрии изучают планиметрию (плоские фигуры). Здесь представлена развертка плоскостей.
Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.
При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием. Свойства параллелепипеда:
Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.
Диагонали поверхности пересекаются и этой центральной точкой делятся на несколько частей. Они равны d2=a2+b2+c2
Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.
Формулы и анализ
Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:
Расшифровка обозначений: V — объем фигуры, S — площадь поверхности, a — длина, b — ширина, c — высота.
Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.
Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.
Для нахождения ответов недостаточно знать только свойства геометрической фигуры. Могут пригодиться формулы для вычисления S и V.
Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.
∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.
∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.
Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.
S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:
Объем фигуры равен величине смешанного произведения нескольких векторов, выпущенных из единой точки.
Практическое применение
Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.
Доказательство теорем
Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).
Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.
Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.
Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.
Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.
Решение задач
Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.
Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.
Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.
Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).
Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.
Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.
Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:
Ответ: объем составляет 576.
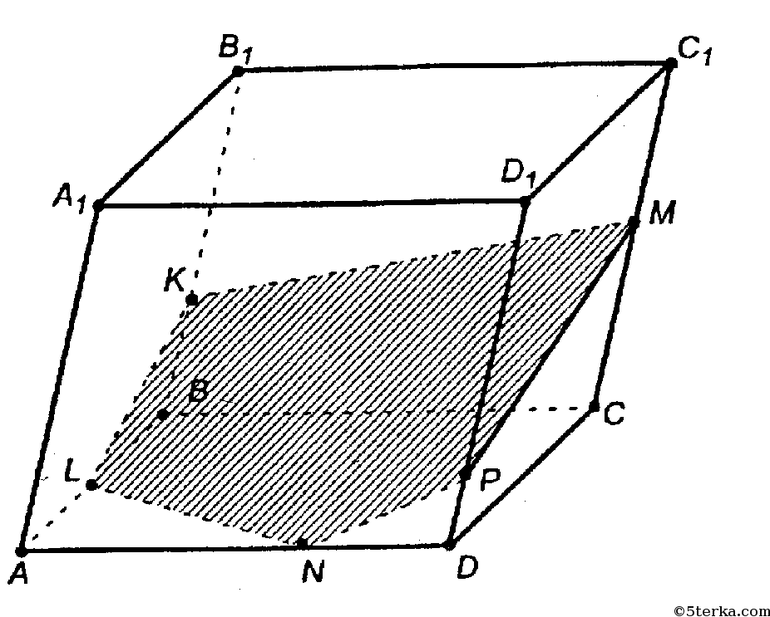
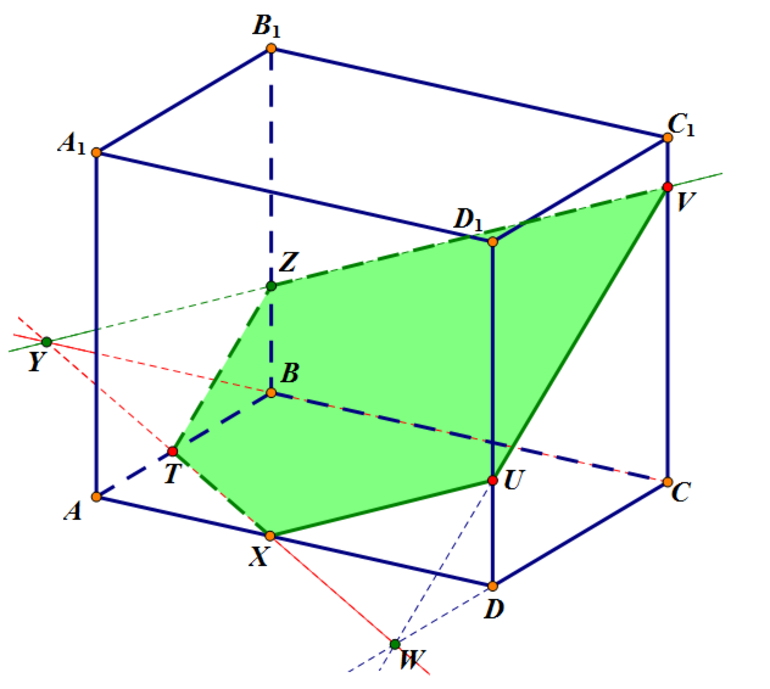
Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.
KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².
Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.
В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.
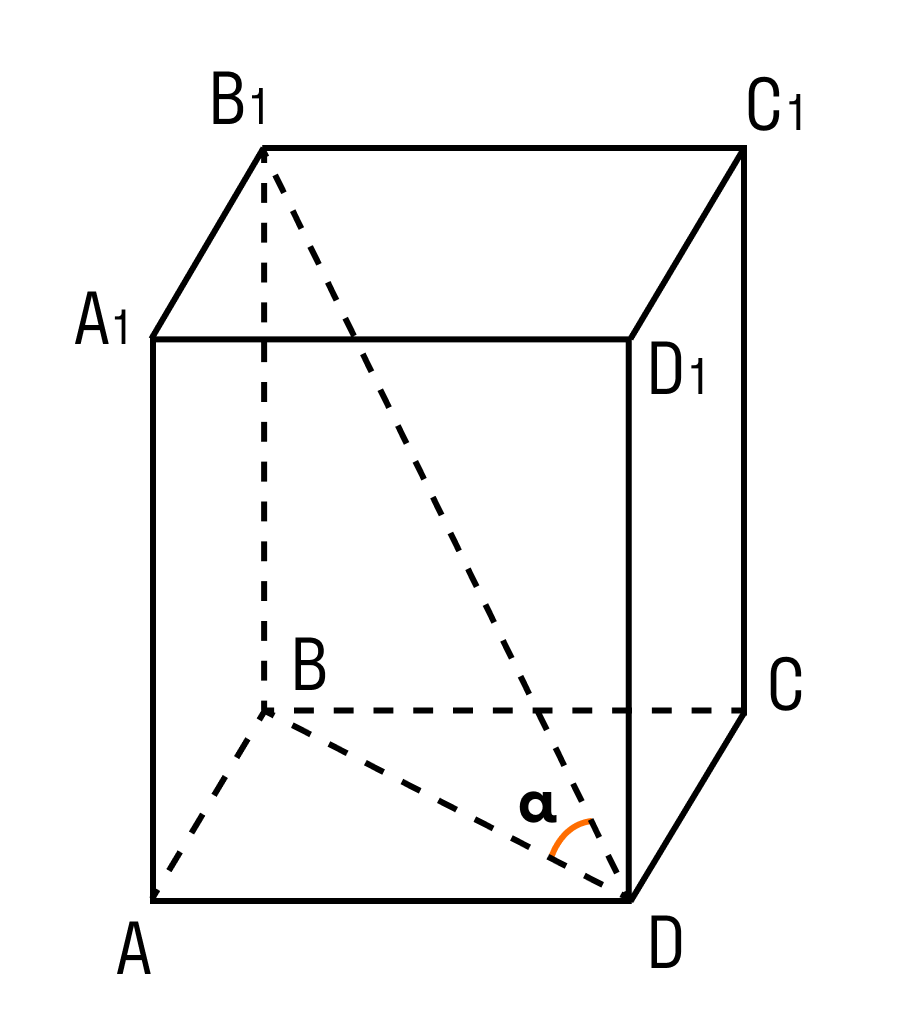
Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.
Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.
В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.
Высота треугольника делит его основание пополам. По теореме Пифагора она равна:
Высота фигуры составляет 3 см.
Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.
Параллелипипед
Урок 13. Геометрия 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Параллелипипед»
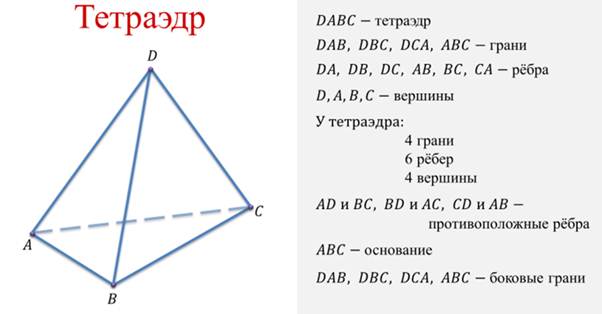
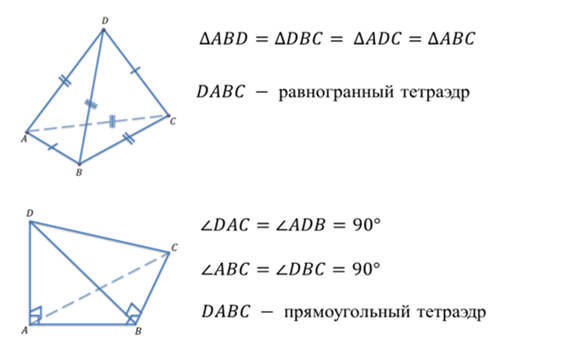
Прежде чем приступить к изучению нового материала, давайте вспомним, какая фигура называется тетраэдром, вспомним элементы тетраэдра и виды тетраэдра.
С параллелепипедом мы уже знакомы. Напомним, что в курсе геометрии базовой школы мы определяли параллелепипед как четырехугольную призму, основаниями которой являются параллелограммы.
Сегодня мы дадим немного другое определение параллелограмма.
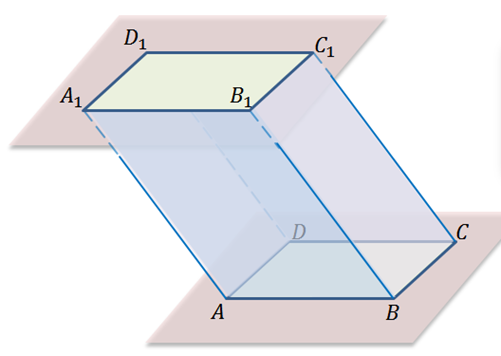
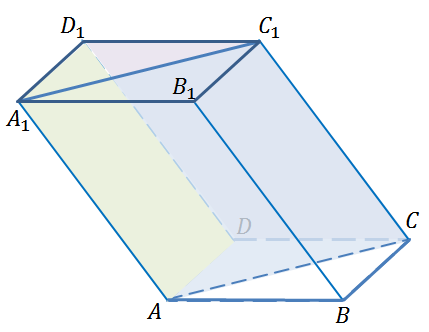
Рассмотрим два равных параллелограмма ABCD и A1B1C1D1, которые расположены в параллельных плоскостях так, что отрезки AA1, BB1, CC1, DD1 параллельны.
Получили четырехугольники ABB1A1, BCC1B1, CDD1C1, DAA1D1. Рассмотрим один из этих четырехугольников. Например, четырехугольник ABB1A1. Стороны AA1 и BB1 параллельны по условию. По свойству параллельных плоскостей стороны AB и A1B1 параллельны. То есть, четырехугольник ABB1A1 – параллелограмм, аналогично, параллелограммами будут каждый из четырехугольников BCC1B1, CDD1C1, DAA1D1.
Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов ABB1A1, BCC1B1, CDD1C1, DAA1D1называется параллелепипедом и обозначается так: ABCDA1B1C1D1
Параллелограммы, из которых составлен параллелепипед, называются гранями.
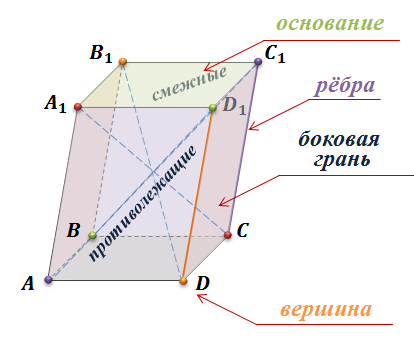
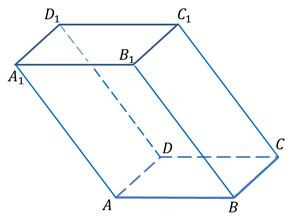
На рисунке изображен параллелепипед ABCDA1B1C1D1. Обратите внимание, все шесть граней параллелепипеда – параллелограммы.
Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра. Например, грани AA1B1B и DD1C1C – противолежащие.
Грани имеющие общее ребро называются смежными. Например, грани AA1D1D и DD1C1C – смежные, ребро DD1 у них общее.
Две вершины, которые не принадлежат одной грани, называются противоположными.
Отрезок, который соединяет противоположные вершины, называется диагональю параллелепипеда. Соответственно у параллелепипеда есть четыре диагонали.
То есть, если в качестве оснований выбрать грани ABCDиA1B1C1D1, то боковыми гранями будут параллелограммы ABB1A1, BCC1B1, CDD1C1, DAA1D1, а боковыми рёбрами будут отрезки AA1, BB1, CC1, DD1.
Мы уже знаем, как изображается параллелепипед. Как и в прочих пространственных фигурах, невидимые рёбра и другие отрезки изображаются штриховыми линиями.
Со свойствами параллелепипеда мы уже знакомы. Повторим их еще раз и докажем с учетом нового определения параллелепипеда.
Первое свойство звучит так: противоположные грани параллелепипеда параллельны и равны. Сразу отметим, что две грани параллелепипеда будут параллельны, если их плоскости параллельны.
Докажем, например, параллельность и равенство граней ABB1A1 и DCC1D1 параллелепипеда ABCDA1B1C1D1. Поскольку эти грани являются параллелограммами, то можно записать, что AB параллельно DC и AA1 параллельно DD1. То есть две пересекающиеся прямые AB и AA1 одной грани соответственно параллельны двум пересекающимся прямым CD и DD1 другой грани. Значит, по признаку параллельности плоскостей получим, что грани ABB1A1 и DCC1D1 параллельны.
Поскольку все грани параллелепипеда – параллелограммы, то можно записать, что AB равно DC и AA1равно DD1. По этой же причине стороны углов A1AB и D1DC соответственно сонаправлены, и, значит, эти углы равны. Таком, образом мы доказали, что две смежные стороны и угол между ними параллелограмма ABB1A1 соответственно равны двум смежным сторонам и углу между ними параллелограмма DCC1D1, поэтому параллелограммы ABB1A1 и DCC1D1 равны.
Перейдем ко второму свойству. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Доказательство этого утверждения основывается на следующем факте: если две прямые в пространстве параллельны третьей прямой, то они параллельны.
Мы знаем, что диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
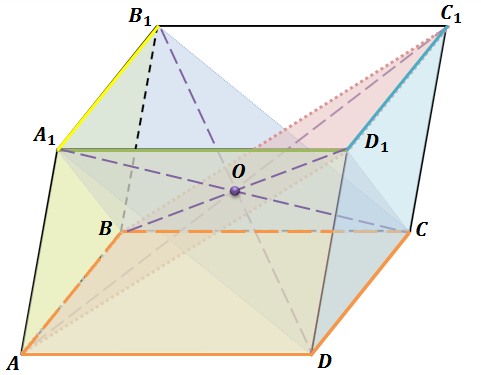
Итак, на экране изображен прямоугольный параллелепипед ABCDA1B1C1D1. Поскольку грани ABCDи AA1D1D – параллелограммы, то BC параллельно AD, BC равно AD, A1D1 параллельно AD, A1D1 равно AD. Из этого следует, что A1D1 параллельно BC и A1D1 равно BC. Поэтому четырехугольник A1D1CB – параллелограмм. А значит, его диагонали A1C и D1B пересекаются в некоторой точке О и делятся этой точкой пополам. Заметим, что эти же диагонали A1C и D1B являются также диагоналями параллелепипеда.
Поскольку грани ABCDиDD1C1C– параллелограммы, то AB параллельно CD, AB равно CD, C1D1 параллельно CD, C1D1 равно CD. Из этого следует, что C1D1 параллельно AB и C1D1 равно AB. Поэтому четырехугольник C1D1AB – параллелограмм. И, следовательно, его диагонали C1A и D1B пересекаются и точкой пересечения делятся пополам. Но серединой диагонали D1B является точка О. Таким образом, диагонали A1C, D1B и C1A параллелепипеда пересекаются в точке О и делятся этой точкой пополам.
Поскольку грани ABCDи AA1B1B – параллелограммы, то CD параллельно AB, CD равно AB, A1B1 параллельно AB, A1B1 равно AB. Из этого следует, что A1B1 равно CD и A1B1 параллельно CD. Поэтому четырехугольник A1B1CD – параллелограмм. И, следовательно, его диагонали A1C и B1D пересекаются и точкой пересечения делятся пополам. Но серединой диагонали A1C является точка О. Таким образом, все четыре диагонали A1C, B1D, C1A и D1B параллелепипеда пересекаются в точке О и делятся этой точкой пополам. Что и требовалось доказать.
Слово параллелепипед происходит от древнегреческих слов паралелос – параллельный, и епипед – плоскость.
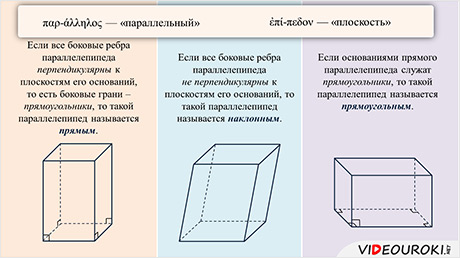
Если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым.
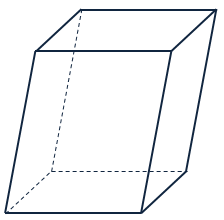
Если параллелепипед не является прямым, то есть если все его боковые ребра не перпендикулярны к плоскостям оснований, то он называется наклонным.
Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
Параллелепипед очень часто встречается в жизни, практически все здания имеют форму параллелепипеда. И многие предметы имеют форму параллелепипеда.
Решим несколько задач.
Задача. Дан параллелепипед 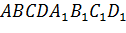
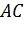
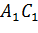
Что и требовалось доказать.
Задача. Сумма всех рёбер параллелепипеда 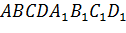
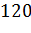
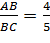
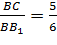
Из соотношений выразим длины ребер AB и BB1 через длину ребра BC.
Получим, что ABравно 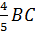
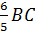
У параллелепипеда двенадцать ребер, из них четыре ребра равны ребру AB, четыре ребра равны ребру BB1, четыре ребра равны ребру BC. Заменим ребра AB и BB1 и их выражением через ребро BC, получим, что 12BC=120. Тогда получим, что длина ребра BC= 10. Подставим это значение в формулу для нахождения длин ребер AB и BB1, получим, что AB= 8, а BB1= 12.
Кратко запишем решение задачи.
Подведем итоги урока. Сегодня на уроке мы познакомились с еще одним пространственнымтелом – параллелепипедом. Познакомились с элементами параллелепипеда, решили несколько задач по данной теме.