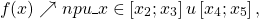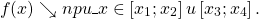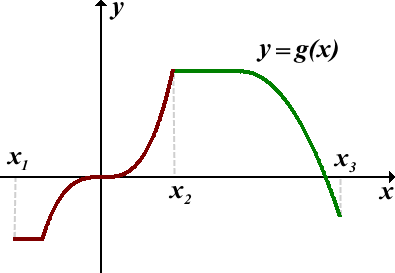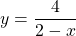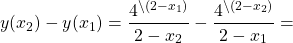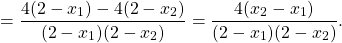Как доказать что функция убывает на промежутке 9 класс

Тема урока: «Возрастание и убывание функций»

Разделы: Математика

В настоящее время существует противоречие между потребностью старшеклассников к проявлению творчества, активности, самостоятельности, самореализации и ограниченностью времени для этого на уроках математики. Начиная с 2006 года я использую учебники «Алгебра 7, 8, 9» с углубленным изучением математики Ю. Н. Макарычева, Н. Г. Миндюка, К. И. Нешкова для учащихся математических классов с целью совершения осознанного выбора учащимися профиля обучения, предоставления ученикам возможности работы на уровне повышенных математических требований, развития их учебной мотивации.
Как включить учеников в самостоятельную исследовательскую деятельность, чтобы они сами «открывали» новые свойства и отношения, а не получали их от учителя в готовом виде? Многолетний опыт работы и желание изменить в себе традиционные представления об обучении подтолкнули меня к применению исследовательской деятельности на своих уроках математики. Конечно, изменение метода работы, структуры урока и принятия на себя функции организатора процесса познания, функции обеспечивающего системное включение каждого ученика, независимо от интеллектуального уровня, в основные виды деятельности, потребовало от меня определенных знаний и готовности к саморазвитию.
Я думаю, что включение учащегося в деятельность влияет и на глубину и прочность усвоения ими знаний, и на формирование у него системы ценностей, то есть самовоспитание. Наличие у учеников способностей к саморазвитию и самовоспитанию позволит им успешно адаптироваться к постоянно изменяющимся внешним условиям, не вступая при этом в конфликт с обществом.

Тема раздела: «Свойства функций».

Тема урока: «Возрастание и убывание функций».

Тип урока: урок изучения и первичного применения нового материала.

I. Актуализация опорных знаний

– Дайте определение функции.
– Какой формулой задаются функции, графики которых изображены на чертеже. (Приложение 2)

II. Формирование новых знаний

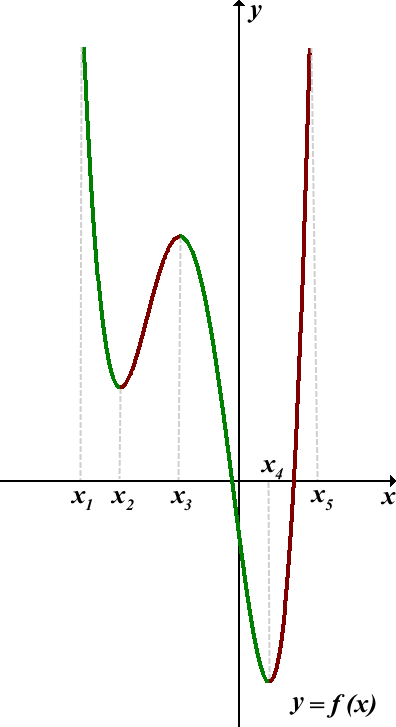
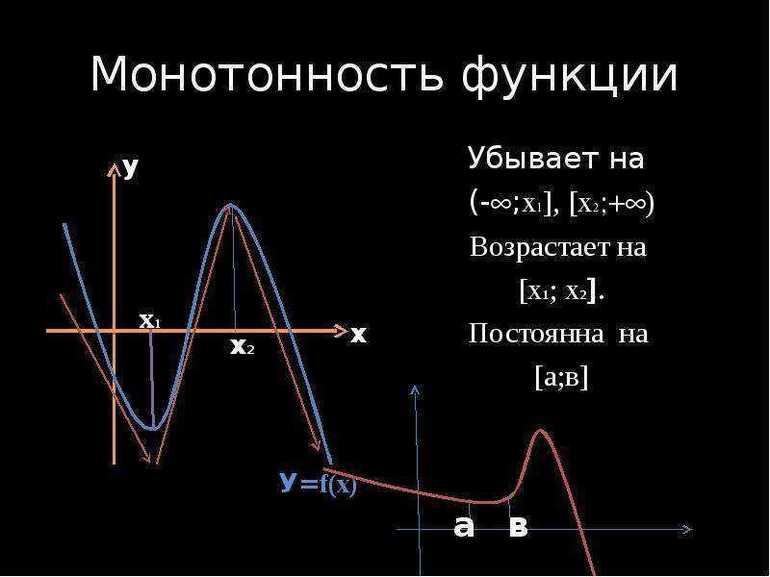
На рисунке 1 (Рисунок 1, Приложение 1) изображен график некоторой функции у = f (х), область определения которой – промежуток [–5; 4].
При возрастании значений X от –5 до 1 значения Y возрастают, а при возрастании значений X от 1 до 4 значения Y убывают. Говорят, что функция у = f (х) на промежутке [–5; 1] возрастает, а на промежутке [1; 4] – убывает.

f(х₂) – f(х₁) = – = ( – ) ( +) / ( +) = .

Числитель и знаменатель дроби – положительные числа. Это следует из того, что х₂ > х₁ > 0, > 0 и > 0. Значит, f(х₂) – f(х₁) > 0, то есть f(х₂) > f(х₁). Поэтому функция f(х) возрастающая. (Приложение 5)

Работая в парах учащиеся проговаривают друг другу какие свойства монотонных функций использовали. (Приложение 13)
Решите уравнение: х 5 + х 3 + х = – 42.
Решите систему уравнений:

+ (х – у) 3 = 2, х 2 – 6у + 1 = 0.

V. Итог урока

VI. Домашнее задание (Приложение 15)

1. Докажите, что функция g(х) является убывающей функцией:

а) g(х) = , где х > – .
б) g (х) = .

2. Докажите, что функция f(х) является возрастающей функцией:

3. Решите уравнение: х 2 + – = 15.

Источник

Возрастание и убывание функций

1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

x_1 \Rightarrow f(x_2 ) > f(x_1 ). \]» title=»Rendered by QuickLaTeX.com»/>

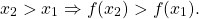
2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

x_1 \Rightarrow f(x_2 )

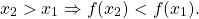
Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.

График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).

На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).

Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x₁;x₅]:

Кратко это записывают так:

3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).

4) Если функция возрастает на всей своей области определения, то её называют возрастающей.

Если функция убывает на всей своей области определения, то её называют убывающей.

Например, y=√x, y=x³ — возрастающие функции.

Линейная функция y=kx+b возрастающая при k>0 и убывающая при k 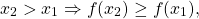x_1 \Rightarrow f(x_2 ) \ge f(x_1 ), \]» title=»Rendered by QuickLaTeX.com»/>

то функция y=f(x) называется неубывающей на этом промежутке.

6) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

x_1 \Rightarrow f(x_2 ) \le f(x_1 ), \]» title=»Rendered by QuickLaTeX.com»/>

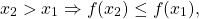
то функция y=f(x) называется невозрастающей на этом промежутке.

7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.

Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x₁;x₃], является невозрастающей и неубывающей:

Функция y=g(x) является неубывающей на промежутке [x₁;x₂].

Функция y=g(x) является невозрастающей на промежутке [x₂;x₃].

Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.

Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?

группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:

Теперь выносим общий множитель (x₂-x₁) за скобки:

Так как x₂>x₁, то x₂-x₁>0. Следовательно, знак произведения зависит от знака второго множителя.

Для x₁, x₂ ∈(-∞;-2) x₂+x₁+4

возрастает на промежутке (2;+∞).

Функция определена при x∈(-∞;2) и (2;+∞).

0. \]» title=»Rendered by QuickLaTeX.com»/>

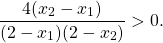
Отсюда y(x₂)-y(x₁)>0. Поэтому данная функция возрастает на промежутке (2;+∞).

Что и требовалось доказать.

Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).

Источник

Общие сведения

Функцией вида р = f(r) называется зависимость ее значения от переменной величины «r» или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.

Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) = f(r2) соответственно. Кроме того, нужно учитывать, что r1 =» следует заменить на строгий « »: f(r1) f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:

Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.

Теорема о пределе

Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.

Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.

Критерии возрастания и убывания

Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:

Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) = 0 соответственно (при r ∈ данному интервалу).

Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) 0.

Основные свойства

Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:

После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.

Базовые знания

Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:

Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.

Нахождение производной

Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.

Рисунок 1. Дифференциалы простых выражений.

Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:

Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.

Корни уравнений и критические точки

Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.

Источник

Возрастание и убывание функции на интервале, экстремумы

Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.

Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.

Возрастание и убывание функции на интервале

Точки экстремума, экстремумы функции

Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Первое достаточное условие экстремума

Иначе говоря, получим их условия постановки знака:

Алгоритм для нахождения точек экстремума

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

После чего необходимо найти производную:

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

Перейдем к вычислению минимумов:

Произведем вычисления максимумов функции. Получим, что

Второй признак экстремума функции

Для начала находим область определения. Получаем, что

Необходимо продифференцировать функцию, после чего получим

Третье достаточное условие экстремума

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Источник

Возрастание и убывание функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

Разберем примеры решения задач на изучение характера поведения функции.

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли что искали?

Просто напиши и мы поможем

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

То есть функция \(y=5\) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:

Источник