Как доказать что луч это биссектриса угла

Биссектриса угла

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

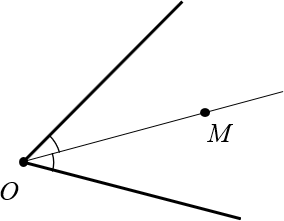
Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

Примеры углов: острый, тупой и прямой

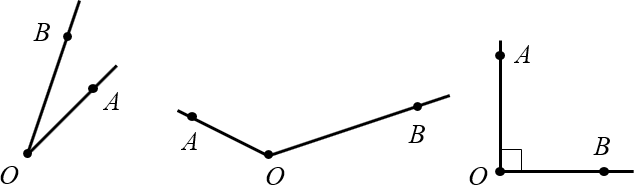
Определение. — это луч, который выходит из вершины этого угла и делит угол пополам.

Для приведённых выше углов биссектрисы будут выглядеть так:

Примеры биссектрис для острого, тупого и прямого угла

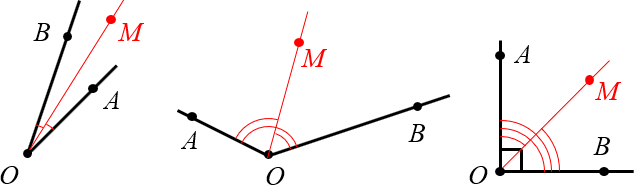
Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. — это длина перпендикуляра, проведённого из данной точки к этой прямой.

Графическое представление расстояния от точки до прямой

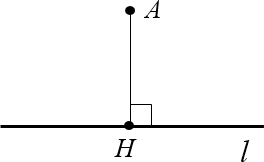
Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

Определяем расстояние от точки до сторон угла

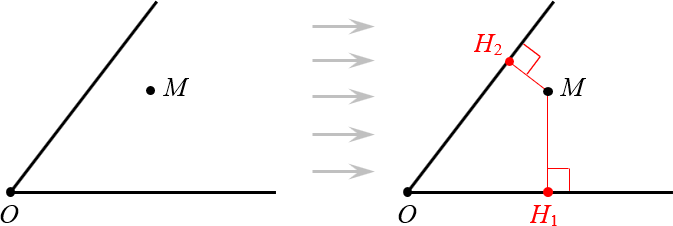
Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

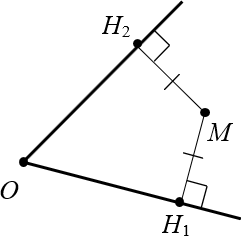
1. Расстояния от точки на биссектрисе до сторон угла одинаковы

Провели перпендикуляры к сторонам угла

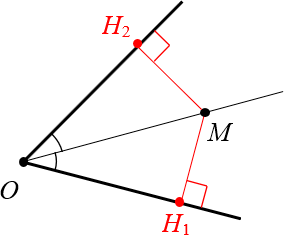
2. Если расстояния равны, то точка лежит на биссектрисе

В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Источник

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Источник

Свойство биссектрисы угла

Теорема

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

Доказательство

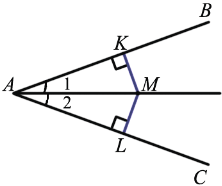
Доказать: MK = ML

Доказательство:

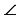
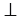
2) Дано: ВАС, MK = ML, МК АВ, MLАС.

Доказательство:

Следствие 1

Следствие 2

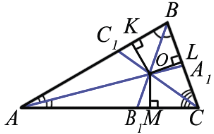
В самом деле, обозначим буквой О точку пересечения биссектрис АА₁ и ВВ₁ треугольника АВС и проведем перпендикуляры ОК, OL и ОМ соответственно к прямым АВ, ВС и СА.

По доказанной теореме ОК = ОМ и ОК = OL. Поэтому ОМ = OL, т.е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе СС₁ этого угла. Следовательно, все три биссектрисы треугольника АВС пересекаются в точке О, что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Источник

Биссектриса угла. Свойства

Определение 1. Биссектриса угла − это луч, исходящий из вершины угла и делящий этот угол в два равных угла.

Докажем следующую теорему:

Теорема 1. 1) Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. 2) Каждая точка, которая находится внутри угла и равноудалена от сторон угла, лежит на его биссектрисе.

2) Пусть точка D лежит внутри угла BAC и равноудалена от его сторон AB и AC. Докажем, что AD является биссектрисей угла BAC (Рис.1). Проведем перпендикуляры DK и DL к прямым AB и AC. Прямоугольные треугольники AKD и ALD равны по катету и гипотенузе. Действительно, гипотенуза AD общая и по условию DK=DL. Но тогда прямоугольные треугольники AKD и ALD равны. Следовательно \( \small ∠1=∠2 \). А это означает, что луч AD является биссектрисей угла BAC.

Исходя из теоремы 1, можно дать другое определение биссектрисы:

Определение 2. Биссектриса угла − это геометрическое место точек внути угла, равноудаленных от сторон этого угла.

Свойство 1. Угол между биссекстрисами смежных углов равна 90°.

Доказательство. Даны смежные углы CAB и BAD (Рис.2). Покажем, что \( \small ∠EAF=90° \) или . Действительно:

Источник

Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком термине, как БИССЕКТРИСА.

Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.

Биссектриса — это.

Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.

Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.

Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:

Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».

Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.

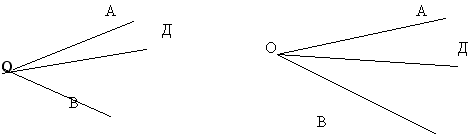
А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.

На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.

Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:

Хотя есть еще вот такие варианты:

Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.

И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.

Количество биссектрис в треугольнике

Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?

Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.

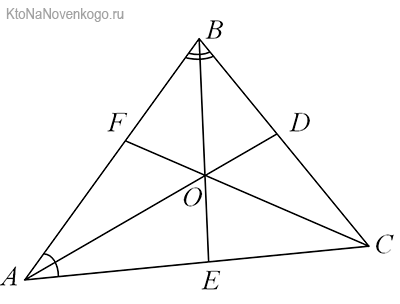
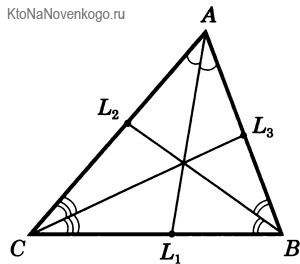
Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.

На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.

То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.

Пересечение биссектрис треугольника

Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:

Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!

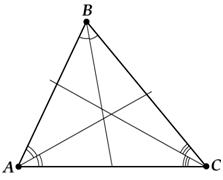
Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:

Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.

А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.

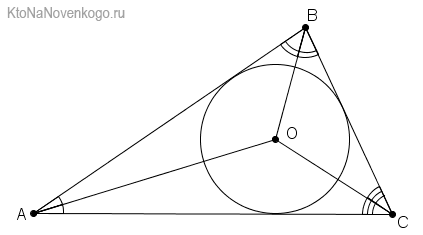
Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.

Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.

Свойство основания биссектрисы

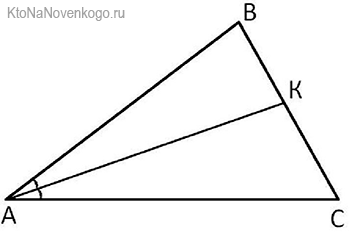
У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.

И с этим основанием связана одна весьма интересная теорема. Она гласит, что

Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.

Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:

Интересно, что для данной теоремы будет справедливо и другое утверждение:

Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.

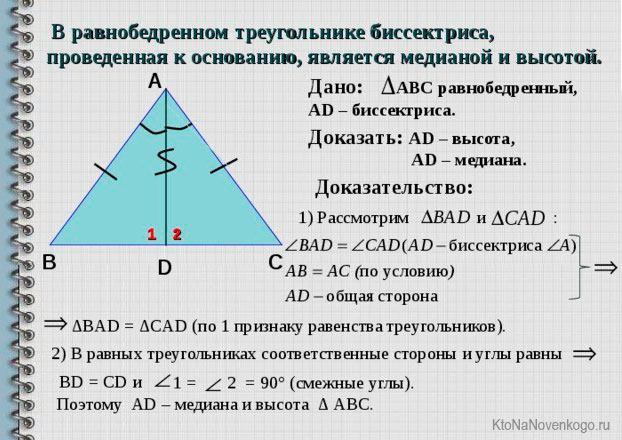
Биссектриса равнобедренного треугольника

Для начала напомним, что такое равнобедренный треугольник.

Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).

Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.

Она одновременно является еще и медианой (что это?), и высотой.

Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:

А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.

Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.

Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.»

Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.

Математика требует точности. Спасибо.

При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.

Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.

Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.

Источник