Как доказать что отрезок является медианой

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Источник

Медиана — это золотое сечение треугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.

У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.

Медиана — это.

Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.

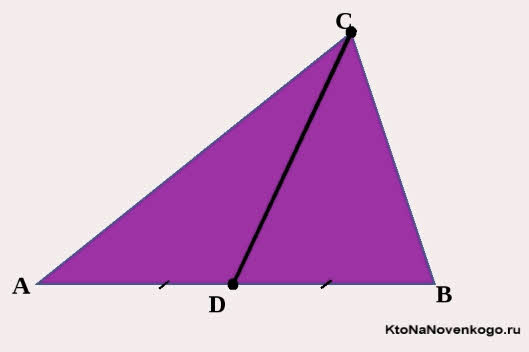
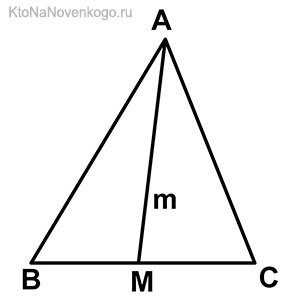
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.

Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.

Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:

Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.

Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.

И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!

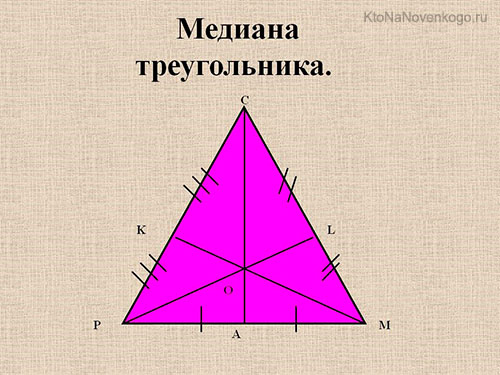
И выглядят они вот так.

На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.

Пересечение медиан треугольника

Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.

Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.

Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.

Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.

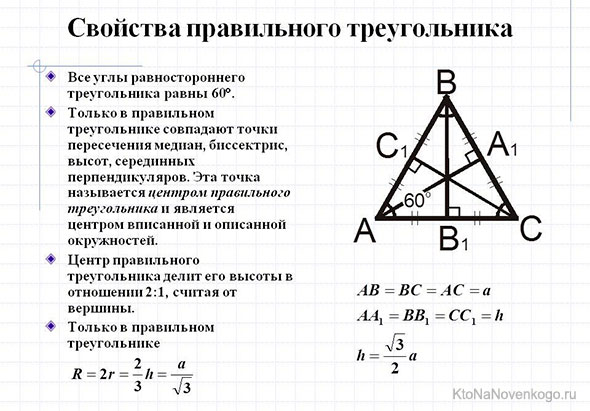
Медиана равностороннего треугольника

Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.

Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.

Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.

И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.

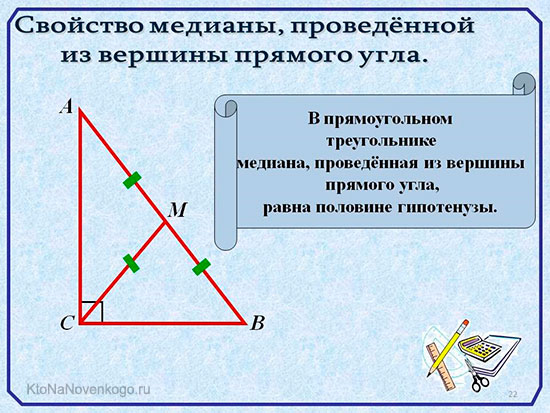
Медиана прямоугольного треугольника

Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.

Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.

Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.

Вместо заключения

А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.

Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.

Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».

И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.

Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Теперь остаётся подумать над тем, как применить это знание о медиане на практике. Если придумаю, вдруг Нобелевскую премию дадут?

Источник

Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса

Свойства медианы треугольника

Итоговое повторение курса геометрии 7 – 9 класса

При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.

Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).

Вспомним некоторые свойства медианы треугольника

Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.

Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что

то, сложив почленно эти три неравенства, получим, что

2AM + BN + CK > AB + BC + AC.

Отсюда следует, что AM + BN + CK > (AB + BC + AC).

Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому

так расположить точки нельзя.

№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10

Решение

Пусть A’B’C’ – треугольник, образованный

проведенными прямыми и G – точка пересечения его

сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и

Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс

Отрабатываем умение: самостоятельно решать задачи.

Свойства медианы. Площадь треугольника

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.

4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).

О т в е т: .

1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.

О т в е т: .

2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.

3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.

4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.

5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.

Медиана, проведенная к гипотенузе

1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.

2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .

3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.

4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

· интернет сайт http://zadachi. ***** Задачи по геометрии

· Всероссийская олимпиада по математике, 2008 год,

· Турнир им. Ломоносова, 2001 год

· Московская математическая регата, 2012/13 г, 8 класс

Источник

Определение и свойства медианы в равнобедренном треугольнике

В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы

Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.

Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.

Свойства медианы в равнобедренном треугольнике

Свойство 1

Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.

Свойство 2

В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.

Свойство 3

Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S₁ = S₂.

Свойство 4

Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S₁ = S₂ = S₃ = S₄ = S₅ = S₆).

Свойство 5

Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:

Свойство 6

Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:

Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

AF = CE, следовательно, AE = EB = BF = FC.

Пример задачи

Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.

Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:

Источник

Треугольник. Важные факты о высоте, биссектрисе и медиане

Определения

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

Доказательство

Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.

Теорема

Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).

Доказательство

Теорема

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.

Доказательство

Теорема

Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:

Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.

Доказательство

Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac>> = \dfrac = \dfrac\]

Теорема

Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.

Доказательство

Источник