Как доказать что прямые параллельны в пространстве

Параллельность прямых, прямой и плоскости и параллельность плоскостей в пространстве

Помнишь, на плоскости была тема «Параллельные прямые»?

Так вот, в пространстве тоже бывают параллельные прямые.

Но… всё немного иначе.

А еще есть параллельность плоскостей – очень важная штука в стереометрии.

Умея с ней работать, становится легче находить углы и значения величин в задачах, выполнять правильные построения.

Читай статью и будешь знать о параллельности плоскостей все!

Параллельность прямых в пространстве

Определение

Прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Обрати внимание! Здесь очень важны слова «лежат в одной плоскости».

Потому что в пространстве бывают другие, НЕ параллельные прямые, которые тоже НЕ пересекаются. Вот, например, такие:

Видишь, через прямые \( \displaystyle a\) и \( \displaystyle b\) никак нельзя провести плоскость, но они и не пересекаются.

Такие прямые называются скрещивающиеся.

Не пересекающиеся! И не параллельные!

Прямые в пространстве параллельны, если лежат в одной плоскости и не пересекаются.

Признаки параллельности прямых в пространстве

Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.

Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.

Пример на признак параллельности прямых в пространстве

Пусть плоскости \( \displaystyle ABDC\) и \( \displaystyle CDFE\).

\( \displaystyle AB\parallel EF\), значит, \( \displaystyle AB\parallel CD\) по признаку параллельности прямых в пространстве.

Параллельность прямой и плоскости

Определение параллельности прямой и плоскости

Прямая и плоскость параллельны, если они не пересекаются, сколько бы их ни продолжали.

Вот так: видишь, прямая как бы «висит» над плоскостью.

И представь себе, существует признак параллельности прямой и плоскости. Давай его сформулируем.

Признак параллельности прямой и плоскости

Прямая \(\displaystyle a \) параллельна плоскости \(\displaystyle \alpha \), если в этой плоскости есть (хоть одна!) прямая \(\displaystyle b \), параллельная \(\displaystyle a \).

Можно сказать и немного другими словами, но смысл остаётся тот же.

Если прямая \(\displaystyle a \) параллельна прямой \(\displaystyle b\), лежащей в плоскости \(\displaystyle \alpha\), то прямая \(\displaystyle a \) параллельна и всей плоскости \(\displaystyle \alpha \).

Пример на признак параллельности прямой и плоскости

Пусть \(\displaystyle SABCD\) – правильная 4 — угольная пирамида.

Тогда, например, \(\displaystyle AB \parallel SCD\). Почему? Но ведь \(\displaystyle AB \parallel CD\), а \(\displaystyle CD \) лежит в плоскости \(\displaystyle SCD\).

Значит (по признаку) \(\displaystyle AB \parallel SCD\).

Параллельность плоскостей

Определение параллельности плоскостей

Плоскости называются параллельными, если они не пересекаются, сколько бы их не продолжали

И так же, как для прямой и плоскости, есть признак параллельности плоскостей. Его формулировка немного длиннее.

Признак параллельности двух плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Параллельность в пространстве: свойство транзитивности

Ух, ну и название! О чём же мы?

А вот ты задумайся над вопросом: правда ли, что если прямая \( \displaystyle a \) параллельна прямой \( \displaystyle b\), a \( \displaystyle b \parallel c\), то \( \displaystyle a \parallel c\)?

И есть ответ: правда! И как раз такой перенос с “\( \displaystyle a\)” через “\( \displaystyle b\)” на “\( \displaystyle c\)” и называется «транзитивность».

Давай-ка теперь рассмотрим несколько вариантов в буквах и картинках:

\( \displaystyle a \parallel b\) и \( \displaystyle b \parallel c \Rightarrow a \parallel c\).

\( \displaystyle \alpha \parallel \beta\) и \( \displaystyle \beta \parallel \gamma \Rightarrow \alpha \parallel \gamma\).

\( \displaystyle a\parallel \alpha\quad\) и \( \displaystyle \quad \alpha\parallel \beta\Rightarrow a\parallel \beta\).

\( \displaystyle \alpha \parallel b\quad\) и \( \displaystyle\quad b\parallel \alpha \Rightarrow text\parallel \alpha \)

И один неверный вариант:

\( \displaystyle a\parallel \alpha \) и \( \displaystyle \alpha \parallel b\) \( \displaystyle НЕ \Rightarrow \) \( \displaystyle a\parallel b\).

Ну вот, мы обсудили определения и признаки параллельности прямых и плоскостей и даже немножко порисовали транзитивности. Давай теперь рассмотрим несколько примеров.

Пример на признак параллельности плоскостей

Пусть в пирамиде \( \displaystyle SABC\) проведена плоскость \( \displaystyle MNK\) через середины рёбер \( \displaystyle SA\), \( \displaystyle SB\) и \( \displaystyle SC\).

Тогда \( \displaystyle MNK\parallel ABC\). Почему?

Да просто \( \displaystyle MN\parallel AB\) (средняя линия), \( \displaystyle NK\parallel BC\) (тоже средняя линия, но в \( \displaystyle \Delta SBC\)).

Значит, получилось, что \( \displaystyle MN\) и \( \displaystyle NK\) – пересекающиеся прямые в одной плоскости соответственно параллельны \( \displaystyle AB\) и \( \displaystyle BC\) – пересекающимся прямым в другой плоскости – работает признак \( \displaystyle \Rightarrow \) \( \displaystyle MNK\parallel ABC\).

Источник

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

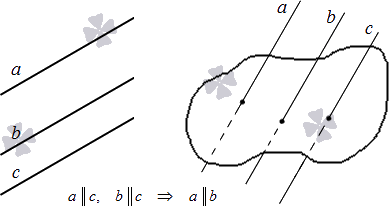
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

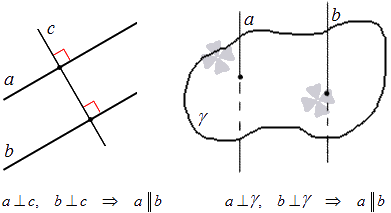
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

Определение параллельных прямых в пространстве

Понятие о параллельных прямых

Прямые \(a\) и \(b\) являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются.

Если рассмотреть примеры, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочее. Таких примеров из реального мира можно привести очень много.

Другими вариантами прямых, расположенных в 3D-пространстве, есть их скрещивание и пересечение. Пересекающимися есть прямые, имеющие общую точку, она же и есть точкой пересечения. Скрещивающимися есть прямые, расположенные в разных плоскостях и не параллельные между собой.

Есть ряд теорем, описывающих поведение параллельных прямых в пространстве. Рассмотрим их подробнее.

Теоремы о параллельности двух прямых

Свойства параллельных прямых в пространстве

Некоторые свойства пересекаются с вышеизложенными теоремами, но все же рассмотрим их все:

Не нашли что искали?

Просто напиши и мы поможем

В соответствии с аксиомой планиметрии, при пересечении одной из параллельных прямых третьей прямой, вторая так же будет ее пересекать.

Пример задачи о параллельных прямых

При совпадении прямых или если они параллельны их направляющие векторы \(s_1\) и \( s_2\) будут коллинеарными, таким образом, их координаты будут иметь следующее соотношение:

Для того, чтобы найти направляющие вектора, воспользуемся каноническими уравнениями, таким образом для прямой a вектор \(s_1\) будет равен <1;3;-2>.

Для прямой b найдем направляющий вектор при помощи произведения нормальных векторов плоскостей, на которых он расположен:

Таким образом, соблюдается вышеуказанное условие, значит эти прямые либо параллельны, либо совпадают. Необходимо определить каковыми именно они являются: параллельны или совпадают. Возьмем некую точку \(K\) с координатами (1;2;-1), находящуюся на прямой a, и подставим ее координаты в уравнение прямой \(b\) :
1-2+1+1=0;1=0,

Источник

Стереометрия. Страница 2

Главная > Учебные материалы > Математика: Стереометрия. Страница 2

1.Параллельность прямых в пространстве. 2.Признак параллельности прямых. 3.Признак параллельности плоскостей. 4.Свойства параллельных плоскостей. 5.Примеры.

1. Параллельность прямых в пространстве

Теорема. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Доказательство. Пусть b данная прямая и точка А, не лежащая на данной прямой. Проведем через точку А и прямую b плоскость α. А через точку А прямую a, параллельную прямой b. (Рис.1)

Допустим, что существует другая прямая а’, параллельная прямой b и проходящая через точку А. Тогда через них можно провести плоскость β. Отсюда следует, что через точку А и прямую b можно провести две плоскости. А это невозможно согласно теореме о единственности существования плоскости, проведеной через прямую и не лежащую на ней точку. Таким образом, плоскости α и β совпадают. А следовательно, согласно аксиоме, прямые а и a’ совпадают также.

Рис. 1 Параллельность прямых в пространстве.

2.Признак параллельности прямых

Теорема. Две прямые, параллельные третьей прямой, параллельны.

Доказательство. Пусть прямые а и b лежат в разных плоскостях и параллельны прямой с. Доказать, что прямые а и b параллельны между собой. (Рис.2)

Рис.2 Признак параллельности прямых

3. Признак параллельности плоскостей

Теорема: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Доказательство.

а ∈ α, γ.
а 1 ∈ β, γ.
с ∈ α, β,γ

т.е. плоскости α и γ пересекаются по двум прямым а и с, а плоскости β и γ пересекаются по прямым а 1 и с.

Рис. 3 Признак параллельности плоскостей.

Согласно аксиоме стереометрии, это невозможно, т.к. две плоскости могут пересекаться только по одной прямой. И следовательно, наше предположение неверно. Плоскости α и β не пересекаются, они параллельны.

4. Свойства параллельных плоскостей

Теорема: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

Доказательство.

Пусть даны две параллельные плоскости α и β (Рис.4). Плоскость γ пересекает их по прямым а и b.

Рис. 4 Свойства параллельных плоскостей.

5. Пример 1

Докажите, что если прямые АВ и CD скрещивающиеся, то прямые АС и BD тоже скрещиваются.

Доказательство:

Пусть даны две скрещивающиеся прямые АВ и CD. Проведем через прямую АВ и точку С плоскость α (Рис.5). Так как прямые АВ и CD скрещивающиеся, то прямая CD не лежит в плоскости α, а пересекает ее в одной точке С.

Отсюда следует, что точка D не принадлежит плоскости α. Она лежит вне ее.

Таким образом, если мы проведем прямую АС, то она полностью будет принадлежать плоскости α, так как две ее точки А и С принадлежат плоскости α.

А прямая BD не будет принадлежать плоскости α, так как точка D не принадлежит плоскости α. Прямая BD будет пересекать плоскость α в одной точке В.

Отсюда можно сделать вывод, что прямая АС не может пересекать прямую BD, так как прямая АС полностью принадлежит плоскости α. А прямая BD имеет только одну общую точку с плоскостью α, точку В. Но так как точка В не лежит на прямой АС, следовательно, прямые АС и BD не пересекаются. Они являются скрещивающимися.

Рис.5 Задача. Докажите, что если прямые АВ и CD скрещивающиеся.

Пример 2

Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем плоскость α через точки A, D, C и плосксоть α’ через точки А, В, С (Рис.6). Точки P, S, F, E являются серединами отрезков AB, BC, AD и CD соответственно. Необходимо доказать, что прямая PS параллельна прямой FE.

Рассмотрим треугольник АВС. Он полностью лежит в плоскости α’, так как три его вершины лежат в данной плоскости по построению. Отрезок PS представляет собой среднюю линию треугольника, которая параллельна АС.

Теперь рассмотрим треугольник АСD. Он полностью лежит в плоскости α, так как три его вершины лежат в данной плоскости по построению. Отрезок FE представляет собой среднюю линию треугольника, которая также параллельна АС.

Отсюда можно сделать вывод: если две прямые PS и FE параллельны третьей прямой АС, то они параллельны и между собой. И равны половине основанию АС. Таким образом, PSEF представляет собой параллелограмм.

Рис.6 Задача. Точки А, В, С, D не лежат в одной плоскости.

Пример 3

Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и ВС, АС и BD, AD и BC пересекаются в одной точке.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем отрезки EP, VS, FT, которые соединят середины сторон AB и CD, BC и AD, AC и BD соответственно (Рис.7).

Из предыдущей задачи нам известно, что четырехугольник EVPS, вершины которого являются серединами отрезков АВ, ВС, СD и AD, есть параллелограмм, у которого EP и VS диагонали. Эти диагонали пересекаются в точке О и делятся этой точкой пополам.

Так как у отрезка VS середина одна, т.е. точка О, то все три диагонали EP, VS и FT пересекаются в этой точке.

Рис.7 Задача. Даны четыре точки А, В, С, D, не лежащие в одной плоскости.

Пример 4

Докажите, что если две плоскости, пересекающиеся по прямой а, пересекают плоскость α по параллельным прямым, то прямая а параллельна плоскости α.

Доказательство:

Пусть даны две плоскости β и γ, пересекающиеся по прямой а (Рис.8). Эти плоскости пересекают плоскость α по параллельным прямым b и с. Необходимо доказать, что прямая а параллельна плоскости α.

Рис.8 Задача. Докажите, что если две плоскости, пересекающиеся по прямой а.

Пример 5

Докажите, что если четыре прямые, проходящие через точку О, пересекают плоскость α в вершинах параллелограмма, то они пересекают любую плоскость, параллельную α и не проходящую через точку О, тоже в вершинах параллелограмма.

Доказательство:

Пусть даны четыре прямые, проходящие через точку О, ОА, ОВ, ОС и OD (Рис.9). Они пересекают плоскость α в точках А, В, С и D соответственно. Проведем плоскость α’, параллельную плоскости α. Тогда прямые ОА, ОВ, ОС и OD пересекут плоскость α’ в точках A’B’C’D’.

Проведем плоскость β через точки А, В, A’, B’. Тогда прямые АВ и A’B’ не пересекаются, так как это прямые пересечения двух параллельных плоскостей α и α’ с секущей плоскостью β.

Отсюда следует, что прямые ВС и В’С’, CD и C’D’, AD и A’D’ параллельны. А так как АВ параллельна CD, а ВС параллельна AD, то следовательно, А’В’ параллельна C’D’, а В’С’ параллельна A’D’.

Таким образом, A’B’C’D’ также является параллелограммом.

Рис.9 Задача. Докажите, что если четыре прямые, проходящие через точку А.

Источник