Как доказать что прямые совпадают

Вывести условия параллельности, совпадения и перпендикулярности прямых на плоскости

Условие параллельности двух прямых (вывод):

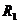
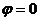
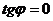
а) Если прямые и заданы уравнениями с угловым коэффициентом и параллельны, то . Тогда и из формулы

или . Таким образом, достаточное условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е. .

Условия перпендикулярности двух прямых (вывод):

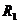
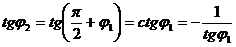
а) Если прямые и заданы уравнениями с угловым коэффициентом и перпендикулярны, то . Так как , то и , т.е. .

, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A₁A₂ + B₁B₂ = 0.

Условие совпадение двух прямых

На плоскости заданы прямые 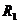, общими уравнениями: _{; . (1)}

Очевидно, совпадение двух прямых есть частный случай параллельности. Поэтому должно быть О _(2). Обозначая общую величину обоих отношений через , имеем _{, (3),}

Откуда _{, .} Тогда уравнение системы (1) имеет вид _, или _. Если уравнения (1) изображают одну и ту же прямую, то одни и те же координаты х, y удовлетворяют как уравнению (4), так и второму уравнению системы (1). Поэтому, если вычтем из уравнения (4) второе уравнение (1), то получим или _. Сопоставляя это с (3), находим _. Это и есть условие совпадения двух прямых, которое говорит о том, что коэффициенты совпадающих прямых пропорциональны, то есть одно уравнение получается из второго путем умножения на некоторое постоянное число (число )

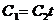
2. Производная: физические задачи, приводящие к понятию производной, определение.

физические задачи, приводящие к понятию производной

Задача о скорости движущейся точки.

Пусть s = s (t) представляет закон прямолинейного движения материальной точки.

Это уравнение выражает путь s, пройденный точкой, как функцию времени t.

Чем меньше Δt, т. е. чем короче промежуток времени от t до t + Δt, тем лучше средняя скорость характеризует движение точки в момент времени t. Поэтому естественно ввести понятие скорости v в данный момент t, определив ее как предел средней скорости за промежуток от t до t + Δt, когда :

Величина v называется мгновенной скоростью точки в данный момент t.

Задача о касательной к данной кривой.

Пусть на плоскости хОу дана кривая уравнением у = f (х). Требуется провести касательную к данной кривой в данной точке .

Так как точка касания 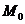д ана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. — тангенс угла наклона касательной к положительному направлению оси Ох (рис.).
Через точки и проведем секущую

Из рис. видно, что угловой коэффициент секущей равен отношению , где .

Угловой коэффициент касательной к данной кривой в точке можно найти на основании следующего определения: касательной к кривой в точке называется прямая , угловой коэффициент которой равен пределу углового коэффициента секущей , когда . Отсюда следует, что
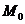
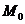
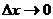
Производной функции f(x) в точке х=х₀ называется отношение приращения функции 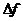в этой точке к приращению аргумента, при стремлении последнего к нулю.

_при

Дата добавления: 2018-04-05 ; просмотров: 1813 ; Мы поможем в написании вашей работы!

Источник

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник