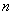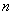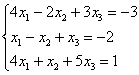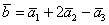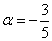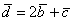Как доказать что система векторов является базисом
Доказать, что каждая из двух заданных систем векторов..
Задание:
Доказать, что каждая из двух заданных систем векторов S и S’ является базисом. Найти матрицу перехода от S к S’.
Решение:
1) Чтобы доказать, что эти системы векторов являются базисом, докажем, что они линейно независимы. Для этого введем обозначения
(1,1,1,1) = e1, (1,2,1,1) = e2, (1,1,2,1) = e3, (1,3,2,3) = e4.
(1,0,3,3) = f1, (-2,-3,-5,-4) = f2, (2,2,5,4) = f3, (-2,-3,-4,-4) = f4.
Запишем систему для первой системы и решим ее методом Гаусса:
Видим, что система векторов (e1,e2,e3,e4) линейно независима. Можно также посчитать определитель матрицы и убедиться, что он не равен нулю, а следовательно по методу Крамера существует одно единственное решение и оно нулевое, как видно из системы.
Запишем систему и приведем ее к единичной слева, а справа получим матрицу перехода.
Ответ:
Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе
Даны векторы 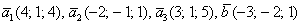
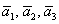
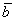
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора 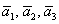
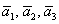
Вычислим определитель, составленный из координат векторов 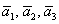
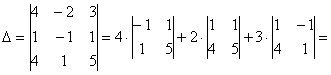
! Важно: координаты векторов 
Теперь вспомним теоретическую часть: если векторы 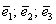
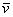
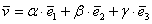
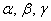
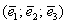
Поскольку наши векторы 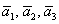
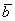
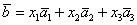
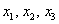
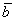
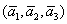
По условию и требуется найти координаты 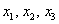
Для удобства объяснения поменяю части местами: 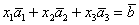
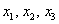
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя 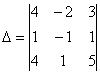
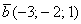
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден:
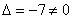
Дальнейшее – дело техники:
Таким образом:
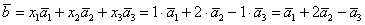
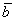
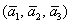
Ответ:
Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы 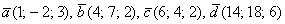
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: составим пропорцию из соответствующих координат векторов:
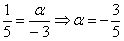
Ответ: при
Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон 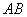
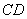
Найдём векторы:
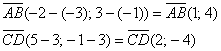
Вычислим определитель, составленный из координат векторов 
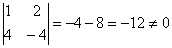
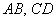
2) Проверим параллельность противоположных сторон 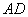
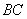
Найдём векторы:
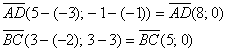
Вычислим определитель, составленный из координат векторов 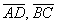
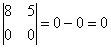
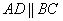
Вывод: Две стороны четырёхугольника 
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
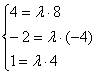
Система не имеет решения, значит, векторы 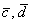
Более простое оформление:
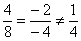
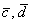
Ответ: векторы 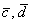
в) Исследуем на коллинеарность векторы 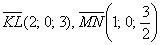
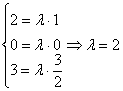
Соответствующие координаты векторов пропорциональны, значит 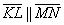
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов 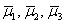
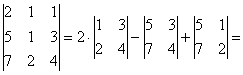
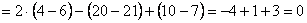
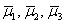
Ответ: данные векторы не образуют базиса
Пример 9:Решение:Вычислим определитель, составленный из координат векторов 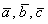

Таким образом, векторы 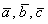
Представим вектор 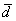
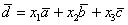
Покоординатно:
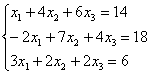
Систему решим по формулам Крамера:
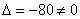
Ответ: Векторы 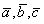
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урокаВекторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
11. Базис множества векторов и всего линейного пространства
Система векторов 


Все векторы системы 

Система векторов 
Любой вектор 


Если множество 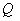


Числа 





Теорема (о единственности разложения по данному базису).
Разложение любого вектора 

Доказательство. Предположим, что для вектора 



Поскольку базисные векторы линейно независимы, то из полученного равенства следуют равенства 
Следствие. Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.
Таким образом, при фиксированном базисе линейного пространства каждый вектор однозначно определяется своими координатами в этом базисе.
Теорема (о линейных свойствах координат векторов).
При сложении любых двух векторов их координаты в данном базисе складываются, а при умножении любого вектора на любое число координаты умножаются на это число.
Доказательство. Пусть любые два вектора 





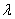


Отсюда и теоремы о единственности разложения векторов по данному базису следует истинность доказываемой теоремы.
Теорема о базисном миноре.
Базисные строки (столбцы) линейно независимы и образуют базис в системе всех строк (столбцов) произвольной матрицы 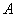
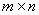
По определению базиса это означает, что любая строка или столбец матрицы могут быть представлены в виде линейной комбинации базисных строк или базисных столбцов, причем единственным образом. Все рассуждения достаточно провести для строк, так как, транспонировав исходную матрицу, мы получим доказательство для столбцов матрицы 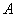
Линейную независимость базисных строк будем доказывать методом от обратного.
Пусть некоторые базисные строки линейно зависимы. Тогда одна из этих строк является линейной комбинацией остальных строк. Но тогда из свойств определителей следует, что базисный минор равен нулю. Базисный минор по определению не должен быть равен нулю. Таким образом, исходное предположение ложно и базисные строки линейно независимы.
Докажем теперь, что любая строка произвольной матрицы 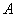
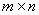
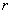
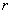
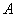
Пусть 
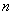
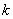
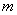

Равен нулю. Если 



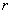




Алгебраические дополнения к элементам последнего столбца с номером 






Эти равенства справедливы для любых чисел 


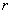
Из теоремы о базисном миноре вытекают два важных следствия.
1. Для любой матрицы число линейно независимых строк равно числу линейно независимых столбцов и равно рангу матрицы.
2. Определитель любого порядка равен нулю тогда и только тогда, когда его строки или его столбцы линейно зависимы.
Отметим, что по закону контрпозиции равносильное свойству 2 утверждение формулируется следующим образом: определитель отличен от нуля тогда и только тогда, когда его строки или его столбцы линейно независимы.
Покажем достаточность условия второго следствия. Если строки матрицы линейно зависимы, то по свойству системы зависимых векторов одна из строк является линейной комбинацией остальных строк. Вычитая из этой строки указанную линейную комбинацию, мы, не изменяя величины определителя, получим матрицу, содержащую нулевую строку. Определитель такой матрицы всегда равен нулю, что и требовалось доказать.
Покажем, что условие линейной зависимости столбцов квадратной матрицы является необходимым для равенства нулю определителя матрицы. Если определитель порядка