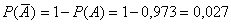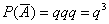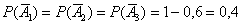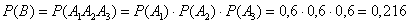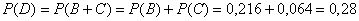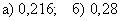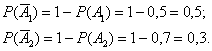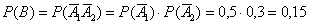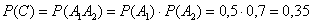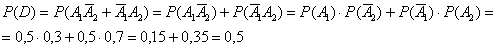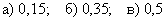Как доказать что события независимы

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №34. Условная вероятность. Независимость событий.

Перечень вопросов, рассматриваемых в теме:

— Совместные и несовместные события

— Схема решения задач на вычисление условной вероятности события;

— Задачи на определение независимости событий.

Совместные события – события, одновременное появление которых возможно.

Несовместные события – события, одновременное появление которых невозможно.

События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.

Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается P_A(B).

Условная вероятность – вероятность наступления одного события при условии, что другое событие уже произошло.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 186-194.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе.

Рассмотрим примерную задачу:

Из колоды карт извлекают четыре карты. Первые две оказались семёрками. Какова вероятность, что одна или обе оставшиеся карты окажутся семёрками? (колода содержит 36 карт)

События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример совместных событий: выпадение чётного числа и выпадение числа, кратного трём, при броске игрального кубика. Когда выпадает шесть, реализуются сразу оба события.

События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

Пример несовместных событий: выпадение чётного числа и выпадение нечётного числа при броске игрального кубика.

Теорема о сумме двух событий:

Вероятность суммы любых двух событий А и В равна сумме вероятностей этих событий без вероятности их совместного осуществления: Р(А+В) = Р(А)+Р(В)-Р(АВ)

В лотерее выпущено 10 000 билетов, из них: 10 выигрышей по 200 рублей, 100 выигрышей по 100 рублей, 500 выигрышей по 50 рублей и 1000 выигрышей по 10 рублей. Какова вероятность того, что человек, купивший билет, выиграет не менее 50 рублей?

Воспользуемся теоремой: Р(М)=Р(А)+Р(В)+Р(С)=0,061.

Дана вероятность исходного события. Чему равна вероятность противоположного события?

Вероятность исходного события А обозначим Р(А). Вероятность противоположного события Р(Ᾱ).

События А и Ᾱ образуют полную группу событий, вероятность которой равна 1.

Тогда вероятность противоположного события находится по формуле:

Например, монета брошена два раза.

Вероятность появления «Орла» во втором испытании не зависит от результата первого испытания.

Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:

Подбрасываются две монеты. Найдите вероятность выпадения двух орлов.

Введем обозначение событий:

A₁– на 1-й монете выпадет орёл;

A₂– на 2-й монете выпадет орёл.

Событие “выпадение двух орлов” заключается в том, что на 1-й монете появится орёл и на 2-й монете появится орёл, следовательно, это произведение событий A₁A₂. Вероятность выпадения орла на одной монете не зависит от результата броска другой монеты, следовательно, события A₁ и A₂ независимы. По теореме умножения вероятностей независимых событий получим:

Отыскать вероятность совместного появления зависимых событий помогает теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: P(AB) = P(A)·P_A(B).

Связь теории вероятностей с теорией множеств.

В математике принято устанавливать связи между различными разделами. Связь между теорией вероятностей и теорией множеств устанавливается следующим образом: события отождествляются с множествами. В таком случае понятию исход будет эквивалентно понятие элемент множества. При таком подходе выберите из списка, какому понятию из теории множеств соответствует данное понятие из теории вероятностей:

— Невозможное событие (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)

— Сумма событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)

— Произведение событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)

Примеры и разбор решения заданий тренировочного модуля

1. В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара без возврата. Найдите вероятность того, что первый шар окажется черным, второй – красным и третий – белым.

А – первый шар окажется черным

.

2. Колю отпускают гулять при условии сделанных уроков с вероятностью 0,8. Папа выдает ему деньги на мороженое с вероятностью 0,6. С какой вероятностью Коля пойдет гулять без мороженого?

A – папа выдал Коле денег на мороженое

B – Колю отпустили гулять

Вероятность того, что Коля пойдёт гулять, есть в условии задачи P(B) = 0,8. Вероятность, что папа не выдаст ему деньги на мороженое, равна P(Ᾱ) = 1 – P(A) = 1 – 0,6 = 0,4. Вероятность одновременного осуществления двух независимых событий – произведение их вероятностей P(ᾹB) = P(Ᾱ)·P(B) = 0,8·0,4 = 0,32.

Источник

Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей

Теоремы сложения вероятностей

Найдем вероятность суммы событий и (в предположении их совместности либо несовместности).

Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:

Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.

Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.

Решение. События «очередной будет продана пара обуви меньше 44-го размера» и «будет продана пара обуви размера не меньше 44-го» противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события

Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).

Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:

Зависимые и независимые события. Условная вероятность

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие ) не зависит от появления или не появления «герба» во втором испытании (событие ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Формулы умножения вероятностей

Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие ) и при третьем — синий (событие ).

Формула полной вероятности

При этом события называются гипотезами, а вероятности — априорными. Эта формула называется формулой полной вероятности.

Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.

Формула Байеса

Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем

Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.

Решение. Рассчитаем условные вероятности по формуле Байеса:

Источник

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Источник

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Источник

Как определить зависимость/независимость событий?

Иногда об этом прямо сказано в условии задачи, но чаще всего приходится проводить самостоятельный анализ. Какого-то однозначного ориентира тут нет, и факт зависимости либо независимости событий вытекает из естественных логических рассуждений.

Чтобы не валить всё в одну кучу, задачам на зависимые события я выделю следующий урок, а пока мы рассмотрим наиболее распространённую на практике связку теорем:

Задачи на теоремы сложения вероятностей несовместных
и умножения вероятностей независимых событий

Этот тандем, по моей субъективной оценке, работает примерно в 80% задач по рассматриваемой теме. Хит хитов и самая настоящая классика теории вероятностей:

Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Найти вероятность того, что:

а) только один стрелок попадёт в мишень;
б) хотя бы один из стрелков попадёт в мишень.

Решение: вероятность попадания/промаха одного стрелка, очевидно, не зависит от результативности другого стрелка.

Рассмотрим события: А₁ – 1-й стрелок попадёт в мишень;

А₂ – 2-й стрелок попадёт в мишень.

Найдём вероятности противоположных событий – того, что соответствующие стрелки промахнутся:

а) Рассмотрим событие: В – только один стрелок попадёт в мишень. Данное событие состоит в двух несовместных исходах:

1-й стрелок попадёт и2-й промахнётся
или
1-й промахнётся и 2-й попадёт.

На языке алгебры событий этот факт запишется следующей формулой: В = +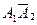

Сначала используем теорему сложения вероятностей несовместных событий, затем – теорему умножения вероятностей независимых событий:

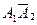
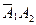
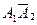
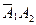
Р(В) =Р( + ) = + Р( ) + Р( ) = Р( ) × Р( ) +Р( ) × Р( ) =

= 0,8 × 0,4 + 0,2 × 0,6 = 0,32 + 0,12 = 0,44 – вероятность того, что будет только одно попадание.

б) Рассмотрим событие: С – хотя бы один из стрелков попадёт в мишень.

Прежде всего, ВДУМАЕМСЯ – что значит условие «ХОТЯ БЫ ОДИН»? В данном случае это означает, что попадёт или 1-й стрелок (2-й промахнётся) или 2-й (1-й промахнётся) или оба стрелка сразу – итого 3 несовместных исхода.

Способ первый: учитывая готовую вероятность предыдущего пункта, событие удобно представить в виде суммы следующих несовместных событий:

попадёт кто-то один (событие В, состоящее в свою очередь из 2-х несовместных исходов) или
попадут оба стрелка – обозначим данное событие буквой D.

Таким образом: C = B + D.

По теореме умножения вероятностей независимых событий:

P (D) = P(А₁ А₂) = P(А₁) × P(А₂) = 0,8 × 0,6 = 0,48 – вероятность того, что 1-й стрелок попадёт и 2-ой стрелок попадёт.

По теореме сложения вероятностей несовместных событий:

Р(C) = Р(B + D) = Р( B) + Р( D) = 0,44 + 0,48 = 0,92. – вероятность хотя бы одного попадания по мишени.

Способ второй: рассмотрим противоположное событие: – оба стрелка промахнутся.

По теореме умножения вероятностей независимых событий:

Р( ) = Р ( ) = Р ( ) × Р ( ) = 0,2 × 0,4 = 0,08.

В результате: Р(С) = 1 – Р( ) = 1 – 0,08 = 0,92.

Особое внимание обратите на второй способ – в общем случае он более рационален.

Кроме того, существует альтернативный, третий путь решения, основанный на теореме, которая будет рассмотрена на следующем уроке: теореме сложения совместных событий.

!Если вы знакомитесь с материалом впервые, то во избежание путаницы, следующий абзац лучше пропустить.

Способ третий: события А₁ и А₂ совместны, а значит, их сумма А₁ + А₂ выражает событие «хотя бы один стрелок попадёт в мишень» (см. алгебру событий). По теореме сложения вероятностей совместных событий и теореме умножения вероятностей независимых событий:

Выполним проверку: события , В и D (0, 1 и 2 попадания соответственно) образуют полную группу, поэтому сумма их вероятностей должна равняться единице:

Р( ) + Р(В) + Р(D) = 0,08 + 0,44 + 0,48 = 1, что и требовалось проверить.

Ответ: а) вероятность того, что только один стрелок попадёт в мишень, равна 0,44,

б) вероятность того, что хотя бы один из стрелков попадёт в мишень, равна 0,92

На практике можно пользоваться любым вариантом оформления. Конечно же, намного чаще идут коротким путём, но не нужно забывать и 1-й способ – он хоть и длиннее, но зато содержательнее – в нём понятнее, что, почему и зачем складывается и умножается.

Задача 6 для самостоятельного решения

Для сигнализации о возгорании установлены два независимо работающих дат­чика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре:

а) оба датчика откажут;
б) оба датчика сработают.
в) Пользуясь теоремой сложения вероятностей событий, образующих полную группу, найти вероятность того, что при пожаре сработает только один датчик. Проверить результат прямым вычислением этой вероятности (с помощью теорем сложения и умножения).

Здесь независимость работы устройств непосредственно прописана в условии, что, кстати, является важным уточнением. Образец решения оформлен в академичном стиле.

Как быть, если в похожей задаче даны одинаковые вероятности, например, 0,9 и 0,9? Решать нужно точно так же!

Стрелок попадает в цель с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность хотя бы одного попадания при трех выстрелах равна 0,973.

Решение: обозначим через – вероятность попадания в мишень при каждом выстреле.
и через – вероятность промаха при каждом выстреле.

И таки распишем события:
– при 3-х выстрелах стрелок попадёт в мишень хотя бы один раз;
– стрелок 3 раза промахнётся.

По условию , тогда вероятность противоположного события:

С другой стороны, по теореме умножения вероятностей независимых событий:

Таким образом:

– вероятность промаха при каждом выстреле.

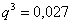
В результате:
– вероятность попадания при каждом выстреле.

Ответ: 0,7

Задача 2: В коробке 10 красных и 6 синих пуговиц. Наудачу извлекаются две пуговицы. Какова вероятность того, что они будут одноцветными?

Решение:всего: 10 + 6 = 16 пуговиц в коробке.
способами можно извлечь 2 пуговицы из коробки;
способами можно извлечь 2 красные пуговицы;
способами можно извлечь 2 синие пуговицы.
По классическому определению:
– вероятность того, что из коробки будут извлечены две красные пуговицы;
– вероятность того, что из коробки будут извлечены две синие пуговицы.
По теореме сложения вероятностей несовместных событий:
– вероятность того, что из коробки будут извлечены две одноцветные пуговицы.
Ответ: 0,5

Задача 4: В трех урнах имеется по 6 белых и по 4 черных шара. Из каждой урны извлекают наудачу по одному шару. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета.

Решение: рассмотрим события: – из 1-й, 2-й и 3-й урны соответственно будет извлечён белый шар. По классическому определению вероятности:

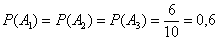
Тогда вероятности извлечения чёрного шара из соответствующих урн равны:

а) Рассмотрим событие: – из каждой урны будет извлечено по 1-му белому шару.
Данное событие выражается в виде произведения (из 1-й урны будет извлечён БШ и из 2-ой урны будет извлечён БШ и из 3-й урны будет извлечён БШ).
По теореме умножения вероятностей независимых событий:

б) Рассмотрим событие – из каждой урны будет извлечено по 1-му чёрному шару.
По теореме умножения вероятностей независимых событий:

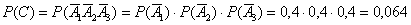
Рассмотрим событие – все три шара будут одного цвета. Данное событие состоит в двух несовместных исходах: (будут извлечены 3 белых или 3 чёрных шара)
По теореме сложения вероятностей несовместных событий:

Ответ:

Задача 6: Для сигнализации о возгорании установлены два независимо работающих дат­чика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре:

Решение:рассмотрим следующие события:
– при возгорании сработает 1-й датчик;
– при возгорании сработает 2-й датчик.
По условию: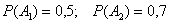
Вычислим вероятности противоположных событий:

а) Рассмотрим событие: – при пожаре оба датчика откажут.
По теореме умножения вероятностей независимых событий:

б) Рассмотрим событие: – при пожаре оба датчика сработают.
По теореме умножения вероятностей независимых событий:

в) Рассмотрим событие: – при пожаре сработает только один датчик.
События образуют полную группу, следовательно:

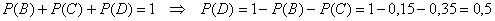
Проверим результат с помощью прямого вычисления. Событие состоит в 2-х несовместных исходах: 1-й датчик сработает и 2-й откажет или 1-ый откажет и 2-й сработает. Таким образом: .
По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

Ответ:

Источник