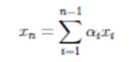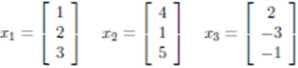Как доказать что столбцы матрицы линейно зависимы

Линейная независимость

Каждую строку матрицы А обозначим е_i = (a_i1 a_i2 …, a_in) (например,
е₁ = (a₁₁ a₁₂ …, a_1n), е₂ = (a₂₁ a₂₂ …, a_2n) и т.д.). Каждая из них представляет собой матрицу-строку, которую можно умножить на число или сложить с другой строкой по общим правилам действий с матрицами.

Строки матрицы e_l, e₂. e_m называются линейно зависимыми, если существуют такие числа l_l, l₂. l_m, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
l_le_l + l₂e₂ +. + l_me_m = 0, где 0 = (0 0. 0).

Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Действительно, пусть для определенности последний коэффициент l_m ¹ 0. Тогда, разделив обе части равенства на l_m, получим выражение для последней строки, как линейной комбинации остальных строк:
e_m = (l_l/l_m)e_l + (l₂/l_m )e₂ +. + (l_m-1/l_m)e_m-1.

Если линейная комбинация строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю, т.е. l_le_l + l₂e₂ +. + l_me_m = 0 Û l_k = 0 «k, то строки называют линейно независимыми.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые можно линейно выразить все остальные ее строки или столбцы.

Докажем эту теорему. Пусть матрица А размера m х n имеет ранг r (r(А) £ min ). Следовательно, существует отличный от нуля минор r-го порядка. Всякий такой минор будем называть базисным. Пусть для определенности это минор

Строки этого минора также будем называть базисными.

Докажем, что тогда строки матрицы e_l, e₂. e_r линейно независимы. Предположим противное, т.е. одна из этих строк, например r-я, является линейной комбинацией остальных: e_r = l_le_l + l₂e₂ +. + l_r-1e_r-1 = 0. Тогда, если вычесть из элементов r-й строки элементы 1-й строки, умноженные на l_l, элементы 2-й строки, умноженные на l₂, и т.д., наконец, элементы (r-1)-й строки, умноженные на l_r-1, то r-я строка станет нулевой. При этом по свойствам определителя вышеприведенный определитель не должен измениться, и при этом должен быть равен нулю. Получено противоречие, линейная независимость строк доказана.

Теперь докажем, что любые (r+1) строк матрицы линейно зависимы, т.е. любую строку можно выразить через базисные.

Дополним рассмотренный ранее минор еще одной строкой (i-й) и еще одним столбцом (j-м). В результате получим минор (r+1)-го порядка, который по определению ранга равен нулю:

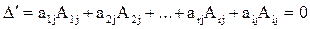
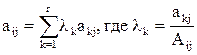
Разложим его по элементам j-го столбца . Здесь последнее алгебраическое дополнение А_ij совпадает с базисным минором D ¹ 0 Þ А_ij ¹ 0. Поэтому можно разделить обе части последнего равенства на А_ij. Это позволит выразить из него элемент: .

Если зафиксировать номер строки (i), то получим, что для любого j элементы i-й строки линейно выражаются через элементы базисных строк: , т.е. любая строка матрицы является линейной комбинацией базисных.

Источник

Матрицы

Определение.

Мы будем называть матрицей размеров \(m \times n\) совокупность \(mn\) чисел, расположенных в виде таблицы из \(m\) строк и \(n\) столбцов:
$$
\begin
a_<1>^<1>& a_<2>^<1>& \ldots & a_^<1>\\
a_<1>^<2>& a_<2>^<2>& \ldots & a_^<2>\\
\ldots&\ldots&\ldots&\ldots\\
a_<1>^& a_<2>^& \ldots& a_^
\end\nonumber
$$
Числа, составляющие матрицу, мы будем называть элементами матрицы. Если число строк в матрице равно числу столбцов, то матрица называется квадратной, а число строк — её порядком. Остальные матрицы носят название прямоугольных.

Можно дать и такое определение матрицы. Рассмотрим два множества целых чисел \(I=<1, 2, \ldots, m>\) и \(J=<1, 2, \ldots, n>\). Через \(I \times J\) обозначим множество всех пар вида \((i, j)\), где \(i \in I\), a \(j \in J\). Матрицей называется числовая функция на \(I \times J\), то есть закон, сопоставляющий каждой паре \((i, j)\) некоторое число \(a_^\).

Для читателя, знакомого с программированием, заметим, что матрица — это в точности то же, что и двумерный массив.

Две матрицы называются равными, если они имеют одинаковые размеры, и равны их элементы, стоящие на одинаковых местах.

Рассматривая произвольные матрицы, мы будем обозначать их элементы буквами с двумя индексами. Если оба индекса расположены внизу, то первый из них обозначает номер строки, а второй — номер столбца; если один из индексов расположен сверху, как в написанной выше матрице, то этот индекс обозначает номер строки. Не следует путать верхние индексы с показателями степени.

Матрицу размеров \(1 \times n\), состоящую из одной строки, мы будем называть строкой длины \(n\) или просто строкой. Матрицу размеров \(m \times 1\) называют столбцом высоты \(m\) или просто столбцом. Столбцы и строки мы будем обозначать полужирными буквами.

Рассмотрим матрицу \(A\) размеров \(m \times n\) и выберем какие-нибудь \(r\) номеров строк \(i_<1>, \ldots, i_\) и \(s\) номеров столбцов \(j_<1>, \ldots, j_\), причем будем предполагать, что номера выбраны в порядке возрастания: \(i_ <1>Определение.

Матрица \(A\) называется симметричной или симметрической, если \(A^=A\). Для такой матрицы \(a_=a_\) при всех \(i\) и \(j\) — элементы, расположенные симметрично относительно главной диагонали, равны.

Матрица \(A\) называется кососимметричной или антисимметричной, если \(A^=-A\). Для такой матрицы \(a_=-a_\) при всех \(i\) и \(j\) — элементы, расположенные симметрично относительно главной диагонали, отличаются знаком. Диагональные элементы равны нулю.

Матрица \(A\) называется верхней треугольной, если ее элементы, расположенные ниже главной диагонали, равны нулю: \(a_=0\) при \(i > j\). Аналогично определяется нижняя треугольная матрица: \(a_=0\) при \(i Определение.

Матрица \(A\) называется диагональной, если у нее равны нулю все недиагональные элементы: \(a_=0\) при \(i \neq j\).

Другие частные виды матриц будем определять по мере необходимости.

Сложение и умножение на число.

Пусть \(A\) и \(B\) — матрицы размеров \(m \times n\). Мы можем сопоставить им третью матрицу \(C\) размеров \(m \times n\), элементы которой \(c_\) связаны с элементами и матриц \(A\) и \(B\) равенствами
$$
c_=a_+b_\ (i=1, \ldots, m,\ j=1, \ldots, n).\label
$$

Матрица \(C\), определяемая по \(A\) и \(B\) формулой \eqref, называется их суммой и обозначается \(A+B\).

Матрица \(C\), элементы которой \(c_\) равны произведениям элементов \(a_\) матрицы \(A\) на число \(\alpha\), называется произведением \(A\) на \(\alpha\) и обозначается \(\alpha A\). Мы имеем
$$
c_=\alpha a_\ (i=1, \ldots, m,\ j=1, \ldots, n).\label
$$

Из свойств сложения и умножения чисел легко вытекает наше первое утверждение.

Для любых матриц \(A, B, C\) и любых чисел \(\alpha\) и \(\beta\) выполнены равенства:

Матрица, все элементы которой равны нулю, называется нулевой матрицей. Если \(O\) — нулевая матрица размеров \(m \times n\), то для любой матрицы тех же размеров
$$
A+O=A.\nonumber
$$

Матрицу \((-1)A\) называют противоположной матрице \(A\) и обозначают \(-A\). Она обладает тем свойством, что
$$
A+(-A)=O.\nonumber
$$

Сумма матриц \(B\) и \(-A\) называется разностью матриц \(B\) и \(A\) и обозначается \(B-A\). Мы видим, что сформулированные выше свойства линейных операций с матрицами совпадают со свойствами линейных операций с векторами. Используя линейные операции, мы можем составлять из матриц одинаковых размеров \(A_<1>, \ldots, A_\) и чисел \(\alpha_<1>, \ldots, \alpha_\), выражения вида
$$
\alpha_<1>A_<1>+\ldots+\alpha_A_.\nonumber
$$

Такие выражения называются линейными комбинациями матриц. Если какая-то матрица представлена как линейная комбинация других матриц, то говорят, что она по ним разложена.

Пусть \(\boldsymbol

_<1>, \ldots, \boldsymbol

_\), — столбцы одинаковой высоты \(n\). Тогда столбец \(\boldsymbol\) той же высоты по ним разложен, если при некоторых коэффициентах \(\alpha_<1>, \ldots, \alpha_\)
$$
\boldsymbol=\alpha_<1>\boldsymbol

_<1>+\ldots+\alpha_\boldsymbol

_,\nonumber
$$
или, в более подробной записи,
$$
\begin q^<1>\\
\vdots\\
q^
\end=\alpha_<1>
\begin p_<1>^<1>\\
\vdots\\
p_<1>^ \end+\ldots+\alpha_ \begin p_^<1>\\
\vdots\\
p_^ \end.\nonumber
$$
В силу определения линейных операций это матричное равенство равносильно \(n\) числовым равенствам
$$
\begin
q^<1>=\alpha_<1>p_<1>^<1>+\ldots+\alpha_p_^<1>,\\
\ldots\\
q^=\alpha_<1>p_<1>^+\ldots+\alpha_p_^.
\end\nonumber
$$

Линейная зависимость матриц.

Какова бы ни была система матриц фиксированных размеров \(m \times n\), нулевая матрица тех же размеров раскладывается по этим матрицам в линейную комбинацию с нулевыми коэффициентами. Такую линейную комбинацию называют тривиальной. Как и для векторов, введем понятие линейной независимости.

Система матриц \(A_<1>, \ldots, A_\) линейно независима, если нулевая матрица раскладывается по ней однозначно, то есть из
$$
\alpha_<1>A_<1>+\ldots+\alpha_A_=O.\label
$$
следует \(\alpha_<1>=\ldots=\alpha_=0\).

В противном случае, то есть если существуют \(k\) чисел \(\alpha_<1>, \ldots, \alpha_\), одновременно не равных нулю и таких, что выполнено равенство \eqref(3), система матриц называется линейно зависимой.

Столбцы
$$
\boldsymbol_<1>=\begin 1\\ 0\\ \vdots\\ 0 \end,\ \boldsymbol_<2>=\begin 0\\ 1\\ \vdots\\ 0 \end,\ \ldots,\ \boldsymbol_=\begin 0\\ 0\\ \vdots\\ 1 \end\label
$$
(в столбце \(\boldsymbol_\) на \(i\)-м месте стоит 1, а остальные элементы равны нулю) являются линейно независимыми. Действительно, равенство \(\alpha_<1>\boldsymbol_<1>+\ldots+\alpha_\boldsymbol_=\boldsymbol<0>\) можно записать подробнее так:
$$
\alpha_ <1>\begin 1\\ 0\\ \vdots\\ 0 \end+\alpha_ <2>\begin 0\\ 1\\ \vdots\\ 0 \end+\ldots+\alpha_ \begin 0\\ 0\\ \vdots\\ 1 \end=\begin \alpha_<1>\\ \alpha_<2>\\ \vdots\\ \alpha_ \end=\begin 0\\ 0\\ \vdots\\ 0 \end.\nonumber
$$
Отсюда видно, что \(\alpha_<1>=\alpha_<2>=\ldots=\alpha_=0\).

Это равенство показывает также, что произвольный столбец высоты \(n\) может быть разложен по столбцам \(\boldsymbol_<1>, \ldots, \boldsymbol_\). Действительно, в качестве коэффициентов линейной комбинации нужно взять элементы раскладываемого столбца.

Квадратная матрица порядка \(n\), состоящая из столбцов \eqref:
$$
E=\begin
1& 0& \ldots& 0\\
0& 1& \ldots& 0\\
\ldots&\ldots&\ldots&\ldots\\
0& 0& \ldots& 1 \end,\nonumber
$$
называется единичной матрицей порядка \(n\) или просто единичной матрицей, если порядок известен.

Строки единичной матрицы отличаются от ее столбцов только формой записи.

Столбцы (строки) единичной матрицы линейно независимы и обладают тем свойством, что каждый столбец (строка) с тем же числом элементов раскладывается по ним.

Укажем несколько свойств линейно зависимых и линейно независимых систем матриц.

Система из \(k > 1\) матриц линейно зависима тогда и только тогда, когда хотя бы одна из матриц есть линейная комбинация остальных.

В самом деле, пусть система линейно зависима. По определению выполнено равенство вида \eqref, где хотя бы один коэффициент отличен от нуля. Допустим для определенности, что это \(\alpha_<1>\). Тогда мы можем представить первую матрицу как линейную комбинацию
$$
A_<1>=-\frac<\alpha_<2>><\alpha_<1>>A_<2>-\ldots-\frac<\alpha_><\alpha_<1>>A_.
$$
Обратно, если одна из матриц разложена по остальным, то это разложение преобразуется к виду \eqref, где один из коэффициентов равен 1.

Если некоторые из матриц \(A_<1>, \ldots, A_\) составляют сами по себе линейно зависимую систему, то вся система \(A_<1>, \ldots, A_\) линейно зависима.

Действительно, пусть существует нетривиальная линейная комбинация некоторых из матриц системы, равная нулевой матрице. Если мы добавим к ней остальные матрицы с нулевыми коэффициентами, то получится равная нулевой матрице нетривиальная линейная комбинация всех матриц.

В частности, если в систему матриц входит нулевая матрица, то система линейно зависима.

Любые матрицы, входящие в линейно независимую систему матриц, сами по себе линейно независимы.

В самом деле, в противном случае мы пришли бы к противоречию на основании предыдущего утверждения.

Если матрица \(B\) разложена по линейно независимой системе матриц \(A_<1>, \ldots, A_\), то коэффициенты разложения определены однозначно.

Действительно, пусть мы имеем два разложения
$$
B=\alpha_<1>A_<1>+\ldots+\alpha_A_\ \mbox<и>\ B=\beta_<1>A_<1>+\ldots+\beta_A_.\nonumber
$$
Вычитая одно разложение из другого, мы получаем
$$
O=(\alpha_<1>-\beta_<1>)A_<1>+\ldots+(\alpha_-\beta_)A_.\nonumber
$$
Матрицы \(A_<1>, \ldots, A_\) линейно независимы, значит, \(\alpha_-\beta_=0\) для всех \(i=1, \ldots, k\). Итак, коэффициенты обоих разложений совпадают.

Источник

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

kdnuggets

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:

Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

TimoElliott

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

Ортогональные матрицы

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

TimoElliott

Область значений и нуль-пространство матрицы

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают

Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx

), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

Собственные значения и собственные векторы

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

Источник