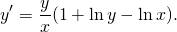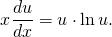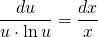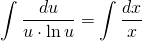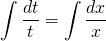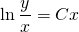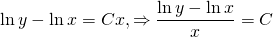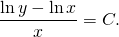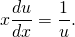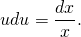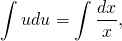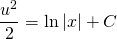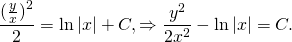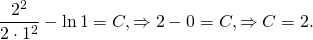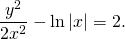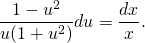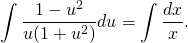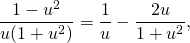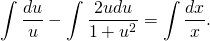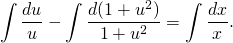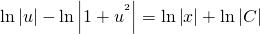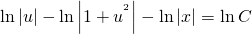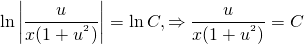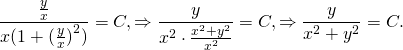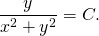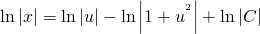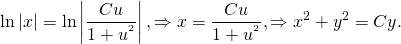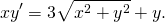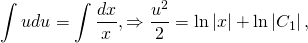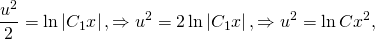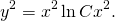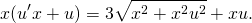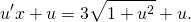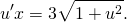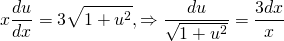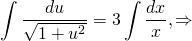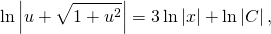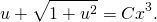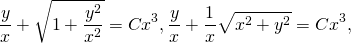Как доказать что уравнение однородное

16.10.202311.06.2023 admin 0 Comments

Как доказать что уравнение однородное

Однородное дифференциальное уравнение можно решить с помощью подстановки \(y = ux,\) которая преобразует однородное уравнение в уравнение с разделяющимися переменными.

Дифференциальное уравнение вида \[\left( <x + y + > \right)dx + \left( <x + y + > \right)dy = 0\] преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной: \[z = ax + by.\]

Нетрудно заметить, что многочлены \(P\left( \right)\) и \(Q\left( \right),\) соответственно, при \(dx\) и \(dy,\) являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным.

Интегрируем последнее выражение: \[\int = 2\int <\frac<>> \;\;\text<или>\;\;u = 2\ln \left| x \right| + C,\] где \(C\) − постоянная интегрирования.

Возвращаясь к старой переменной \(y,\) можно записать: \[y = ux = x\left( <2\ln \left| x \right| + C>\right).\] Таким образом, уравнение имеет два решения: \[y = x\left( <2\ln \left| x \right| + C>\right),\;\;x = 0.\]

Заметим, что корень \(x = 0\) не принадлежит области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме: \[y’ = \frac\ln \frac = f\left( <\frac> \right).\] Как видно, уравнение является однородным.

Здесь мы снова встречаемся с однородным уравнением. В самом деле, запишем его в виде: \[ >><>> > = <\frac<<\frac<<>><<>>>><<\frac<><<>> + \frac<<>><<>>>> > = <\frac<<<<\left( <\frac> \right)>^2>>><<\frac + <<\left( <\frac> \right)>^2>>> > = > \right).> \] Сделаем подстановку \(y = ux.\) Тогда \(y’ = u’x + u.\) Подставляя \(y\) и \(y’\) в исходное уравнение, получаем: \[ <\left( > \right)\left( \right) = ,>\;\; <\Rightarrow u\left( \right)\left( \right) = .> \] Разделим обе части уравнения на \(u.\) Заметим, что корень \(x = 0\) не является решением, но можно убедиться, что корень \(u = 0\) (или \(y = 0\)) будет одним из решений данного дифференциального уравнения.

Источник

Как решить однородное дифференциальное уравнение

Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения: y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.

Примеры решения однородных дифференциальных уравнений 1-го порядка.

1) Решить уравнение

Проверяем, что это уравнение является однородным (см. Как определить однородное уравнение). Убедившись, делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем: u’x+u=u(1+ln(ux)-lnx). Так как логарифм произведения равен сумме логарифмов, ln(ux)=lnu+lnx. Отсюда

u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки

u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,

Получили уравнение с разделяющимися переменными. Разделяем переменные, для чего обе части умножаем на dx и делим на x·u·lnu, при условии, что произведение x·u·lnu≠0

В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u

ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда

ln│t│=ln│x│+ln│C│. По свойству логарифмов: ln│t│=ln│Сx│. Отсюда t=Cx. ( по условию, x>0). Пора делать обратную замену: lnu=Cx. И еще одна обратная замена:

По свойству логарифмов:

Это — общий интеграл уравнения.

Вспоминаем условие произведение x·u·lnu≠0 (а значит, x≠0,u≠0, lnu≠0, откуда u≠1). Но x≠0 из условия, остается u≠1, откуда x≠y. Очевидно, что y=x ( x>0) входят в общее решение.

2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.

Сначала проверяем, что это уравнение является однородным (хотя наличие слагаемых y/x и x/y уже косвенно указывает на это). Затем делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем полученные выражения в уравнение:

u’x=1/u. Так как u — функция от икса, u’=du/dx:

Получили уравнение с разделяющимися переменными. Чтобы разделить переменные, умножаем обе части на dx и u и делим на x (x≠0 по условию, отсюда u≠0 тоже, значит, потери решений при этом не происходит).

и поскольку в обеих частях стоят табличные интегралы, сразу же получаем

Выполняем обратную замену:

Это — общий интеграл уравнения. Используем начальное условие y(1)=2, то есть подставляем в полученное решение y=2, x=1:

3) Найти общий интеграл однородного уравнения:

(x²-y²)dy-2xydx=0.

Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:

(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):

(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:

xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:

(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:

x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:

x(1-u²)du=u(u²+1)dx. Для этого обе части уравнения делим на xu(u²+1)≠0 (соответственно, добавляем требования x≠0 (уже отметили), u≠0):

В правой части уравнения — табличный интеграл, рациональную дробь в левой части раскладываем на простые множители:

(или во втором интеграле можно было вместо подведения под знак дифференциала сделать замену t=1+u², dt=2udu — кому какой способ больше нравится). Получаем: