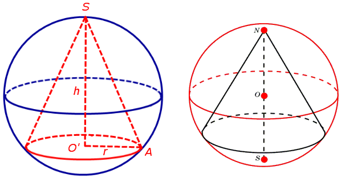
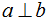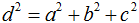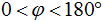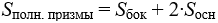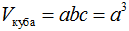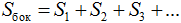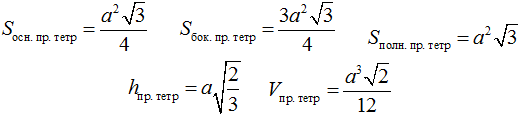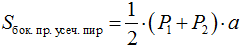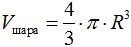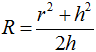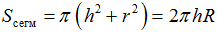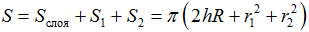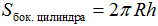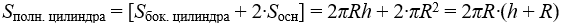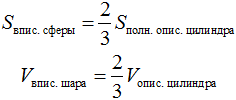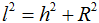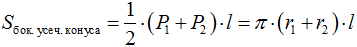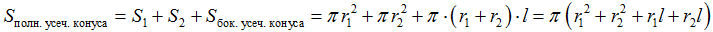Как доказать что в правильном тетраэдре скрещивающиеся ребра перпендикулярны
Теорема о трех перпендикулярах
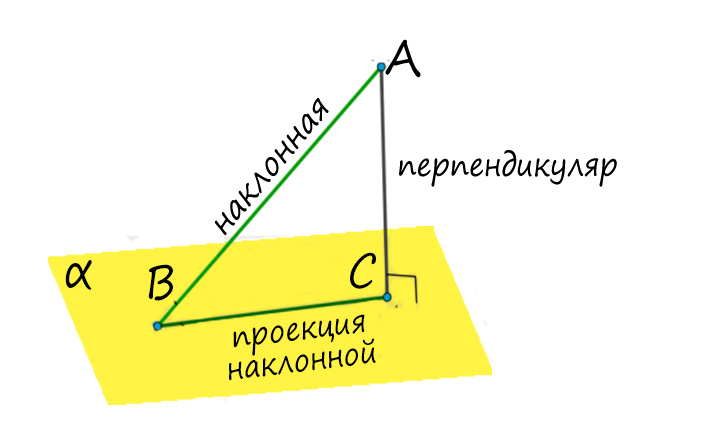
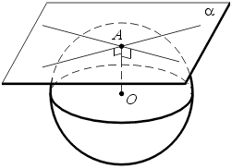
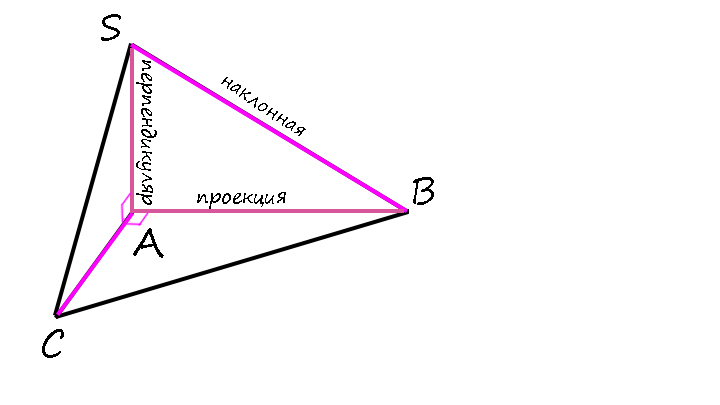
Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а1 — проекция наклонной а на плоскость α.
Сформулируем теорему о трех перпендикулярах:
Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.
На рисунке показаны все три перпендикуляра.
Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.
Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.
Ты нашел то, что искал? Поделись с друзьями!
Вот как все это выглядит в пространстве:
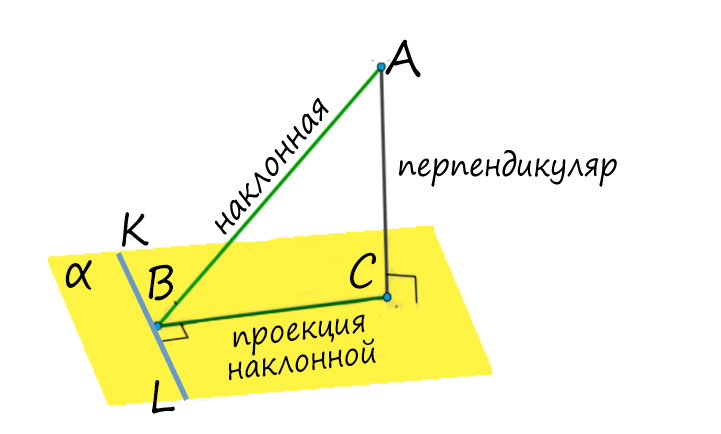
На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:
Теорема о трех перпендикулярах — полезный инструмент для решения задач.
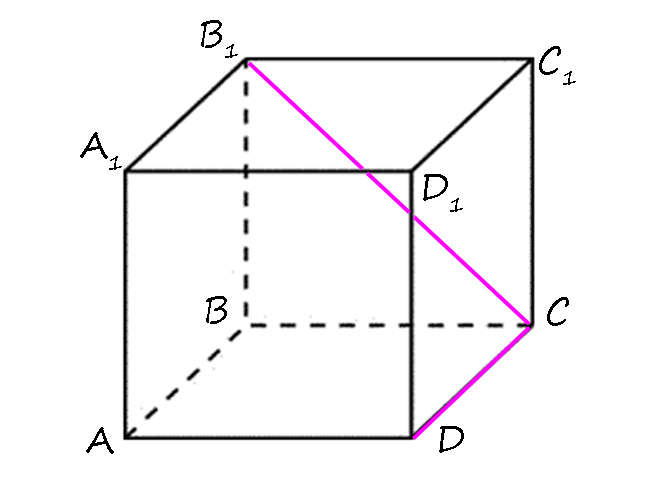
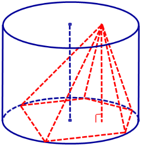
Например, с ее помощью можно доказать, что диагональ куба АС1 перпендикулярна прямой BD:
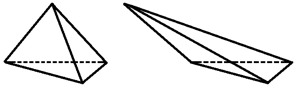
Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:
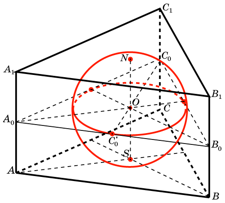
Или — что в правильной треугольной призме прямая А1М (где М — середина ВС) перпендикулярна ребру ВС.
Теорема о трех перпендикулярах
Как ее использовать в задачах
Как оформлять на ЕГЭ
Начнем с парочки вводных понятий, ты же хочешь жить по понятиям?
Если в плоскости альфа провести прямую KL через точку В так, что KL ⊥ BC, тогда по теореме о трех перпендикулярах (т.т.п.) KL ⊥ BA.
Словами можно сказать так: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость (верно и наоборот).
Перейдем к самому распространенному примеру:
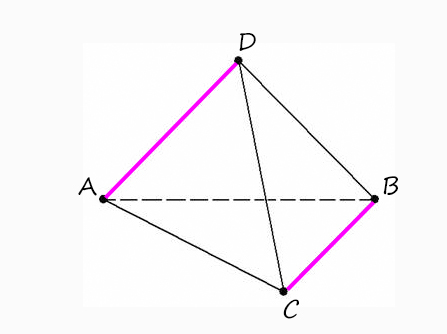
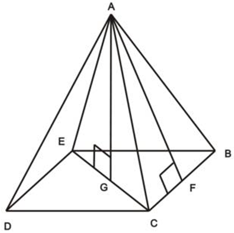
1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны.
У тетраэдра есть три пары скрещивающихся ребер. Докажем перпендикулярность одной пары, другие вы сделаете по аналогии, например, AD ⊥ BC.
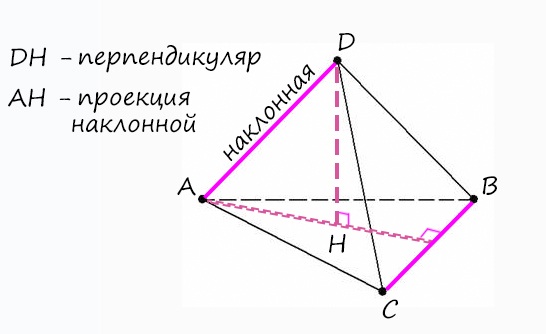
Сейчас есть только наклонная AD и плоскость (ABC), значит, нам не хватает проекции наклонной и перпендикуляра, тогда проведем их:
Тогда, чтобы доказать, что AD ⊥ BC:
1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике.
2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) => DH ⊥ BC.
После того, как мы это доказали, можем смело сказать, что AD ⊥ BC (всегда дожно быть доказательство двух пунктов, и только тогда вывод).
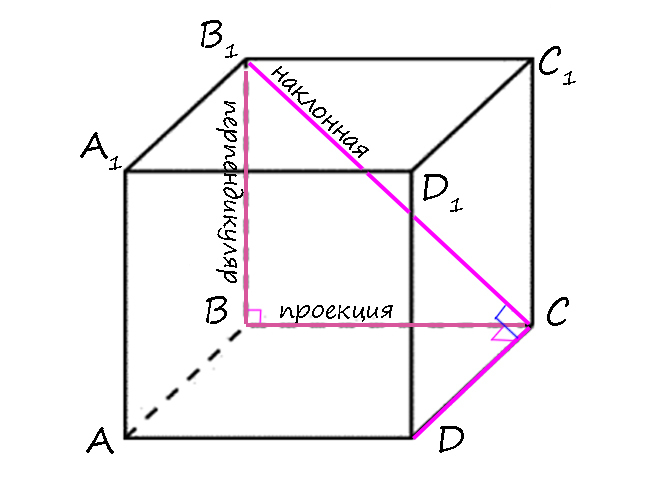
2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.
Возьмем B₁C как наклонную к плоскости (ABCD), тогда перпендикуляром будет BB₁, а проекцией наклонной на эту плоскость — BC.
1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) => BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то и перпендикулярна всем прямым, лежащим в этой плоскости).
2) BC ⊥ CD т.к. ABCD — прямоугольник.
3) По т.т.п.: B₁C ⊥ CD.
Два пункта доказательства, третий пункт вывод.
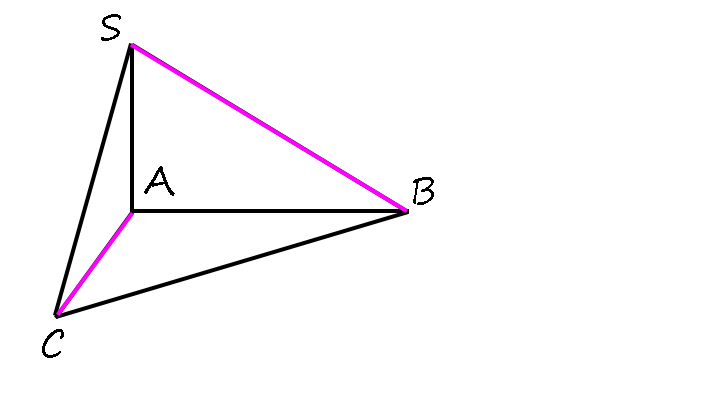
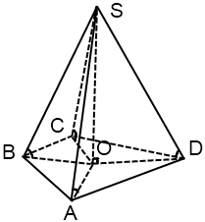
3) Дана пирамида SABC с высотой AS, в основании которой лежит прямоугольный треугольник с прямым углом A. Докажите, что SB⊥ AC.
Скажем, что BC — наклонная к плоскости (ABC):
1) SA ⊥ (ABC) => SA ⊥ AC
2) AB ⊥ AC ( ABC — прямоугольный треугольник по условию).
Два пункта доказательство и вывод!
1) Перпендикуляр будет опускаться на плоскость под 90 °.
2) Проекция наклонной на плоскость перпендикулярна прямой.
3) По т.т.п. наклонная перпендикулярна прямой.
Избранные теоремы геометрии тетраэдра (стр. 6 из 9)
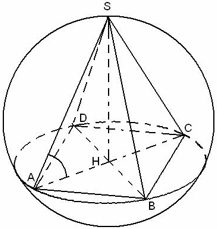
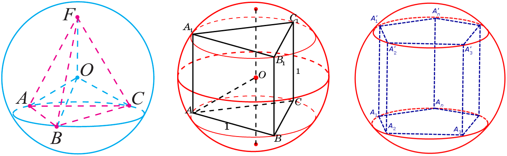
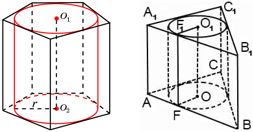
Доказать, что скрещивающиеся ребра правильного тетраэдра взаимно перпендикулярны.
Пусть DH – высота правильного тетраэдра, точка H – центр правильного ΔABC. Тогда проекцией отрезка AD на плоскость основания ABC будет отрезок BH. Т.к. BH AC, то по теореме о трех перпендикулярах наклонная BD AC.
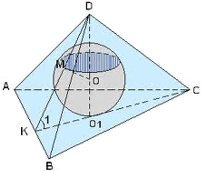
Дан правильный тетраэдр МАВС с ребром 1. найдите расстояние между прямыми AL и МО, где L-середина ребра МС, О-центр грани АВС.
Каждое ребро треугольной пирамиды PABCравно 1; BD– высота треугольника ABC. Равносторонний треугольник BDEлежит в плоскости, образующей угол ϕс ребром AC, причём точки Pи Eлежат по одну сторону от плоскости ABC. Найдите расстояние между точками Pи E.
Решение. Поскольку все рёбра пирамиды PABCравны, это правильный тетраэдр. Пусть M – центр основания ABC, N– ортогональная проекция вершины Eравностороннего треугольника BDEна плоскость ABC,K– середина BD,F– основание перпендикуляра, опущенного из точки Eна высоту PMтетраэдра PABC. Так какEK
Найди углы между скрещивающимися высотами соседних граней тетраэдра.
Пусть BK и DF – высоты граней ABC и BCD.
Запишем теорему косинусов для ΔDLF:
Случай №2 (высота расположена иначе).
BK и CN – высоты граней ABC и BCD. Проведем FP || CN и FL || BK.
Запишем теорему косинусов для ΔLFP:
Так как угол между прямыми по определению острый
Глава II. Тетраэдр в курсе математики средней школы
§1. Сравнительная характеристика изложения темы «тетраэдр» в школьных учебниках
Однако проблемы в изучении темы для учащихся существуют, и разные учебники пытаются решить их разными способами (порядком изложения теоретического материала, уровнем сложности задач и т.п.). Дадим краткую характеристику распространенных учебников геометрии в аспекте изучения тетраэдра.
Изложение темы «Тетраэдр» в учебнике «Геометрия» для 10-11 классов Атанасяна Л. С. и др.
В базовом учебнике «Геометрия» для 10-11 классов средней школы Атанасяна Л. С. и др. информацию о тетраэдре можно найти в 7 параграфах (12, 14, 28, 29, 32, 33, 69).
Как доказать что в правильном тетраэдре скрещивающиеся ребра перпендикулярны
Некоторые определения:
Аксиомы стереометрии:
Следствия из аксиом стереометрии:
Построение сечений в стереометрии
Для решения задач по стереометрии остро необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Дадим несколько определений, поясняющих, что такое сечение:
Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна. В основе построения сечений многогранников лежит две задачи на построение:
Для построения прямой, по которой пересекаются некоторые две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β.
Взаимное расположение прямых и плоскостей в стереометрии
Определение: В ходе решения задач по стереометрии две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Если прямые а и b, либо AB и CDпараллельны, то пишут:
Несколько теорем:
Возможны три случая взаимного расположения прямой и плоскости в стереометрии:
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямаяа параллельна плоскости β, то пишут:
Теоремы:
Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).
Определение: Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.
Теоремы:
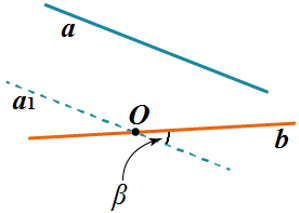
Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Это обычно не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между скрещивающимися прямыми дадим такое определение:
Определение: Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a 1 параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a 1 и b).
Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90°. Перпендикулярными могут быть как скрещивающиеся прямые, так и прямые лежащие и пересекающиеся в одной плоскости. Если прямая a перпендикулярна прямой b, то пишут:
Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:
Теоремы:
Определение: Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если прямая a перпендикулярна плоскости β, то пишут, как обычно:
Теоремы:
Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.
Теорема о трех перпендикулярах
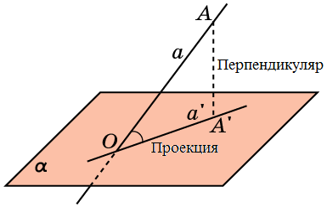
Пусть точка А не лежит на плоскости α. Проведем через точку А прямую, перпендикулярную плоскости α, и обозначим буквой О точку пересечения этой прямой с плоскостью α. Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АО, точка О называется основанием перпендикуляра. Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.
Теорема 1 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:
Теорема 2 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость. Данные теоремы, для обозначений с чертежа выше можно кратко сформулировать так:
Теорема: Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:
Определения расстояний объектами в пространстве:
Определение: В стереометрии ортогональной проекцией прямой a на плоскость α называется проекция этой прямой на плоскость α в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости α.
Замечание: Как видно из предыдущего определения, проекций бывает много. Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).
Определение: Углом между прямой, не перпендикулярной плоскости, и этой плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость (угол АОА’ на чертеже выше).
Теорема: Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.
Двугранный угол
Определения:
Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). В дальнейшем, при решении задач по стереометрии, под двугранным углом будем понимать всегда тот линейный угол, градусная мера которого удовлетворяет условию:
Определения:
Теоремы:
Симметрия фигур
Определения:
Призма
Определения:
Свойства и формулы для призмы:
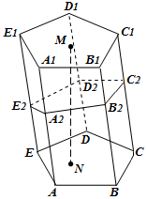
где: S осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
где: S сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA 1 или BB 1 и так далее).
где: P сеч – периметр перпендикулярного сечения, l – длина бокового ребра.
Виды призм в стереометрии:
где: P осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S осн ∙h = S осн ∙l.
Свойства правильной призмы:
Параллелепипед
Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.
Другие свойства и определения:
Пирамида
Определения:
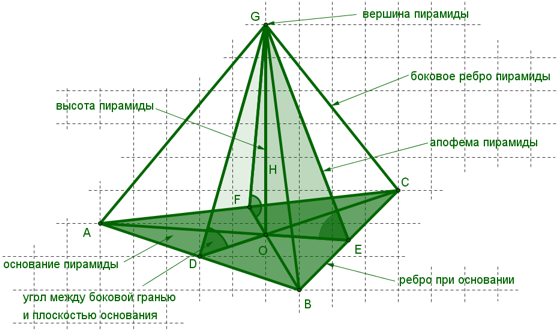
Еще один стереометрический чертеж с обозначениями для лучшего запоминания (на рисунке правильная треугольная пирамида):
Если все боковые ребра (SA, SB, SC, SD на чертеже ниже) пирамиды равны, то:
Важно: Также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом (углы DMN, DKN, DLN на чертеже ниже равны), то:
где: P – периметр основания, a – длина апофемы.
Важно: Также верно и обратное, то есть если в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в её центр, то все боковые грани наклонены к плоскости основания под одним углом и высоты боковых граней (апофемы) равны.
Правильная пирамида
Определение: Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
Важное замечание: Как видим правильные пирамиды являются одними из тех пирамид к которым относятся свойства, изложенные чуть выше. Действительно, если основание правильной пирамиды – это правильный многоугольник, то центр его вписанной и описанной окружностей совпадают, а вершина правильной пирамиды проецируется именно в этот центр (по определению). Однако важно понимать, что не только правильныепирамиды могут обладать свойствами, о которых говорилось выше.
Формулы для объема и площади пирамиды
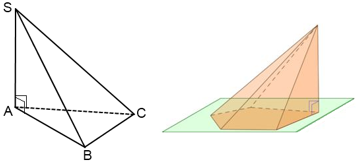
Теорема (об объеме пирамид, имеющих равные высоты и равные площади оснований). Две пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы (Вы конечно, наверняка уже знаете формулу для объема пирамиды, ну или видите ее несколькими строчками ниже, и Вам кажется это утверждение очевидным, но на самом деле, если судить «на глаз», то данная теорема не так уж и очевидна (см. рисунок ниже). Это относится кстати и к другим многогранникам и геометрическим фигурам: их внешний вид обманчив, поэтому, действительно – в математике нужно доверять только формулам и правильным расчетам).
где: S осн – площадь основания пирамиды, h – высота пирамиды.
Тетраэдр
Определения:
На чертеже изображен правильный тетраэдр, при этом треугольники ABC, ADC, CBD, BAD – равны. Из общих формул для объема и площадей пирамиды, а также знаний из планиметрии не сложно получить формулы дляобъема и площадей правильного тетраэдра (а – длина ребра):
Прямоугольная пирамида
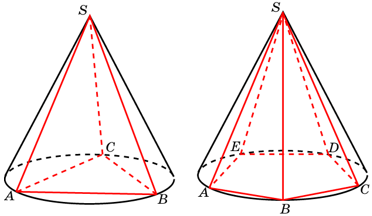
Определение: При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид. На рисунке слева SA – ребро, являющееся одновременно высотой.
Усечённая пирамида
Определения и свойства:
Формулы для усеченной пирамиды
Объём усечённой пирамиды равен:
где: S 1 и S 2 – площади оснований, h – высота усечённой пирамиды. Однако на практике, удобнее искать объем усеченной пирамиды так: можно достроить усечённую пирамиду до пирамиды, продлив до пересечения боковые рёбра. Тогда объём усечённой пирамиды можно найти, как разность объёмов всей пирамиды и достроенной части. Площадь боковой поверхности также можно искать как разность между площадями боковой поверхности всей пирамиды и достроенной части. Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы:
где: P 1 и P 2 – периметры оснований правильной усеченной пирамиды, а – длина апофемы. Площадь полной поверхности любой усеченной пирамиды, очевидно, находится как сумма площадей оснований и боковой поверхности:
Пирамида и шар (сфера)
Теорема: Около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (т.е. многоугольник около которого можно описать сферу). Данное условие является необходимым и достаточным. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им.
Замечание: Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу. Однако, список пирамид около которых можно описать сферу не исчерпывается этими типами пирамид. На чертеже справа, на высоте SH надо выбрать точку О, равноудалённую от всех вершин пирамиды: SO = OВ = OС = OD = OA. Тогда точка О – центр описанного шара.
Теорема: В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Замечание: Вы, очевидно, не поняли того, что прочитали строчкой выше. Однако, главное запомнить, что любая правильная пирамида является такой, в которую можно вписать сферу. При этом список пирамид, в которые можно вписать сферу не исчерпывается правильными.
Определение: Биссекторная плоскость делит двугранный угол пополам, а каждая точка биссекторной плоскости равноудалена от граней, образующих двугранный угол. На рисунке справа плоскость γ является биссекторной плоскостью двугранного угла, образованного плоскостями α и β.
На стереометрическом чертеже ниже изображен шар вписанный в пирамиду (или пирамида описанная около шара), при этом точка О – центр вписанного шара. Данная точка О равноудалена от всех граней шара, например:
Пирамида и конус
В стереометрии конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие).
Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие).
Важное свойство: Высоты у таких конусов и пирамид равны между собой.
Пирамида и цилиндр
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды – вписанный многоугольник (необходимое и достаточное условие).
Сфера и шар
Определения:
Теоремы:
Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. Aи B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
Определения:
Теоремы:
Многогранники и сфера
Определение: В стереометрии многогранник (например, пирамида или призма) называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника (пирамиды, призмы). Аналогично: многогранник называется вписанным в шар, если все его вершины лежат на границе этого шара. При этом шар называется описанным около многогранника.
Важное свойство: Центр сферы, описанной около многогранника, находится на расстоянии, равном радиусу R сферы, от каждой вершины многогранника. Приведем примеры вписанных в сферу многогранников:
Определение: Многогранник называется описанным около сферы (шара), если сфера (шар) касается всехграней многогранника. При этом сфера и шар называются вписанными в многогранник.
Важно: Центр сферы, вписанной в многогранник, находится на расстоянии, равном радиусу r сферы, от каждой из плоскостей, содержащих грани многогранника. Приведем примеры описанных около сферы многогранников:
Объем и площадь поверхности шара
Теоремы:
где: R – радиус сферы.
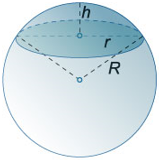
Шаровой сегмент, слой, сектор
Шаровой сегмент
В стереометрии шаровым сегментом называется часть шара, отсекаемая секущей плоскостью. При этом соотношение между высотой, радиусом основания сегмента и радиусом шара:
где: h − высота сегмента, r − радиус основания сегмента, R − радиус шара. Площадь основания шарового сегмента:
Площадь внешней поверхности шарового сегмента:
Площадь полной поверхности шарового сегмента:
Объем шарового сегмента:
Шаровой слой
В стереометрии шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями. Площадь внешней поверхности шарового слоя:
где: h − высота шарового слоя, R − радиус шара. Площадь полной поверхности шарового слоя:
Шаровой сектор
В стереометрии шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше чем пол шара. Площадь полной поверхности шарового сектора:
где: h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара. Объем шарового сектора вычисляется по формуле:
Цилиндр
Определения:
Цилиндр и призма
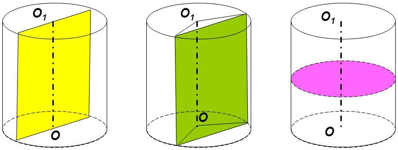
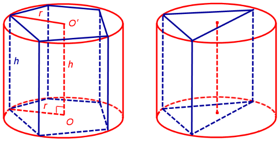
Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра. В этом случае цилиндр называется описанным около призмы. Высота призмы и высота цилиндра в этом случае будут равны. Все боковые ребра призмы будут принадлежать боковой поверхности цилиндра и совпадать с его образующими. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать в такой цилиндр можно также только прямую призму. Примеры:
Призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра. В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые ребра призмы будут параллельны образующим цилиндра. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать такой цилиндр можно только в прямую призму. Примеры:
Цилиндр и сфера
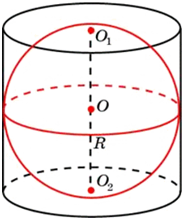
Сфера (шар) называется вписанной в цилиндр, если она касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным около сферы (шара). Сферу можно вписать в цилиндр, только если это равносторонний цилиндр, т.е. диаметр его основания и высота равны между собой. Центром вписанной сферы будет служить середина оси цилиндра, а радиус этой сферы будет совпадать с радиусом цилиндра. Пример:
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра являются сечениями сферы. Цилиндр называется вписанным в шар, если основания цилиндра являются сечениями шара. При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:
На основе теоремы Пифагора легко доказать следующую формулу, связывающую радиус описанной сферы (R), высоту цилиндра (h) и радиус цилиндра (r):
Объем и площадь боковой и полной поверхностей цилиндра
Теорема 1 (о площади боковой поверхности цилиндра): Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту:
где: R – радиус основания цилиндра, h – его высота. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности прямой призмы.
Площадью полной поверхности цилиндра, как обычно в стереометрии, называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра (т.е. просто площадь круга) вычисляется по формуле:
Следовательно, площадь полной поверхности цилиндра S полн. цилиндра вычисляется по формуле:
Теорема 2 (об объеме цилиндра): Объем цилиндра равен произведению площади основания на высоту:
где: R и h – радиус и высота цилиндра соответственно. Эта формула также легко выводится (доказывается) на основе формулы для объема призмы.
Теорема 3 (Архимеда): Объём шара в полтора раза меньше объёма, описанного вокруг него цилиндра, а площадь поверхности такого шара в полтора раза меньше площади полной поверхности того же цилиндра:
Конус
Определения:
Объем и площадь боковой и полной поверхностей конуса
Теорема 1 (о площади боковой поверхности конуса). Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
где: R – радиус основания конуса, l – длина образующей конуса. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности правильной пирамиды.
Теорема 2 (об объеме конуса). Объем конуса равен одной трети произведения площади основания на высоту:
где: R – радиус основания конуса, h – его высота. Эта формула также легко выводится (доказывается) на основе формулы для объема пирамиды.
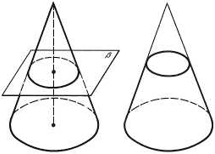
Усеченный конус
Определения:
Формулы для усеченного конуса:
Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Объём усечённого конуса вычисляется по формуле:
где: S 1 = πr 1 2 и S 2 = πr 2 2 – площади оснований, h – высота усечённого конуса, r 1 и r 2 – радиусы верхнего и нижнего оснований усеченного конуса. Однако на практике, всё же удобнее искать объем усеченного конуса как разность объёмов исходного конуса и отсеченной части. Площадь боковой поверхности усеченного конуса также можно искать как разность между площадями боковой поверхности исходного конуса и отсеченной части.
Действительно, площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса вычисляется по формуле:
где: P 1 = 2πr 1 и P 2 = 2πr 2 – периметры оснований усеченного конуса, l – длина образующей. Площадь полной поверхности усеченного конуса, очевидно, находится как сумма площадей оснований и боковой поверхности:
Обратите внимание, что формулы для объема и площади боковой поверхности усеченного конуса получены на основе формул для аналогичных характеристик правильной усеченной пирамиды.
Конус и сфера
Конус называется вписанным в сферу (шар), если его вершина принадлежит сфере (границе шара), а окружность основания (само основание) является сечением сферы (шара). При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:
Сфера (шар) называется вписанной в конус, если сфера (шар) касается основания конуса и каждой его образующей. При этом конус называется описанным около сферы (шара). В прямой круговой конус всегда можно вписать сферу. Её центр будет лежать на высоте конуса, а радиус вписанной сферы будет равен радиусу окружности, вписанной в осевое сечение конуса (это сечение является равнобедренным треугольником). Примеры: