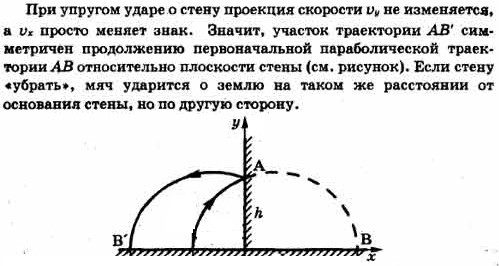
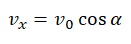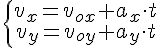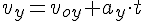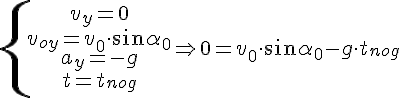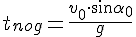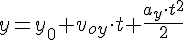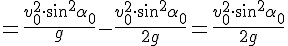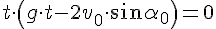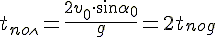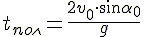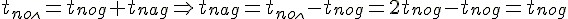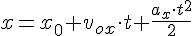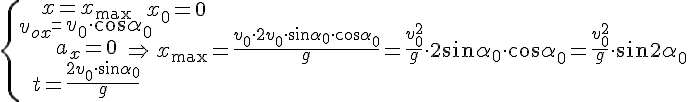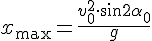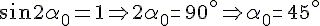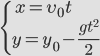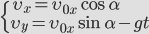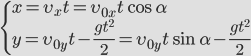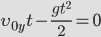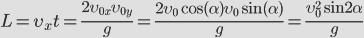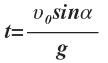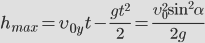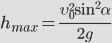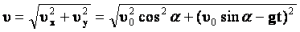Как доказать что время подъема равно времени падения
Движение тела, брошенного под углом к горизонту
теория по физике 🧲 кинематика
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты! График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
Уравнение координаты x:
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Потенциальная энергия шарика в точке А равна:
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
Перед ударом кинетическая энергия шарика равна:
Согласно закону сохранения энергии:
E p A = E p B + E k B
Отсюда высота H равна:
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
pазбирался: Алиса Никитина | обсудить разбор | оценить
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Как доказать что время подъема равно времени падения
§ 35. Движение тела, брошенного под углом к горизонту
1. Постоянство ускорения.
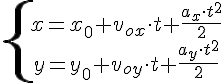
2. Нахождение времени подъёма до наивысшей точки и максимальной высоты подъёма.
Это время легко найти из формулы проекции скорости на ось OY, т.к. в наивысшей точке подъёма скорость направлена горизонтально, т.е. перпендикулярно оси OY, и её проекция на эту ось равна нулю.
Максимальную высоту подъёма найдём из уравнения координаты по оси OY.
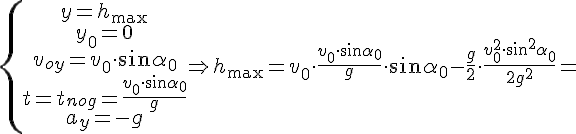
3. Время полёта и время падения.
Время полёта находится из уравнения координаты y.
Если выбрать ось OX так, чтобы она проходила через точку падения, то в конце полёта тело упадёт на ось OX, где y=0. Если точка бросания и точка падения находятся на одном уровне, то время подъёма равно времени падения, а время полёта будет в 2 раза больше.
Действительно:
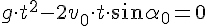
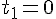
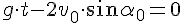
Если точки бросания и падения не лежат на одном уровне, то эти соотношения не выполняются, но находить их также.
4. Дальность полёта, когда точки бросания и падения находятся на одном уровне.
Для нахождения дальности полёта в уравнение координаты x надо подставить время полёта.
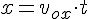
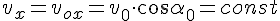
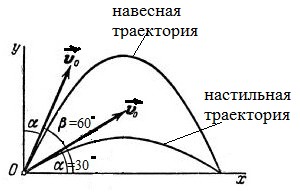
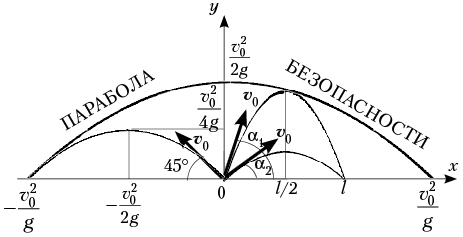
4а. Найдём угол, при котором дальность полёта при заданной начальной скорости будет наибольшей.
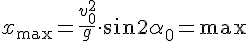
4б. Покажем, что дальность полёта тел, брошенных под углами 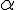
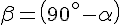
Действительно, если 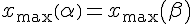
Таким образом, дальность полёта тел, брошенных по настильной траектории (под углом 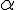
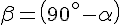
В частности, это выполняется для углов 30 градусов и 60 градусов (см. рис. выше).
7. Баллистическая траектория.
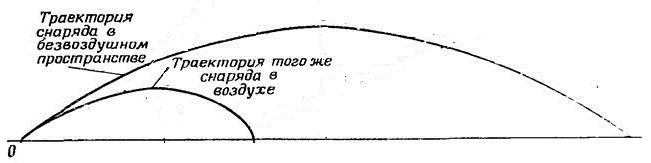
Изложенные выше формулы и рассуждения справедливы в том случае, если мы не учитываем сопротивление воздуха. В реальных ситуациях тела движутся по так называемым баллистическим кривым, или баллистическим траекториям, которые отличаются от правильной параболической формы.
Баллистическая траектория — это траектория, по которой движется тело, обладающее некоторой начальной скоростью, под действием силы тяготения и силы аэродинамического сопротивления воздуха.
Форма участков баллистической траектории, проходящих в плотных слоях атмосферы зависит от многих факторов: начальной скорости тела, его формы и массы, текущего состояния атмосферы на траектории (температура, давление, плотность), направления вращения Земли и от характера движения тела вокруг его центра масс. Форма баллистической траектории в этом случае обычно рассчитывается методом численного интегрирования дифференциальных уравнений движения тела в стандартной атмосфере (условном вертикальном распределении температуры, давления и плотности воздуха в атмосфере Земли, принятом международной организацией по стандартизации).
1) В точке наивысшего подъёма 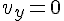
3) Если точки бросания и падения находятся на одном уровне, то
4) Если точки бросания и падения находятся на одном уровне, то направляющие косинусы в точке бросания и точке падения одинаковы 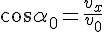
5) На одной и той же высоте (по вертикали) от точки бросания скорости подъёма и падения одинаковы, а также равны направляющие косинусы этих скоростей.
6) Наибольшая дальность полёта при заданной начальной скорости будет при угле бросания 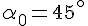
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Движение тела, брошенного горизонтально или под углом к горизонту.
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
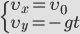
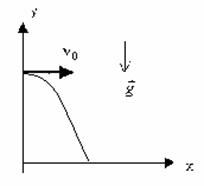
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
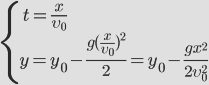
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
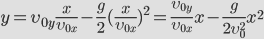
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ;
— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
Ускорение свободного падения
Тестирование онлайн
Свободное падение. Ускорение
Свободным падение будем называть движение предметов вертикально вниз или вертикально вверх. Это равноускоренное движение, но особый его вид. Для этого движения справедливы все формулы и законы равноускоренного движения.
Если тело летит вертикально вниз, то оно ускоряется, в этом случае вектор скорости (направлен вертикально вниз) совпадает с вектором ускорения. Если тело летит вертикально вверх, то оно замедляется, в этом случае вектор скорости (направлен вверх) не совпадает с направлением ускорения. Вектор ускорения при свободном падении всегда направлен вертикально вниз.
Ускорение при свободном падении тел является постоянной величиной.
Это означает какое бы тело не летело вверх или вниз, его скорость будет изменяться одинаково. НО с одной оговоркой, еслисилой сопротивления воздуха можно пренебречь.
Ускорение свободного падения принято обозначать буквой, отличной от ускорения. Но ускорение свободного падения иускорение это одна и та же физическая величина и имеют они одинаковый физический смысл. Участвуют одинаково в формулах для равноускоренного движения.
Почему тела в вакууме падают одинаково?
Всем известно из школьных учебников физики, что в вакууме камушек и перышко летят одинаково. Но мало кто понимает, почему же в вакууме тела разной массы приземляются одновременно. Как ни крути, будь они в вакууме или в воздухе масса у них разная. Ответ прост. Сила, которая заставляет тела падать (сила тяжести), вызываемая гравитационным полем Земли у этих тел разная. У камня она больше (так как у камня больше масса), у перышка она меньше. Но здесь нет зависимости: чем больше сила, тем больше ускорение! Сравним, действуем с одинаковой силой на тяжелый шкаф и легкую тумбочку. Под действием этой силы тумбочка будет перемещаться быстрее. А для того, чтобы шкаф и тумбочка двигались одинаково, на шкаф необходимо воздействовать сильнее, чем на тумбочку. То же самое проделывает Земля. Более тяжелые тела она притягивает с большей силой, чем легкие. И эти силы так распределяются между массами, что все они в результате падают в вакууме одновременно, независимо от массы.
Отдельно рассмотрим вопрос о возникающем сопротивлении воздуха. Возьмем два одинаковых листа бумаги. Один из них скомкаем и одновременно отпустим из рук. Скомканный лист упадет на землю раньше. Здесь разное время падения не связано с массой тела и силой тяжести, а обусловлено сопротивлением воздуха.
Падение тела с некоторой высоты
Рассмотрим падение тела с некоторой высоты h без начальной скорости. Если координатную ось ОУ направить вверх, совместив начало координат с поверхностью Земли, получим основные характеристики этого движения.
Свободное падение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равноускоренно с ускорением свободного падения. В этом случае векторы скорости и ускорения направлены в противоположные стороны, а модуль скорости с течением времени уменьшается.

Главное запомнить
1) Направление ускорения при свободном падении тела;
2) Численное значение ускорения свободного падения;
3) Формулы
Вывести формулу для определения времени падения тела с некоторой высотыh без начальной скорости.
Вывести формулу для определения времени подъема тела до максимальной высоты, брошенного с начальной скоростью v0
Вывести формулу для определения максимальной высоты подъема тела, брошенного вертикально вверх с начальной скоростью v0