Как показать что точка принадлежит прямой

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Проверка принадлежности точки прямой

Проверка принадлежности точки прямой (Паскаль)

Пример. Составить программу для определения лежит ли точка (x3;y3), на прямой проходящей через точки (x1;y1),C(x2;y2) >

program z20;
uses crt;
var x1,x2,x3,y1,y2,y3 : real;
begin
clrscr;
write(‘x1=’);readln(x1);
write(‘y1=’);readln(y1);
write(‘x2=’);readln(x2);
write(‘y2=’);readln(y2);
write(‘x3=’);readln(x3);
write(‘y3=’);readln(y3);
if (x3-x1)*(y2-y1)-(y3-y1)*(x2-x1)=0
then write(‘лежит’)
else write(‘не лежит’);
readln;
end.

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель!

Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.

Задача. Проверить, принадлежит ли точка отрезку.

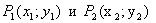
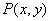
Пусть точки — начальная и конечные точки отрезка. — произвольная точка на плоскости.

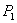
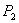
Вектор с началом в точке и концом в точке будет иметь координаты (x2-x1, y2-y1).

Если P(x, y) – произвольная точка, то координаты вектора 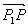равны: (x-x1, y – y1).

Точка Р будет принадлежать отрезку если:

Результаты выполнения программы.

Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.

Результаты тестирования в программе GeoGebra:

Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая — используется для проверки отношения «>=».

На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.

На этом я с вами прощаюсь. До встречи на следующем уроке.

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
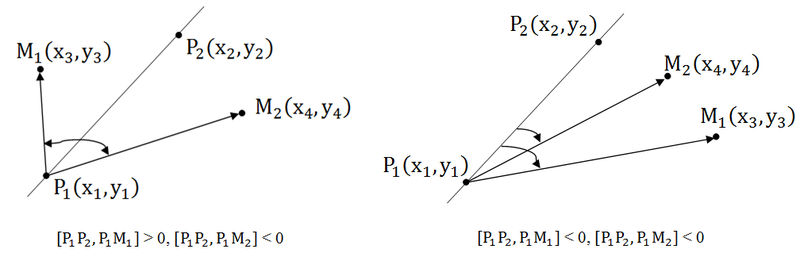
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
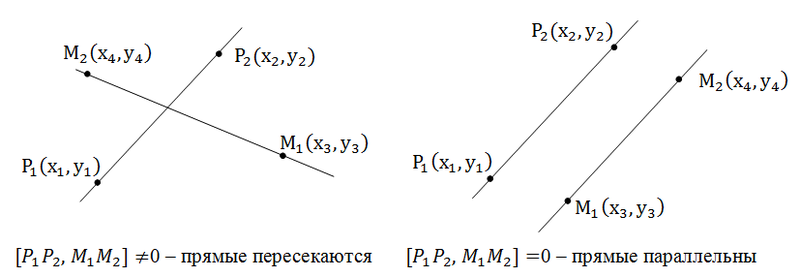
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
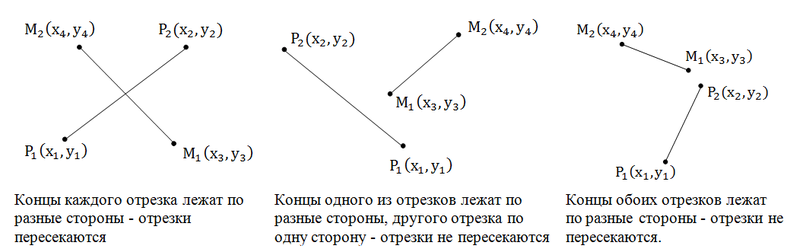
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
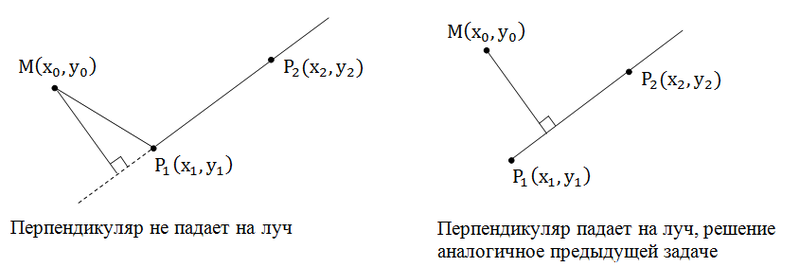
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

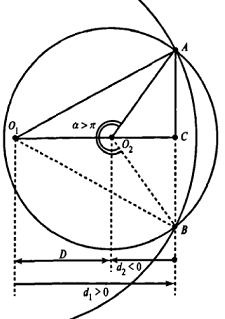
Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Источник

Точка и прямая

Точка и прямая являются основными геометрическими фигурами на плоскости.

Определение точки и прямой в геометрии не вводят, эти понятия рассматриваются на интуитивно-понятийном уровне.

Точки обозначают прописными (заглавными, большими) латинскими буквами: A, B, C, D, …

Прямые обозначают одной строчной (маленькой) латинской буквой, например,

Прямая состоит из бесконечного множества точек и не имеет ни начала, ни конца. На рисунке изображают только часть прямой, но понимают, что она простирается в пространстве бесконечно далеко, неограниченно продолжаясь в обе стороны.

О точках, которые лежат на прямой, говорят, что они принадлежат этой прямой. Принадлежность отмечают знаком ∈. О точках вне прямой говорят, что они не принадлежат этой прямой. Знак «не принадлежит» — ∉.

Например, точка B принадлежит прямой a (пишут: B∈a),

точка F не принадлежит прямой a, (пишут: F∉a).

Основные свойства принадлежности точек и прямых на плоскости:

Каковы бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и притом только одну.

Прямые также обозначают двумя большими латинскими буквами, по названию точек, которые лежат на прямой.

— эту прямую можно назвать MK или MN или NK.

Две прямые могут пересекаться и не пересекаться. Если прямые не пересекаются, они не имеют общих точек. Если прямые пересекаются, они имеют одну общую точку. Знак пересечения — ∩.

Например, прямые a и b пересекаются в точке O

(пишут: a ∩ b=O).

Прямые c и d также пересекающиеся, хотя на рисунке нет их точки пересечения.

Прямые m и n не имеют общих точек.

Источник

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Источник