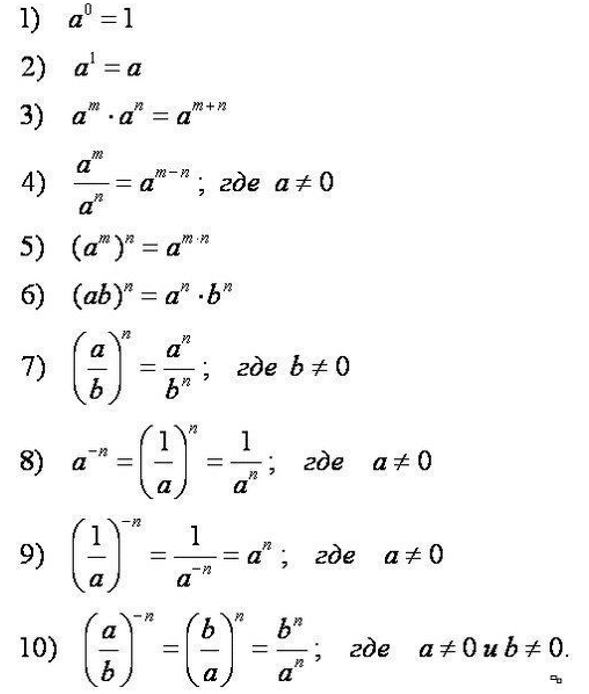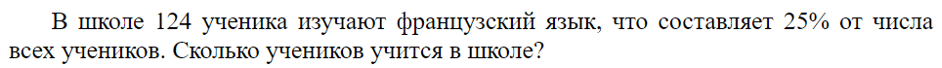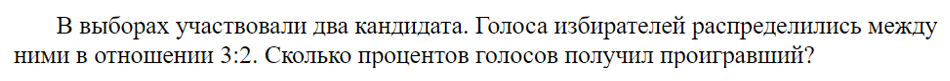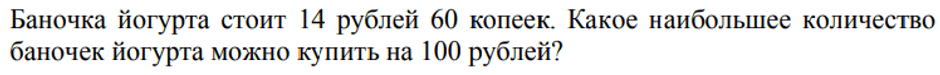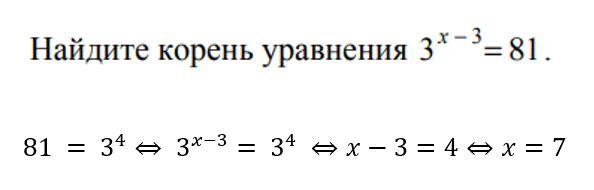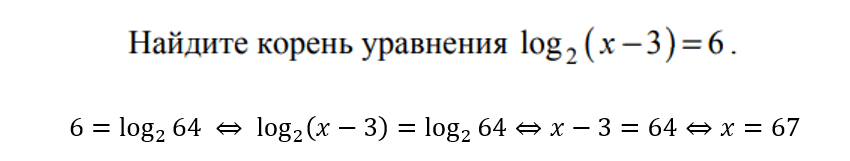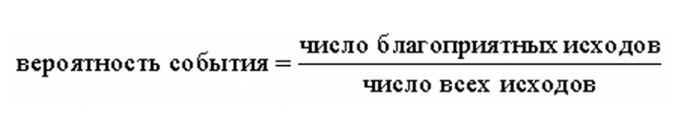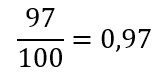Математика база это что
Какая математика нужна? Отличия профильного и базового уровня
В 11 классе школьникам предстоит сделать выбор, какую математику сдавать на ЕГЭ – профильную или базовую. Сегодня мы поговорим о том, чем один уровень отличается от другого, и для чего было сделано такое разделение.
Что такое базовая математика?

Базовый экзамен по математике оценивается по 5-балльной шкале (набранные баллы переводятся в привычные оценки), состоит из 20 заданий и охватывает всю школьную программу с 1 по 9 классы. Они относительно простые, и для того, чтобы получить тройку, нужно решить правильно всего 7 заданий, как это было, например, в 2017 году.
Вот что входит в базовый уровень:
С 1 по 16 задания относительно простые, с 17 по 20 – по сложности можно сравнить с профильным уровнем. Кроме того, задачи базового уровня не требуют подробно описывать ход решения.
Что такое профильный уровень?
И еще несколько советов от преподавателей нашего центра.
В отличие от базовой математики, профильная оценивается по 100-балльной шкале. На данный момент минимальный балл – 27, но ближе к экзаменам ситуация может измениться.
Какая математика нужна в вузе?
Если в перечне вступительных испытаний указана математика, вам нужно будет сдавать профильный уровень. Имейте в виду, данное уточнение есть не во всех положениях о приеме абитуриентов, считается, что это общеизвестный факт. Даже если вы сдали базовую математику на максимальный балл, в приемной комиссии этот результат принят не будет.
Профильная математика нужна не только технарям и физикам. Она требуется на некоторых гуманитарных направлениях, особенно, если они связаны с экономикой, управлением, лингвистикой и другими общественными науками.
Что выбрать, чтобы наверняка сдать?
Основной совет: трезво оценивайте свои возможности. Например, если вы перебиваетесь с двойки на тройку, то лучше не мучиться и написать на высокие баллы базовую математику и получить хороший аттестат, чем потерпеть полное фиаско, выбрав профильный уровень.
В случае, когда этот предмет нужен, чтобы поступить в вуз мечты, но с ним вы не дружите, то хотя бы начинайте подготовку к ЕГЭ не за год, а за два. Пробелы в знаниях формировались несколько лет и за 8 месяцев подготовки вы их не восполните.
К профильной математике следует усердно готовиться, даже если у вас по ней твердая пятерка. На экзамене может случиться разное, например, вы переволнуетесь, растеряетесь и всё забудете. Нужно быть во всеоружии. Пройдите под руководством опытного преподавателя типовые экзаменационные задания, чтобы выработать автоматический навык.
Базовая и профильная математика: отличия
Ксения Крашенинникова
Термины «математика-профиль» и «математика-база» давно понятны каждому выпускнику — такое разделение существует уже три года, поэтому программы подготовки и к тому, и к другому экзамену давно разработаны и активно применяются. Тем не менее, такое «раздвоение» математики до сих пор вызывает у школьников и родителей непонимание: к чему готовиться — к базовой или профильной математике?
Разница Базы и Профиля #1
Первое отличие базовой и профильной математики заключается в системе оценок. Профильная математика оценивается, как и все ЕГЭ, по стобалльной шкале. Порог, который требуется перешагнуть, — 27 баллов.
Базовая же математика оценивается «по-школьному»: максимальный балл для «базовика» оценивается в пять баллов. В этом случае школьнику достаточно получить тройку, чтобы сдать экзамен. И подготовиться к ней не так сложно.
Хотите круто подготовиться к экзаменам? Записывайтесь на бесплатный пробный урок в MAXIMUM! Вы узнаете всю структуру ЕГЭ, разберете сложные задания из первой части, получите полезные рекомендации и узнаете, как устроена подготовка к ЕГЭ в MAXIMUM.
Разница Базы и Профиля #2
Второй момент, отличающий профиль и базу, связан с самой структурой заданий. «База» не предполагает развернутых решений. Экзамен состоит из двадцати заданий с краткими ответами и проверяет способность выпускника применять знания по математике в повседневности (начиная с расчета лампочек для люстр и заканчивая покупками в магазине).
Профильная же математика состоит из двух частей и, разумеется, в разы сложнее. Первая часть состоит из двенадцати заданий, вторая – из семи. Здесь на проверку знаний школьной программы 10-11 классов отведено пять задач, а завершают экзаменационные КИМы две задачи олимпиадного уровня.
Олимпиадные задания не входят в школьную программу и должны быть освоены самостоятельно или с помощью репетитора.
Разница Базы и Профиля #3
Третье различие двух ЕГЭ по математике —разница приема в вузы. Так, если вы собираетесь поступать на специальность, которая требует среди обязательных экзаменов математику, придется сдавать «профиль».
Для поступления на направления, не требующие результатов по математике (как правило, это гуманитарные специальности), достаточно сдачи «базы», которую, к слову, можно по желанию сдать в десятом классе.
Для тех, кто мечется между «базой» и «профилем» с 2019 года никаких компромиссов нет: выпускник обязан выбрать только один экзамен.
Вы можете сдать и тот, и другой экзамен только с разницей в один год. Именно поэтому есть смысл сдать «базу» в 10-м классе, а «профиль» — в 11-м.
Базовая математика ЕГЭ
В 2016 году ЕГЭ по математике разделили на два уровня – профильный и базовый. Профильная математика – для тех, кто поступает на технические и экономические специальности. А базовая математика – экзамен для гуманитариев. Если баллы ЕГЭ по математике не нужны для поступления, достаточно сдать базовую математику ЕГЭ. Базового ЕГЭ по математике достаточно для получения аттестата Причем его намного проще сдать на высокий балл, чем профильную математику!
Чем отличаются эти экзамены?
Профильный ЕГЭ по математике – это 19 заданий, среди которых 12 – более простые, и оценивается в них только ответ. А вторая часть – 7 сложных задач. В них оценивается не только ответ, но и грамотное, обоснованное, правильное решение
В заданиях базового ЕГЭ по математике 20 задач, причем оценивается только краткий ответ, который определенным образом заносится в бланк.
Профильный ЕГЭ по математике оценивается по стобалльной шкале, минимальный балл 25-28, в зависимости от года. А базовая математика ЕГЭ оценивается по пятибалльной системе, как в школе, и минимальный балл 3 (тройка, не двойка, уже хорошо).
Кажется, что базовый ЕГЭ по математике сдать легко. Так ли это?
Во-первых, это 20 задач, причем никаких ответов «на выбор» в них не дается. Как много говорили о том, что ЕГЭ – это «угадайка», «глупый тест», и можно записать случайные ответы и получить пятерку. А попробуйте угадать 20 правильных ответов! Без знания математики – не получится.
И это значит, что надо решить 20 задач подряд. Нужно внимание, уверенность, умение быстро и правильно считать без калькулятора.
Во-вторых, задания взяты из всех тем школьной программы. Это не примеры типа «сколько будет дважды два?» Вот что входит в программу базового ЕГЭ по математике:
Преобразование алгебраических выражений, корни и степени, логарифмы, текстовые задачи на проценты, на движение и работу, теория вероятностей, геометрия, стереометрия, тригонометрия и даже такая тема, как производная! Да, это не «дважды два»!
Правда, вместе с вариантом базового ЕГЭ по математике вы получите необходимый справочный материал. Если вы гуманитарий и забыли формулы стереометрии или геометрический смысл производной, не расстраивайтесь – у вас это будет в справочных материалах. Важно только, чтобы вы не увидели все эти формулы впервые именно на экзамене.
И еще один важный момент. Расписание экзаменов обычно составляют так, что между базовым и профильным ЕГЭ всего один день. Поэтому тем, кто уверен в своих силах и знает, что сдаст профильный ЕГЭ на высокие баллы, можно заранее отказаться от базового ЕГЭ по математике.
Базовая математика ЕГЭ – это не сложно! Главное – вовремя вспомнить, что такой экзамен существует, и начать готовиться!
Быстро подготовиться к базовой математике — инструкция к каждому заданию
Антонина Белова
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Их выделили пометкой «Делаем обязательно», и таких заданий 10 штук. Как раз с запасом на ошибки.
Для тех, кто хочет получить выше тройки, мы дали рекомендации по еще 4 задачкам. Итого мы рассмотрели 14 номеров. Стоит сделать их все, и твердая четверка у вас в кармане.
Научим решать сложные задания
ЕГЭ по математике
на пробном уроке в MAXIMUM
Задание 1 (Делаем обязательно!)
Задание проверяет базовые навыки счета, которым вы научились в 5-6 классах. Для получения балла надо:
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления простых и десятичных дробей. Мы лично знаем ребят, которые не могут правильно разделить десятичные дроби в 11 классе!
Задание 2 (Делаем обязательно!)
Задача чуть сложнее: пример со степенями. Для выполнения надо:
Нужная теория будет в справочных материалах на экзамене, но это не поможет, если не наработан навык ею пользоваться. Практика обязательна.
Задание 3
Составители экзамена проверяют ваш навык работы с процентами. Задачи на проценты бывают трех типов:
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:
Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13-ю процентами. Сколько это в рублях нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, делаем 3 шага:
А. Переводим процент в десятичную дробь
Для этого всегда надо количество процентов поделить на 100.
Б. Находим, сколько это от зарплаты в рублях
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число на эту дробь умножить.
12 500 * 0,13 = 1 625 (р.) — налог, который удержат с зарплаты Ивана Кузьмича.
В. Отвечаем на вопрос задачи
У нас просили зарплату после вычета налога, а не сам налог.
12 500 — 1625 = 10 875 (р.)
Будьте внимательны, многие завалятся именно на последнем шаге!
Тип 2. Найти число по его части
Прочувствуйте разницу с прошлой задачей: тут 124 это и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
А. Переводим процент в десятичную дробь
Б. Находим, сколько учеников всего
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (у.) — всего.
Тип 3. Найти, сколько процентов часть составляет от целого
Особенность подобных заданий — не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
А. Находим, какую долю новая цена составляет от первоначальной
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть на целое разделить.
Б. Переводим долю в процент
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100
0,85 * 100 = 85 % — столько процентов новая цена составляет от старой
В. Отвечаем на вопрос задачи
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной? Конечно, изначально она была 100%. Итого
Остался последний тип, не так явно связанный с процентами…
Тип 4. Задачи на соотношение
Если чуть перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они ОДИНАКОВЫЕ по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
А. Считаем общее количество частей
Б. Узнаем, сколько голосов составляет одна такая часть
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит каждая из пяти частей «весит»…
В. Отвечаем на вопрос задачи
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
Решение этих задач удобнее всего оформить табличкой
| 1 кандидат | 2 кандидат | Всего | |
| Части | 3 | 2 | 5 |
| Абсолютные величины | 20% * 2= 40% | 100 % |
1 часть = 100% : 5 = 20%
Если рассчитываете решать текстовую задачу, включите здравый смысл! Ответ всегда можно проверить на адекватность благодаря обычной логике. Без нее и выстроить ход решения выйдет вряд ли.
Задание 4 (Делаем обязательно!)
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
Самое трудное тут — правильно выразить искомую величину: повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе часто эта задача проста настолько, что даже перекидывать ничего не придется, нужная величина уже будет слева от равно.
Задание 5
Задачка чуть сложнее: придется поработать с выражением. Чтобы точно получить балл, надо подготовиться ко всем возможным вариантам номера. Чтобы сдать базовую математику, нужно повторить и, самое главное, научиться применять:
Да, почти вся эта теория будет у вас на экзамене в справочных материалах, но еще раз: не надейтесь грамотно ею воспользоваться без наработанного навыка.
Задание 6 (Делаем обязательно!)
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.
Если ходите в магазин с карманными деньгами, то сталкиваетесь с подобными задачами каждый день! Разделим 100 рублей на стоимость одной упаковки йогурта. Не забываем приводить все величины к одной размерности:
Так сколько баночек йогурта вам продадут? На 7 штук вам явно не хватает денег, значит округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Одна пачка на 6 рулонов, значит на 63 рулона:
Но опять же, никто полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на 3 последние рулона. Значит округлить надо в большую сторону, взять клей с небольшим запасом. Снова математическое правило округления игнорируем.
Задание 7 (Делаем обязательно!)
Хотите сдать базовую математику — вам повезло! В номере с уравнениями не попадется тригонометрического. Зато могут быть..
Раскрываем скобки, если они есть, слагаемые с «х» переносим в одну сторону от равно, без «х» — в другую. Приводим подобные и решаем простейшее уравнение.
Бывают полные и неполные, всего надо повторить 3 алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений (ОДЗ): подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
Чуть веселее. Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:
Еще чуть веселее. С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.
Тут тоже могут быть особенности с ОДЗ. Проверяйте подстановкой.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо икса в уравнение! Не забывайте проверять, ведь это возможность убедиться на 100%, что заветный балл не проплывет мимо. Только так можно уверенно сдать базовую математику.
Задание 9 (Делаем обязательно!)
Задача на здравый смысл. Нужно соотнести величины с их возможными значениями.
Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек 8 тонн.
Главное — внимательно перенести ответы в бланк.
Задание 10 (Делаем обязательно!)
Простая задача на определение вероятности.
Решаем с помощью формулы:
Внимательно читаем вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит остальные в порядке, и нам подойдет любая из оставшихся 97 штук. Это и есть наши благоприятные исходы из формулы.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит ответ у вас выйдет некрасивый, но вы его «причЕшите» округлением.
Еще один подвох: формулировка с предлогом «на». К примеру, «на 100 лампочек 3 неисправны, найдите вероятность купить неисправную». Подходящие исходы даны тут явно: 3 неисправные лампочки. А вот число всех исходов спрятано и составляет 103, потому что «на».
Всегда есть вероятность, что вам не повезет, и попадется задачка с перебором подходящих вариантов… Тема довольно объемная, можете изучить ее самостоятельно или надеяться на удачу.
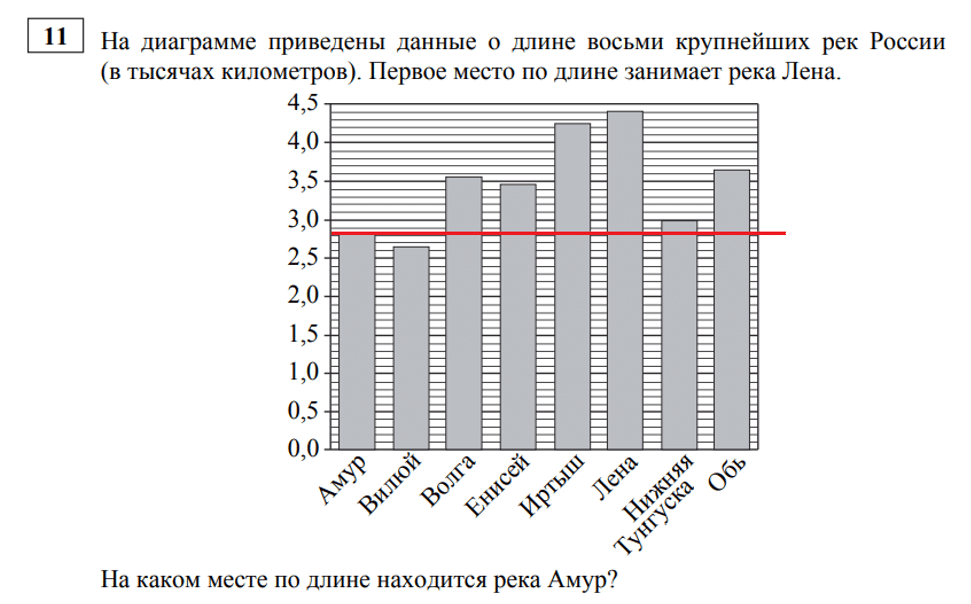
Задание 11 (Делаем обязательно!)
Задание на работу с графиком, диаграммой или таблицей, и не выполнить его вы просто не имеете права! Вооружайтесь карандашом, читайте условие с предельной внимательностью, безжалостно отмечайте нужные по условию значения на картинке в КИМе. Мы серьезно, вы и представить не можете, сколько народу теряет тут баллы по невнимательности.
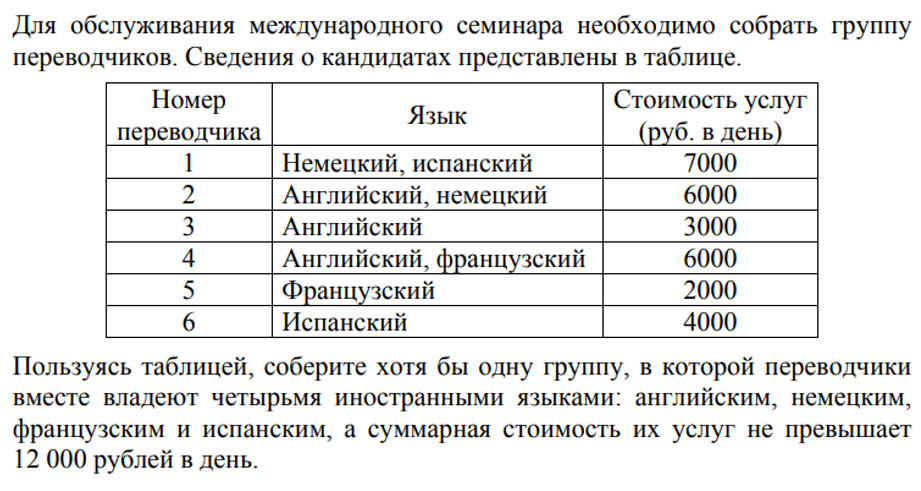
Задание 12 (Делаем обязательно!)
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
Задание 14
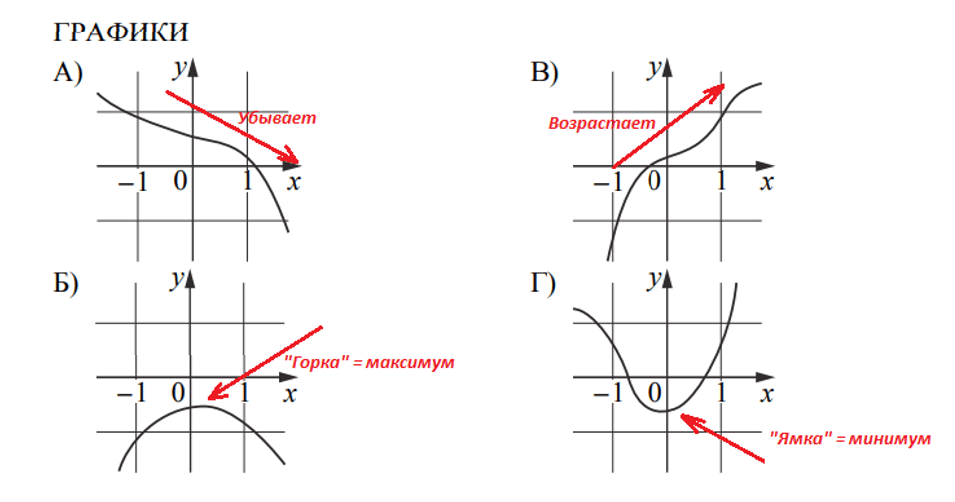
В номере точно понадобится навык анализа поведения функции по графику.
Запомним: точка максимума будет на «горке». Точка минимума — в«ямке». Функция убывает, если идёт вниз слева направо. Возрастает, если идёт вверх слева направо.
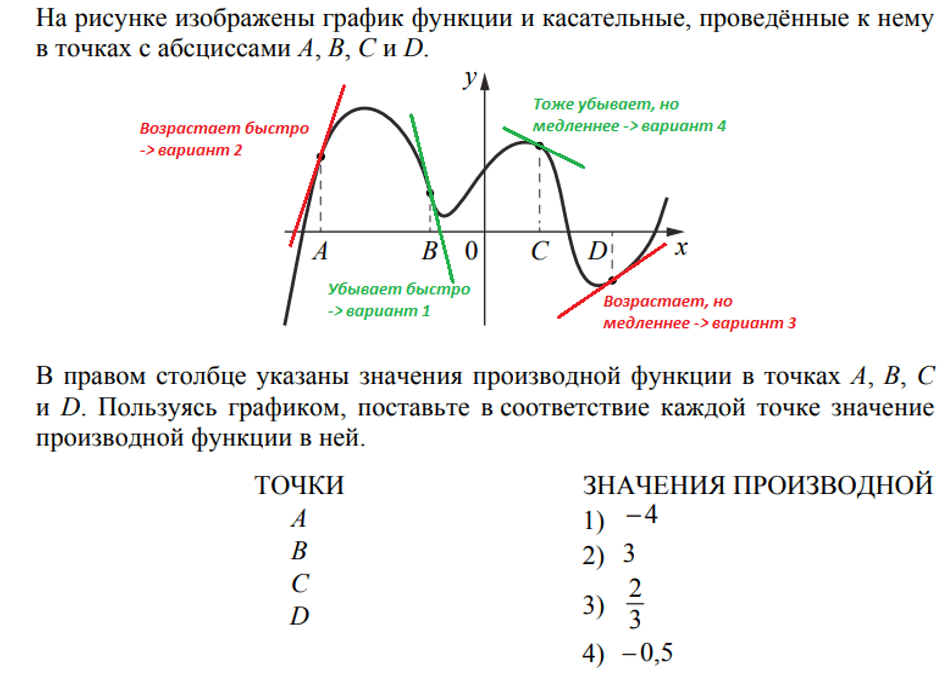
Если не повезет, то придется вспомнить азы теории по производной.
Здесь всё дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает – отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
Задание 18 (Делаем обязательно!)
Задача проверяет у ребят, которые хотят сдать базовую математику, умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.
Все, что от вас требуется – схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно! Не додумывайте какие-то дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
А бывают случаи, когда с визуализацией задачки придется постараться.
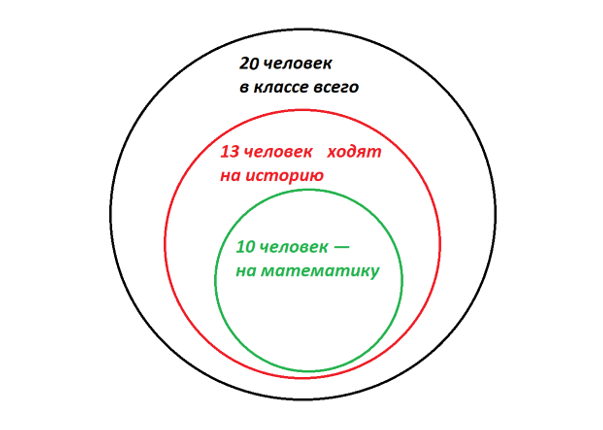
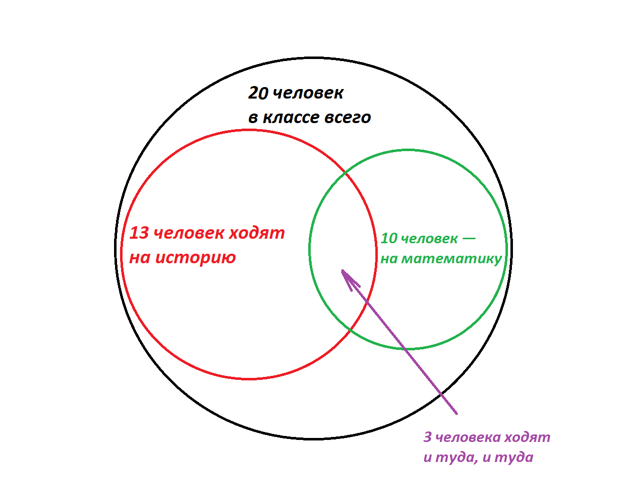
Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам?
Конечно, возможны еще какие-то промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
Так что для решения иногда мало логики, понадобится еще чуток воображения. Потренируйтесь, и ваши шансы получить балл повысятся.
Задание 19
Чем дальше, тем интереснее становятся задачи. Этот номер уже напоминает олимпиадную задачку, правда для средней школы.
Если хотите сдать базовую математику и решить 19 номер, надо немного познакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте, если время на ЕГЭ позволяет.
Например, тут нам помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на разные множители, признак для которых есть. Например, это:
Эти несложные закономерности гугл выдает по первому же запросу. Их немного: на 2, 3, 4, 5, 8, 9, 10, 11. Вполне посильная задача для выпускника.
Начнем с признака для четырех. Пока что наше число заканчивается на 13. На 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну. Теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для трех: 7+5+1+5+7+6 = 31. Какое ближайшее число разделиться на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576. Конечно, это не единственное решение.
А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив семь заданий (или больше, конечно!). Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов и методы решения к ним не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: 8, 13, 15, 16. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой.
Задание 17 обычно, хоть и не всегда, содержит неравенство. Это отдельный большой блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет, и попадется задачка на расположение значений на числовой прямой.
Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что семь третьих больше двух, но меньше трех. Корень из 26 равен пяти с копейками, а отрицательная степень сделает из трех пятых пять третьих или чуть больше полутора. Подобные задания надо пытаться делать обязательно!
Задание 20. Здесь попадаются разные типы неочевидных задач на логику. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 20 номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!