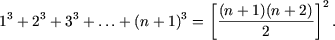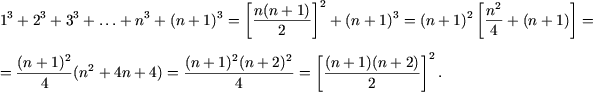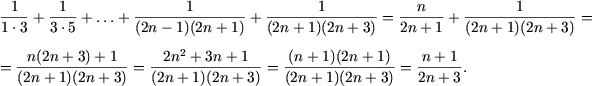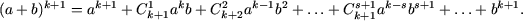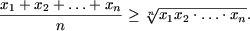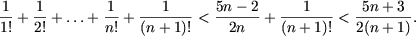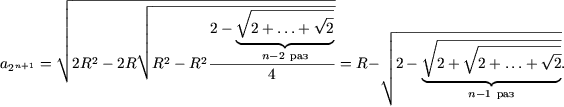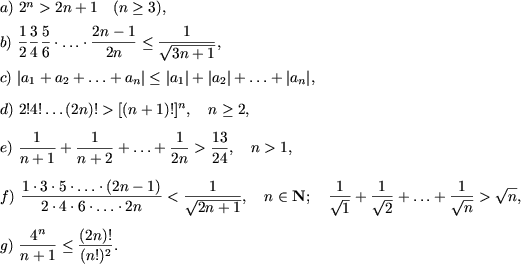Методом математической индукции доказать что для любого натурального n справедливо равенство
Методом математической индукции доказать что для любого натурального n справедливо равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Методом математической индукции доказать что для любого натурального n справедливо равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 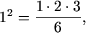
d) При n = 1 равенство справедливо: 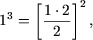
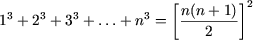
e) Утверждение P(1) справедливо: 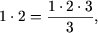
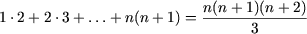
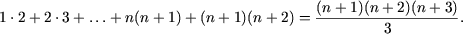
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 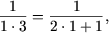
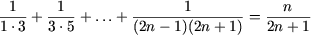
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
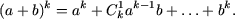
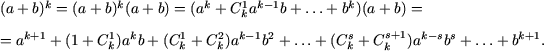
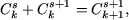
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
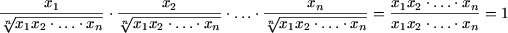
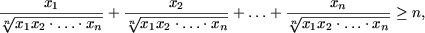
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 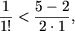
Допустим, что 
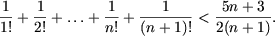
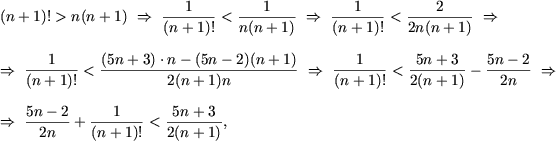
Поскольку при n > 10 имеем 
Пример 3. Доказать, что для любого n О N

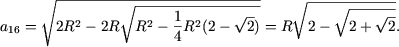
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
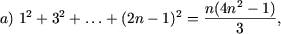 |
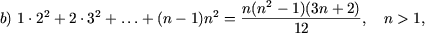 |
 |
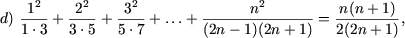 |
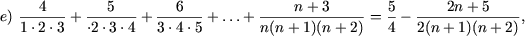 |
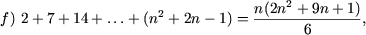 |
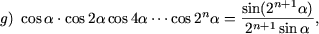 |
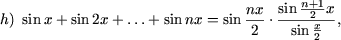 |
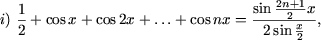 |
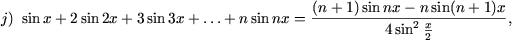 |
 |
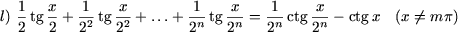 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 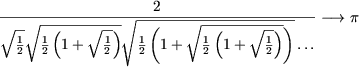
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Основы метода математической индукции
Доказательство с помощью метода математической индукции проводится в два этапа:
Метод математической индукции применяется в разных типах задач:
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
Задача 9. Доказать неравенство:
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму
Заказать решение
Полезные ссылки о ММИ
Кратенький видеоурок о ММИ
Примеры по теме «Математическая индукция»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Пример 1. Найти сумму S n первых n нечетных чисел:
В таких ситуациях обычно начинают рассматривать частные случаи:
S 4 = 1 + 3 + 5 + 7= 16; S 5 = 1 + 3 + 5 + 7 + 9 = 25.
Какой вывод можно сделать на основе этих частных случаев? В данном случае высказать гипотезу несложно:
сумма первых п нечетных чисел равна квадрату их числа, т. е. квадрату числа складываемых нечетных чисел: S n = п 2 .
Пример 2. Пусть требуется найти
для каждого натурального п.
Рассмотрим частные случаи: S1 = 3, S 2 = 18.
Попробуем доказать справедливость этого утверждения методом математической индукции.
S 1=1 • 3 = 3 • 1 ·(2 • 1-1) — равенство верно.
2. Индуктивное предположение: Пусть формула
верна для некоторого произвольного k > 1.
3. Индуктивный переход. Надо доказать справедливость равенства
S k +1=3 k (2 k –1) + (2 k +1)(2 k + 3) = 10 k 2 + 5 k + 3,
но нам нужно было получить
S k +1 = 3( k + 1)(2 k + 1) = 6 k 2 + 9 k + 3.
Так как у нас получился иной результат, то высказанное предположение неверно; на самом деле справедлива формула
Пример 3. Доказать, что при любых натуральных п число 7 n + 12п+ 17 делится на 18.
1. При n = 1 число 7 1 + 12 • 1 + 17 = 36 кратно 18.
2. Предположим, что для некоторого натурального числа k ≥ 1 число
7 k + 12 k + 17 делится на 18.
3. Рассмотрим число 7 k +1 + 12( k + 1) + 17 и докажем, что оно кратно 18.
Мы видим, что при любом натуральном k число 6 • 12 k + 90 = 18(4 k + 5)
кратно 18. Итак, мы представили число 7 k +1 +12( k + 1) + 17 в виде разности двух чисел, каждое из которых делится на 18. Следовательно, и
само число 7 k +1 + 12( k + 1) + 17 кратно 18.
(32 > 25), значит, утверждение А(5) верно.
3. Индуктивный переход. Докажем справедливость неравенства
Запишем последнее неравенство в виде
т. е. требуемое неравенство.
Итак, согласно принципу математической индукции данное неравенство справедливо при всех натуральных n > 4.
Пример5.Доказать, что при всех натуральных п справедливо
В данном случае проверим наше неравенство для п = 1 и п = 2.
1. При п = 1 неравенство 4 1 > 7 • 1-5 верно. При п = 2 имеем
4 2 > 7 • 2-5 также верное неравенство.
Но при любом k ≥2 число
Следовательно, справедливо неравенство
Из неравенств (1) и (3) следует неравенство
Теперь, пользуясь принципом математической индукции, данное утверждение справедливо для всех натуральных чисел.
Замечание. В данном случае базис индукции — пункт 1 — содержит доказательство данного утверждения для первых двух натуральных чисел n = 1 и n = 2. Это связано с тем, что неравенство (2) не выполняется при k = 1, но справедливо при каждом натуральном k > 1. Поэтому, доказав данное неравенство для n = 1и n = 2, в дальнейшем рассматривались числа k ≥2.
Пример 6. Доказать, что если для n положительных чисел а1, а2. а n ( n > 1) выполнено условие a 1а2. а n =1, то
Предположение индукции. Пусть данное утверждение справедливо для всех
3. Индуктивный переход. Докажем, что если произведение k + 1 положительных чисел равно 1, т. е. а1а2. а k +1= 1, то их сумма не меньше количества слагаемых:
Отметим, что если все данные числа равны между собой, то каждое из них равно 1 и неравенство (6), очевидно, выполняется. Предположим, что хотя бы одно из заданных положительных чисел меньше 1, например, 0 a k +1 k > 1 (если какие-то другие два числа обладают указанными свойствами, то мы просто их перенумеруем).
Рассмотрим произведение k чисел: а1, a 2. а k -1( a k a k +1) = 1. По условию все эти числа положительны:
значит, по предположению индукции имеем
Чтобы доказать неравенство (6), перепишем неравенство (7) следующим образом:
Для доказательства неравенства (6) осталось доказать, что
Левую часть последнего неравенства можно записать так:
Тогда неравенство (8) с учетом (9) примет вид
Исследовательская работа по теме:» Метод математической индукции»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Понимание и умение применять принцип математической индукции является хорошим критерием зрелости, которая совершенно необходима математику. А. Н. Колмогоров
Со времен зарождения жизни человечество стремилось к прогрессу, и свои первые шаги оно начинало с каменного века. Постепенно мир усовершенствовался и изменился. Каменный век перешел в мультимедийный. Даже несколько десятков лет тому назад мы не могли предположить о таких глобальных переменах. Но, несмотря на все изменения, произошедшие за это время, есть вещи, которые не меняются и их ценность со временем не убывает. Всем, например, известно, что Земля круглая, что 2·2=4. К таким ценностям можно отнести и математическую индукцию.
Математическую индукцию можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.
Что такое индукция? В чем заключается метод математической индукции? Кто создал? Применение Что такое принцип математической индукции? Заключение
Применение Применение метода математической индукции при решении задач на делимость. Доказательство тождеств с помощью метода математической индукции Метод математической индукции в применении к другим задачам. Применение метода математической индукции к доказательству неравенств Метод математической индукции при решении геометрических задач
Полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев. Иногда общий результат удается предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция). Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. О применении в математике неполной индукции, в качестве метода доказательства, предостерегал ученых П. Ферма в одном из своих писем:
«…можно было бы предложить такой вопрос и взять такое правило для его решения, которое подходило бы для многих частных случаев и все же было бы на самом деле ложным и не всеобщим…». Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин. Пьер Ферма
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n ≥ p, где p- фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом. Если предложение А(n) истинно при n = p и если А(k) => А(k + 1) для любого k ≥ p, то предложение А(n) истинно для любого n ≥ p.
На сформулированном принципе математической индукции основан метод доказательства, называемый методом математической индукции. Доказательство по методу математической индукции проводится следующим образом: сначала доказываемое утверждение проверяется для n = 1, то есть устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным переходом.
В этой части доказывают справедливость утверждения для n = k + 1 в предположении справедливости утверждения для n = k (предположение индукции), то есть доказывают, что А(k) => А(k + 1). Замечание. Отметим, что оба шага в доказательстве методом математической индукции очень важны, ни один из них нельзя пропускать.
Математической индукцией фактически пользовались еще некоторые древнегреческие ученые. Однако впервые он был явно выражен Герсонидом в 1321 году. Характеристика принципа математической индукции содержится у широко образованного итальянского математика ХVI века Ф.Мавролико, переводчик Архимеда.
Архимед (287 до нашей эры – 212 до нашей эры) – древнегреческий математик, физик, механик и инженер. Сделал множество открытий в геометрии, заложил основы механики и гидростатики, автор ряда важных изобретений.
В « Трактате об арифметическом треугольнике» Б. Паскаль доказывает закон образования членов этого треугольника методом математической индукции. После этого метод начинает постепенно привлекать внимание некоторых ученых, в частности Бернулли.
Лишь со второй половины ХIХ века, после трудов Больцано, Коши, Гаусса, Абеля чисто индуктивные методы доказательств теряют значение в математике. На первый план выдвигается дедукция и математическая индукция. А. Коши (1789 – 1857) К. Гаусс (1777 – 1855) Н. Абель (1802 – 1829)
Пусть А(n) и В(n) – некоторые выражения. Доказать равенство А(n) = В(n) для любого натурального n по индукции можно так: Убедиться, что равенство А(1) = В(1) выполняется. Доказать равенство А(k + 1) – А(k) = В(k +1) – В(k). Теперь из предположения А(k) = В(k) и из равенства А(k + 1) – А(k) = В(k +1) – В(k) следует, что А(k + 1) = В(k +1). Тогда согласно принципу математической индукции доказываемое равенство верно для любого натурального n.
Пример 5. Методом математической индукции доказать справедливость равенства Доказательство: 1) пусть n = 1, тогда верно; 2) предположим, что при n = k справедливо равенство 3) докажем, что при n = k + 1 выполняется равенство
Для этого разделим равенство на равенство Имеем:
При n = 4, неравенство имеет вид (2). Докажем. Представим левую часть неравенства в виде Умножим обе части неравенства на Имеем: На основании частного случая (1) рассмотрим правую часть неравенства
Следовательно, на основании метода математической индукции, неравенство Коши верно. Данное доказательство является классическим доказательством неравенства Коши. Обе части неравенства возведем в степень
Пример 5. Доказать неравенство для любого числа n корней, входящих в неравенство. Доказательство: 1) при n = 1 неравенство справедливо, так как 2) обозначим левую часть неравенства и, предположив справедливость неравенства докажем справедливость неравенства 3) Найдем: Следовательно, на основании метода математической индукции, неравенство верно.
III. Применение метода математической индукции в решении задач на делимость: Пример 1. Докажите, что для любого натурального n делится на 6. Пример 2. Докажите, что для любого натурального n делится на 19. Пример 3. Доказать при произвольном натуральном n делится на 26²(676) без остатка.
Пример 1. Докажите, что для любого натурального n делится на 6. Доказательство: 1) пусть n = 1, тогда 6 = 6; 2) предположим, что при n = k выражение 3) докажем, что при n = k + 1 выражение Так как и первое слагаемое, и второе слагаемое делятся на 6, то и их сумма делится на 6. Значит, на основании метода математической индукции при любом натуральном n делится на 6.
натуральном n Значит, на основании метода математической индукции при любом Так как каждое слагаемое делится на 676, то и сумма делится на 676. делится на 676.
IV. Применение метода математической индукции к геометрическим задачам: Задача 1. (Пересечение прямых) Докажите, что любые n прямых, расположенных на одной плоскости, никакие две из которых не параллельны, и никакие три не пересекаются в одной точке, пересекаются ровно в точках. Задача 2. Доказать, что число диагоналей выпуклого n –угольника равно Задача 3. Доказать, что сумма углов выпуклого n – угольника равна 180°(n – 2)
Задача 1. (Пересечение прямых) Докажите, что любые n прямых, расположенных на одной плоскости, никакие две из которых не параллельны, и никакие три не пересекаются в одной точке, пересекаются ровно в точках. Доказательство: 1) пусть n = 2, тогда утверждение верно, так как в случае, когда прямых две, известно, что они не параллельны, а значит, пересекаются в одной точке. 2) Предположим, что оно верно для n = k прямых, то есть что любых k прямых, никакие две из которых не параллельны, и никакие три не пересекаются в одной точке, пересекаются ровно в точках. 3) докажем, что при n = k + 1 прямых утверждение верно, то есть 1-я, 2-я, …, k-я прямая пересекаются в точках.
Рассмотрим (k + 1)-ю прямую и одну из прямых, обозначим её i из списка 1-я, 2-я, …, k-я прямая. Как мы уже доказали в шаге (1), что любые две прямые, удовлетворяющие условиям задачи, пресекаются ровно в одной точке, а значит и прямые (k + 1) и i пересекаются в одной точке. Вспомним, что i обозначает любую прямую из списка 1-я, 2-я, …, k. Отсюда (k + 1)-я прямая пересекается с каждой из этих k прямых ровно в одной точке. Рассмотрим список из (k + 1) прямых и их точек пересечения. Уберём прямую (k + 1) вместе с её точками пересечения. Останется k прямых удовлетворяющих шагу (3). Значит, количество точек пересечения у этих k прямых равняется Как было показано выше, количество точек пересечения, которое мы убрали вместе с прямой k + 1, равняется k. Следовательно, количество точек пересечения всех k + 1 прямых есть Следует, что для k + 1 прямых утверждение доказано.
Таким образом, число диагоналей в выпуклом (k+1)-угольнике равно Вследствие принципа математической индукции утверждение верно для любого выпуклого n-угольника.
Задача 3. Доказать, что сумма углов выпуклого n – угольника равна 180°(n – 2). Решение: 1) пусть n =3, тогда справедливо утверждение 180°(n – 2), так как 180°(3 – 2) = 180°; 2) предположим, что при n = k, утверждение 180°(k – 2) – верно; 3) докажем, что при n = k +1 сумма углов (k + 1) – угольника равна 180°(k – 1). В многоугольнике проведем диагональ Она разбивает многоугольник на многоугольник и треугольник Сумма углов многоугольника равна 180°(k – 2), а сумма углов треугольника равна 180°. Значит, сумма углов многоугольника
равна 180°(k – 2) + 180° = 180°(k – 2 +1) = 180°(k – 1). Вследствие принципа математической индукции теорема верна для любого выпуклого n-угольника.
Метод математической индукции в применении к другим задачам Задача 1. (Трехкопеечные и пятикопеечные монеты) Доказать, что любую сумму денег, большую 7 копеек, можно разменять только трехкопеечными и пятикопеечными монетами. (Ханойские башни) Задача 2. Есть три стержня и n колец разного размера. Класть можно только кольцо меньшего размера на кольцо большего размера. Можно ли переместить пирамидку с одного стрежня на другой? Можно или нельзя?
Задача 1. (Трехкопеечные и пятикопеечные монеты) Доказать, что любую сумму денег, большую 7 копеек, можно разменять только трехкопеечными и пятикопеечными монетами. Решение. Применим метод математической индукции к задаче. Пусть сумма равна n копейкам. 1) при n = 8 утверждение верно. 2) пусть утверждение верно для n = k. Могут представиться только два случая для размена суммы в k копеек:
Потребовались только трехкопеечные монеты 3) удаляем три трехкопеечные монеты, добавляем две пятикопеечные и тем самым размениваем сумму в копеек. Потребовалась хотя бы одна пятикопеечная монета 3) удаляем одну пятикопеечную монету, добавляем две трехкопеечные монеты и тем самым размениваем сумму в копеек. Следовательно, на основании метода математической индукции, задача верна.
Ханойские башни Есть три стержня и n колец разного размера. Класть можно только кольцо меньшего размера на кольцо большего размера. Можно ли переместить пирамидку с одного стрежня на другой? Можно или нельзя?
В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света. Количество перекладываний в зависимости от количества колец вычисляется по формуле 2ⁿ − 1. Для 64-х колец это 18 446 744 073 709 551 615 перекладываний, и, если учесть скорость одно перекладывание в секунду, получится около 584 542 046 091 лет, то есть апокалипсис наступит нескоро.
Подводя итог своей работы, я хочу сказать, что математическая индукция помогла мне научиться размышлять не только индуктивно, но и дедуктивно. Мое мышление преобразилось: я стала учиться размышлять логически, искать правильное решение из множества других. Знание и умение применять математическую индукцию помогло мне в решении олимпиадной работы: задание было на делимость. Аналогичные примеры есть у меня в докладе. В ходе моей работы было очень интересно собирать материал о математической индукции.
Понимание и умение применять принцип математической индукции является хорошим критерием зрелости, которая совершенно необходима математику. А. Н. Колмогоров
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Понимание и умение применять принцип
математической индукции является хорошим
критерием зрелости, которая совершенно
Со времен зарождения жизни человечество стремилось к прогрессу, и свои первые шаги оно начинало с каменного века. Постепенно мир усовершенствовался и изменился. Каменный век перешел в мультимедийный. Даже несколько десятков лет тому назад мы не могли предположить о таких глобальных переменах. Но, несмотря на все изменения, произошедшие за это время, есть вещи, которые не меняются и их ценность со временем не убывает. Всем, например, известно, что Земля круглая, что 2•2=4. К таким ценностям можно отнести и математическую индукцию.
Математическую индукцию можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.
Математической индукцией фактически пользовались еще некоторые древнегреческие ученые. Однако впервые он был явно выражен
Герсонидом в 1321 году. Характеристика
принципа математической индукции
содержится у широко образованного
ХVI века Ф.Мавролико, переводчика
В « Трактате об арифметическом треугольнике» Б. Паскаль доказывает закон образования членов этого треугольника методом математической индукции, после чего этот метод начинает постепенно привлекать внимание некоторых ученых,
методы доказательств теряют значение
в математике. На первый план выдвигается
дедукция и математическая индукция.
Несомненно, область применения
математической индукции возрастает,
несмотря на это, в школьной программе
ему отводится мало времени. Ну, скажите,
что полезного человеку принесут те два-три урока, за которые он услышит
пять слов теории, решит пять примитивных задач, и, в результате получит пятёрку за то, что он ничего не знает.