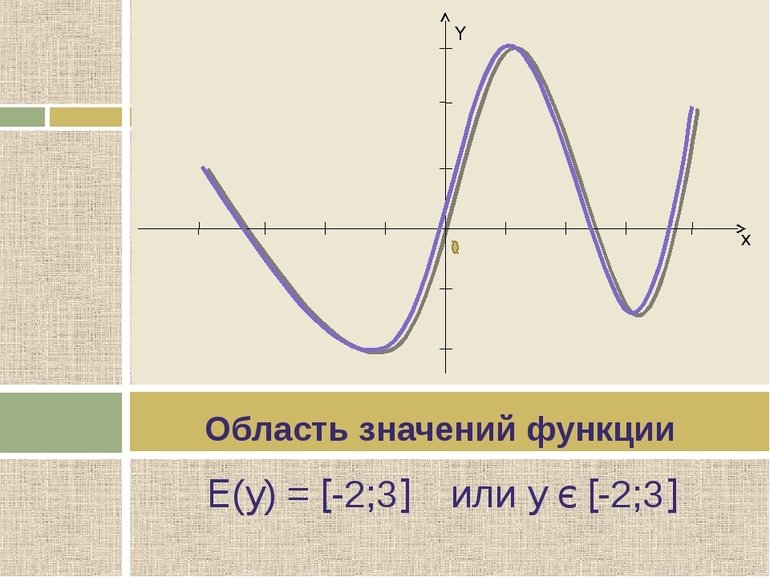
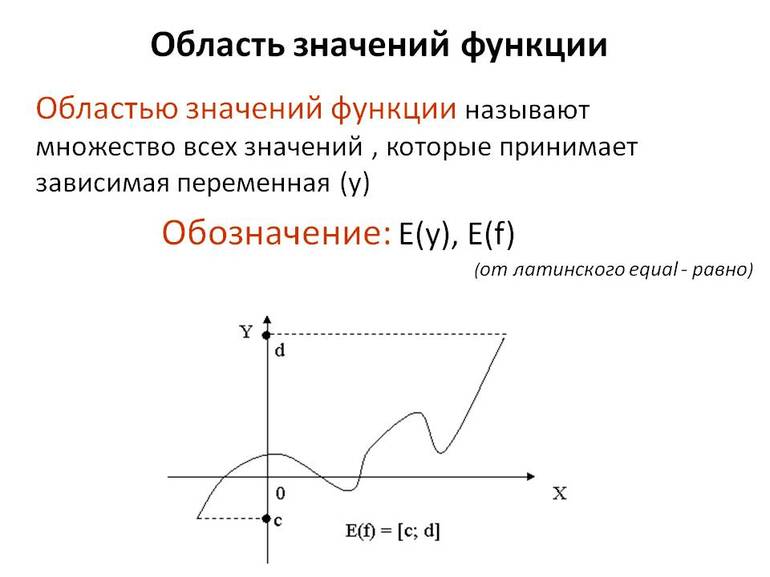
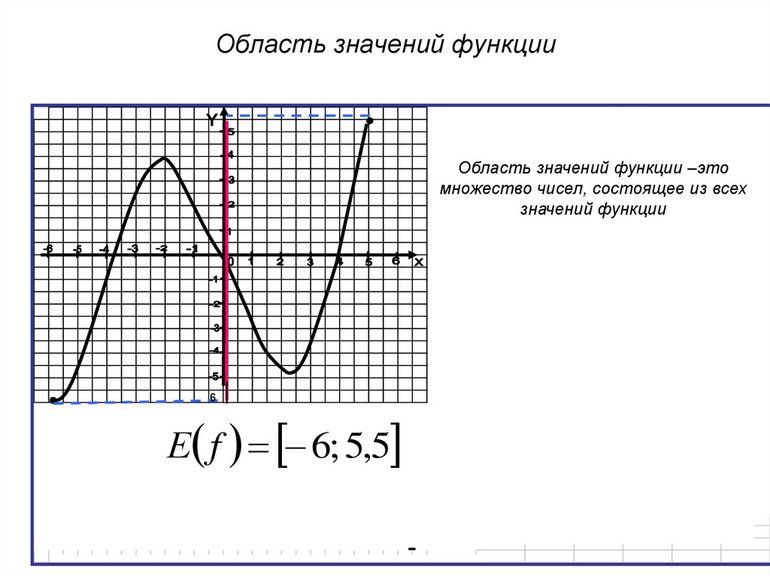
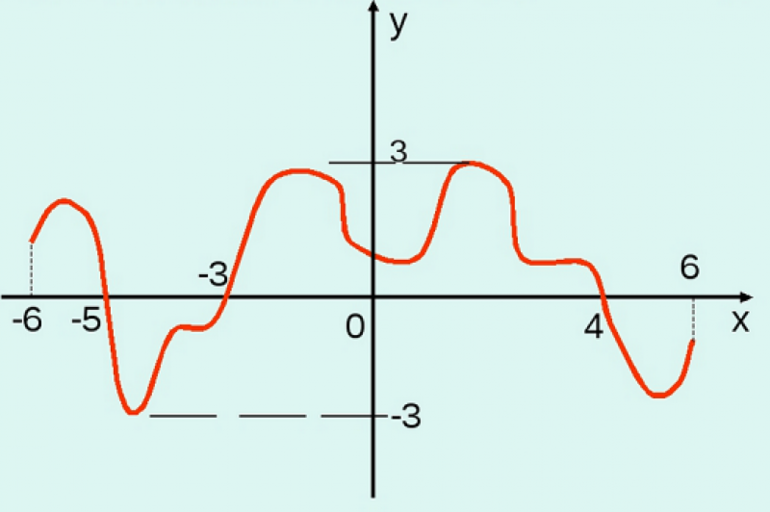
Множество значений что это

Нахождение множества значений функции.

1. Метод оценки (границ).

Для нахождения множества значений функции сначала находят множество значений аргумента, затем, используя свойства неравенств, отыскивают соответствующие наименьше и наибольшее значения функции функции. Если есть возможность путем тождественных преобразований получить функцию, которая на всей области определения или на заранее заданном множестве является непрерывной и либо только возрастающей либо только убывающей, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.

Пример 1. Найдите множество значений функци y=5 —.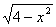

— 4— x 2 0.
Прибавим к трем частям неравенства 4 и получим

Множество значений функции y = 5 —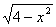является множество [3; 5].

Пример 3. Найти множество значений функции y = sinx + cos x.

Преобразуем выражение sinx + cos x = sinx +sin(— x) =
= 2sin((x +— x)/2)cos((x ++ x)/2) = 2sin<)cos(x +) =
=cos(x +).

-1cos(x +>1;

—cos( x +);

Так какданная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением, если таковые существуют, множество значений функции y =cos(x +) есть множество [-;]. Множество значений функции

y = sinx + cosx есть множество чисел [-;].

Пример 4. Найти множество значений функции y = 3sinx + 7cos x.

Преобразуем выражение 3sinx + 7cos x. Заметим, что 3 2 + 7 2 = 9 + 49 = 58 =Умножим и разделим каждое слагаемое на
3sinx + 7cos x =(sinx +cosx).
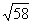
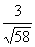
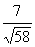
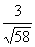
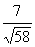
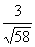
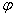
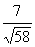
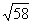
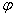
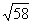
Так как 2 + () 2 = 1, то найдется такое числочто cos=и sin=. Тогда 3sinx + 7cos x =(cossinx + sincosx) =sin(+ x).

2. Метод применения свойств непрерывной функции.

Среди числовых значений, принимаемых на заданном отрезке непрерывной функцией, всегда имеется как наименьшее pначение m, так и наибольшее значение М. Множество значений функции заключено между числами m и M. Это основные утверждения положенны в основу поиска множества значений функции в следующем примере.

Пример 5. Найти множество значений функции y = 2sinx + cos2x на отрезке [0; p ].

D(y) = R. Данная функция на всей области определения непрерывна, поэтому на отрезке [0; p ] существуют такие точки, в которых функция принимает свои наименьше и наибольшее значения. Эти точки либо критические, либо концы отрезка.

1) найдем производную данной функции

3) Область определения производной R.

Отрезку [0;] принадлежат три критические точки: x =, x =, x =.

Вычисляем значение функции на концах промежутка и в критических точках:
y(0) = 1, y() = 1, y() = 1,5, y( ) = 1,5, следовательно, наименьшее значение функции на отрезке[0;] равно 1, а наибольшее значение функции на этом же отрезке равно 1,5. Исходя из выше изложенный утверждений Е(у) = [1; 1,5].

3. Метод приведения к уравнению относительно х с параметром у.

Возможна следующая схема применения этого метода:

Пусть функция задана формулой y = f(x).

2) Рассматриваем функцию как уравнение с параметром у.

Пример 6. найдите множество значений функции.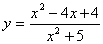

x 2 + 5 > 0 при любом х, следовательно, D(y) = R. Рассматриваем формулу:

1) Если у = 1, то данное уравнение равносильно линейному уравнению 4х + 6 = 0, которое имеет один корень.

Если у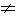1, то квадратное уравнение, которое мы получили в результате выше изложенных соображений, имеет корни тогда и только тогда, когда его дискриминант не отрицателен.

— 5y 2 + 4y +50;

Таким образом квадратное уравнение имеет корни,если параметр y[2-; 1) и (1; 2 +],

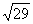
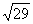
4. Метод непосредственных вычислений.

В случае, когда область определения функции содержит конечное число значений аргумента или количество значений не велико, или множество значений аргумента может быть описано с помощью конечного числа формул, так бывает в случае рассмотрения тригонометрических функций, обычно множество значений функции находят путем непосредственных вычислений.

Найдем область определения данной функции. Так как в формуле задающей функцию есть квадратный корень, то согласно определению квадратного корня потребуем, чтобы подкоренное выражение было неотрицательным:

Источник

Общая информация

У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.

Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.

В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.

Основные понятия

Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».

Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.

Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.

Типы функций

Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.

Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.

Важные свойства

Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:

Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.

Методы нахождения

Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:

Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.

Для каждого элемента

Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:

Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:

Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.

Оценочный способ

Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:

Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:

Производная, min и max

Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:

Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:

В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:

Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.

Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.

Источник

Область значения функции

Что такое функция в алгебре

Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.

Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.

Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).

Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается.

Область значений функции вместе с областью ее определения формирует границы для отображения данной функции в виде графика.

Виды функций

Для каждой функции, в зависимости от ее структуры, область значений будет своя. Рассмотрим основные виды элементарных математических функций.

Линейная

Область значений включает в себя все действительные числа: \(E(f)=(-\infty;\;+\infty).\)

Обратная пропорциональность

Квадратичная (квадратная)

Координата вершины \(y_0\) рассчитывается так:

Область значений зависит от коэффициента a:

Квадратную функцияю y=x^2 можно рассматривать как частный случай квадратичной или степенной функций. Так как при возведении числа в четную степень результат будет всегда положительным, область значений для нее следующая:

\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty) \)

Степенная

Область значений степенной функции зависит от того, к какому числовому множеству относится показатель степени n:

Показательная

\(\mathrm E(\mathrm f)=(0;\;+\infty) \)

Логарифмическая

\(\mathrm y=\log_<\mathrm a>\left(\mathrm x\right)\)

По своим свойствам логарифмическая функция обратна показательной. Для данных функций область определения и область значений меняются местами соответственно. ОЗ логарифмической функции включает в себя все действительные числа:

\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)

Тригонометрические

Рассмотрим четыре базовые тригонометрические функции:

Область значения тангенса и котангенса включает в себя все действительные числа:

\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)

Типы функций

При определении области значений функции необходимо учитывать ее фундаментальные особенности. Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.

Важные свойства

К наиболее важным для поиска области значений функции относят следующие ее свойства:

Методы нахождения

Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.

Перебор значений

Графический метод

Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.

Если по условию задачи необходимо найти область значений функции на определенном промежутке значений переменной x, то на графике максимальные и минимальные точки становятся очевидными. Это могут быть как общие точки экстремума, так и локальные максимальные и минимальные значения.

Учет непрерывности и монотонности

Данный метод вытекает из предыдущего и позволяет делать некоторые прогнозы об области значений функции исходя из ее свойств. Если на графике видно, что функция не прерывается и монотонно убывает или возрастает на определенном промежутке, можно предположить, что эта тенденция сохранится и дальше.

Например, график квадратичной функции f(x)=x^2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем \(x\in\lbrack-4;\;4\rbrack\) :

Рисунок 1. Значение непрерывности и монотонности функции для области определения

\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty)\)

Производная, min и max

Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.

Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.

Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:

Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:

Пример решения

Задача

Так как функция не относится к элементарным и по условию задачи область поиска не ограничена, воспользуемся методом нахождения точек минимума и максимума.

Найдем производную данной функции y’, воспользовавшись формулами из таблицы производных:

Согласно теореме Ферма, в точках экстремума производная равняется нулю.

Начнем решать полученное уравнение:

Так как уравнение равняется нулю, если хотя бы один из множителей равен нулю, разобьем его на три составляющие:

Получим следующие результаты:

Данные точки являются критическими. В итоге мы имеем четыре промежутка:

Чтобы понять, какие из точек являются минимальными и максимальными, необходимо взять по числу из каждого промежутка и решить производную \(y’=4\cdot x^3-4\cdot x \) относительно них. Сам результат вычислений не важен, учитывать нужно только знак: (+) или (-).

На первом и третьем промежутках производная принимает отрицательное значение, на втором и четвертом — положительное. Следовательно, найденные ранее точки \(x_1=-1\;и\;x_3=1\) являются точками минимума, а точка \(x_2=1\) — точкой максимума. Это еще не окончательный результат, так как необходимо понять, на каких промежутках функция возрастает, а на каких — убывает.

Область определения функции \(y=x^4-2\cdot x^2-5\) следующая:

Источник

Параграф 2. Повторение и расширение сведений о функции.

Работу выполнил: Косярский А.А. студент группы 45.2

Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

1. Понятие числовой функции

2. График функции

Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x
«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x

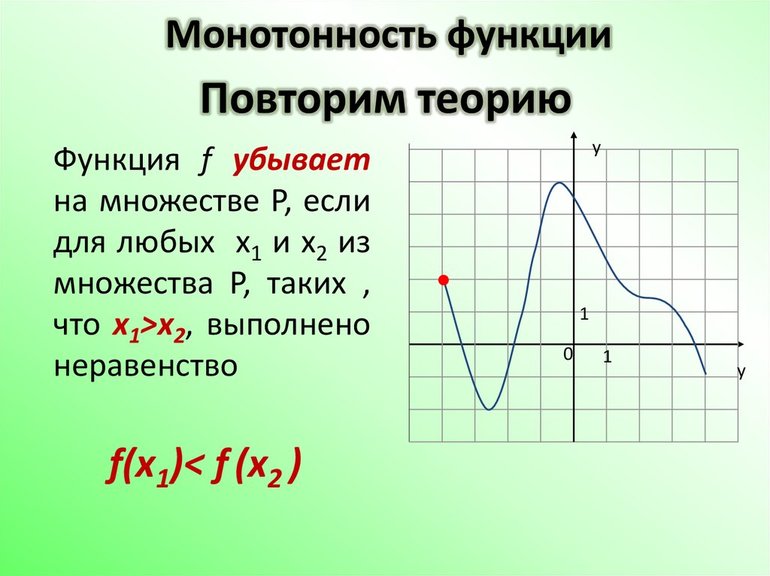
3. Возрастающие и убывающие функции

Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2)

4. Чётные и нечётные функции

Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy

Объяснение и обоснование

1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.

Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.

Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).

Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.

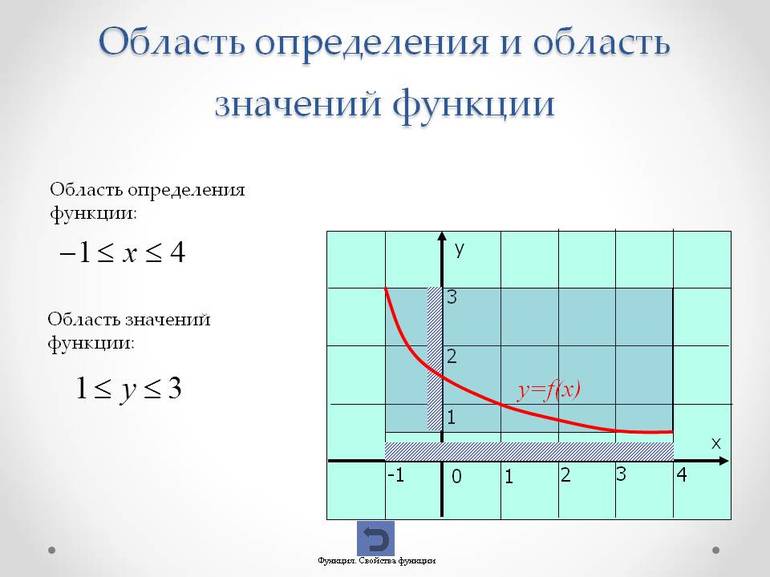
Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).

Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]

3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.

На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).

Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) x1 имеем
-2⋅

отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.

Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.

4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).

Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.

Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.

Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ:

ПРИМЕРЫ РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ

УПРАЖНЕНИЯ К ПАРАГРАФУ

5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x 5 5) y = √(x)

8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x 0

9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.

11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.

12. Обоснуйте, что заданная функция является чётной:
1) y = x 6 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x 4 )

Источник