Музыкальная цепочка что это
Музыкальные интервалы: какие они бывают и как их строить?
Интервалы в музыке – это расстояние между двумя звуками, и еще это созвучие двух нот. Вот такое простое определение можно дать этому понятию. На уроках сольфеджио интервалы поют и слушают, чтобы потом узнавать их в музыкальных произведениях, но сначала нужно научиться строить их от разных нот.
Простых интервалов всего восемь штук, они обозначаются обычными цифрами от 1 до 8, а называются особыми латинскими словами:
1 – прима
2 – секунда
3 – терция
4 – кварта
5 – квинта
6 – секста
7 – септима
8 – октава
Что означают эти названия? В переводе с латинского языка прима – первый, секунда – второй, терция – третий и т.д.
Интересные факты про названия интервалов
Многие из названий интервалов вам уже, наверное, не раз приходилось слышать, даже если разговор не касался музыки. Например, слово «прима» есть в словосочетании «примадонна» (так называют первую, то есть главную артистку-певицу театра).
Слово «секунда» очень напоминает английское числительное «second» (то есть второй), а название шестого интервала «секста» похоже на английское «six» (шесть).
Как строить интервалы от разных нот вверх и вниз?
Интервалы состоят из двух нот, которые могут быть расположены близко или далеко по отношению друг к другу. И о том, на каком расстоянии они находятся, нам говорит число интервала, которым оно обозначено (от 1 до 8).
Вы знаете, что каждый звук в музыке – это ступень большой музыкальной лестницы. Так вот число интервала показывает, сколько нужно пройти ступенек, чтобы от первого звука интервала добраться до второго. Чем больше число, тем шире интервал, и тем дальше его звуки друг от друга находятся.
Обратимся к конкретным интервалам:
Секунда – обозначается двойкой, потому что этот интервал охватывает уже две ступени: один звук находится на какой-либо ноте, а второй на соседней, то есть второй по счету ступени. Например: до и ре, ре и ми, ми и фа и т.д.
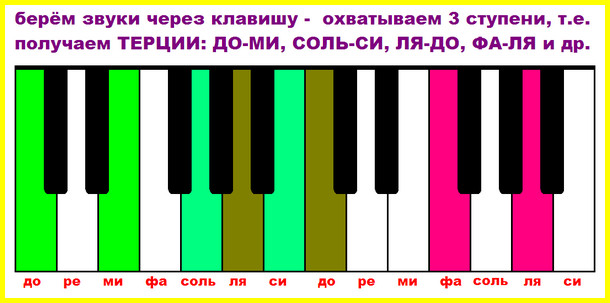
Терция – охватывает три ступени. Второй звук находится по отношению к первому на расстоянии трех ступеней, если идти подряд по музыкальной лестнице. Примеры терций: до и ми, ре и фа, ми и соль и т.д.
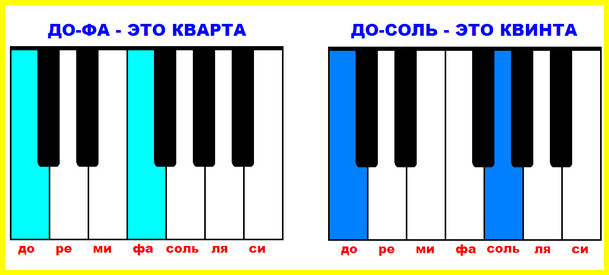
Кварта – теперь интервал расширяется до четырех ступеней, то есть первый звук находится на первой ступени, а второй звук – на четвертной. Например: до и фа, ре и соль и т.д. Поясним еще раз, что считать ступеньки можно начинать от любой ноты : хоть от до, хоть от ре – выбираем то, что нам нужно.
Квинта – обозначение числом 5 говорит о том, что ширина интервала – 5 ступеней. Например: до и соль, ре и ля, ми и си и т.д.
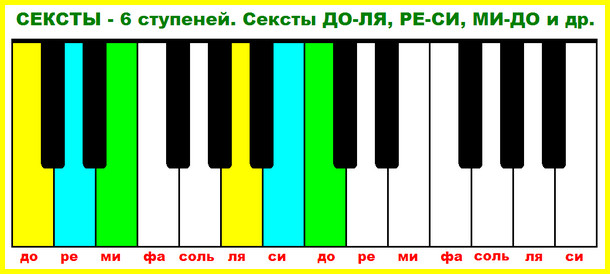
Секста и септима – числа 6 и 7, которыми они обозначаются, указывают на то, что нужно отсчитать шесть или семь ступеней, чтобы получить сексту или септиму. Примеры секст: до и ля, ре и си, ми и до. Примеры септим (все вверх по лестнице): до и си, ре и до, ми и ре.
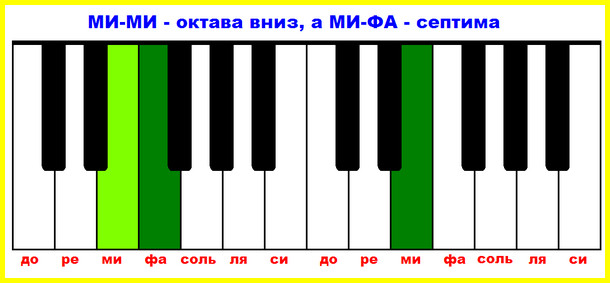
Октава – последний интервал, такой же легкий, как и прима. Это тоже повторение звука, только на другой высоте. Например: до первой октавы и до второй октавы, ре и ре, ми и ми и т.д.
А теперь давайте выстроим все интервалы по порядку от ноты ДО и ноты, например, СОЛЬ. Примеры можно послушать. Сделайте это!
Интервалы от ноты ДО вверх
Интервалы от ноты СОЛЬ вверх
Интервалы от ноты ДО вниз
Интервалы от ноты ЛЯ вниз
Упражнения : играем интервалы на фортепиано
При изучении интервалов одинаково полезны и взрослым, и детям упражнения на фортепиано или на нарисованной клавиатуре. Фортепиано или синтезатор со звуком, конечно, лучше, потому что цель изучения интервалов на сольфеджио – запомнить не название интервала, не ноты, которые его составляют (хотя это тоже важно), а звучание.
Поэтому если нет подходящего инструмента под рукой, то можно воспользоваться виртуальной клавиатурой или приложением «Пианино» на телефоне (планшете). Важно, чтобы вы работали не в немом режиме, а со звуком (желательно).
Упражнение 1. Играем примы
Примы играть легко, ведь прима – это повторение одной и той же ноты два раза. Значит, нужно просто два раза ударить по любой клавише и уже получится интервал. Прима – очень важный интервал, который встречается во многих песнях, поэтому никогда не нужно забывать о нем (забывают обычно потому, что он легкий).
Упражнение 2. Играем секунды
Секунду всегда образуют две соседние ступени, две ноты, которые находятся рядом. И на клавиатуре пианино, чтобы сыграть секунду, тоже нужно взять две соседние клавиши. Играйте секунды от разных нот – вверх и вниз, запоминайте звучание, можете также параллельно заниматься сольфеджио, то есть пропевать ноты, которые играете.
Упражнение 3. Играем терции
Терция – любимый интервал маленького В.А. Моцарта – гения мировой музыки. Известно, что в детстве Моцарт-малыш подходил к клавесину отца (инструмент – предшественник фортепиано), клавиши он не видел (по росту), но дотягивался до них ручками. Моцарт играл всякие созвучия, но больше всего радовался, когда ему удавалось «поймать» терцию – так красиво и мелодично звучит этот интервал.
Попробуйте поиграть терции и вы. Возьмите терцию «ДО-МИ» и запомните это расстояние: звуки расположены на клавиатуре через одну клавишу (через одну ступеньку). Играйте терции вверх и вниз от разных нот. Играйте звуки терций одновременно или поочередно, то есть вразбивку.
Упражнение 4. Играем кварты и квинты
Кварты и квинты – это интервалы, которые звучат воинственно, призывно и очень торжественно. Недаром с кварты начинается наш российский гимн. Возьмите кварту «ДО-ФА» и квинту «ДО-СОЛЬ», сравните их по звучанию, запомните расстояние. Играйте кварты и квинты от разных нот. Постарайтесь научиться мгновенно находить эти интервалы глазами на клавиатуре.
Упражнение 5. Играем сексты
Сексты, как и терции, тоже очень мелодичные и красивые по звучанию. Чтобы быстро сыграть сексту можно мысленно представить себе квинту (ее число 5) и добавить к ней еще одну ступеньку (чтобы было 6). Сыграйте сексты вверх «ДО-ЛЯ», «РЕ-СИ» и от всех других нот и вниз «ДО-МИ», «РЕ-ФА» и т.д.
Упражнение 6. Играем октавы
Октава – это повторение звука в следующей октаве. Вот такое вот парадоксальное и смешное определение можно дать этому интервалу. Найдите на клавиатуре две одинаковых ноты, которые расположены максимально близко: две ДО (одна в первой октаве, вторая – во второй), или две РЕ. Это и будут октавы. То есть октава – это расстояние от одного звука до его повторения музыкальной лестнице. Октавы нужно видеть сразу. Потренируйтесь.
Упражнение 7. Играем септимы
Чуть не пропустили седьмой интервал – септиму. Хотим поделиться с вами одной хитростью. Известно, что число октавы – 8, а септимы – 7. Значит, чтобы получить септиму, нужно всего-то вычесть одну ступеньку из октавы. Это способ быстрого построения септимы, чтобы не считать каждый раз семь ступеней «от печки».
Например: нам нужна септима от РЕ. Представим себе октаву – РЕ-РЕ, а теперь спустим верхний звук на одну ступеньку: получаем септиму РЕ-ДО!
Еще пример: построим септиму от МИ вниз. Отложили вниз октаву – МИ-МИ, а теперь, внимание, нижний звук поднимем на ступень вверх и получим септиму МИ-ФА вниз. А почему мы поднимали нижний звук, а не опускали? Потому что интервалы, построенные вниз, это как отражение в зеркале, и все действия потому нужно делать наоборот.
Дорогие друзья, если вы выполнили предлагаемые упражнения, то вы просто молодцы! Вы многое постигли, но это только начало, первое знакомство с интервалами. Интервалы в таком виде обычно проходят в 1-2 классах музыкальных школ, а потом все становится немного сложнее. И мы приглашаем вас отправиться за новыми знаниями вместе с нами.
В следующих выпусках вы узнаете, о том, что такое количественная и качественная величина интервала, что такое обращения и как можно получить уменьшенные и увеличенные интервалы. До новых встреч!
Природа музыкальных ощущений. Родство звуков
Этими статьями по теории музыки я ставлю задачу объяснить природу музыкальных ощущений человека. В последней статье будет рассмотрено веб-приложение для гармонического анализа музыки разработанное на основе этого исследования.
Начнём с физики. У каждого звука есть:
Тембр формируют обертоны — призвуки сопровождающие звук. Их рассмотрим подробнее.
Графический эквалайзер отображает обертоны звука в виде пиков. Шкала X-частота, Y-их громкость
Допустим колеблется вся струна с определенной частотой например 100 гц. Но природа так работает, что струна также начинает колебаться своими частями — половиной, третью, четвертью и т.д что образует новые звуки частотой выше. У половины частота в 2 раза выше основного тона, у трети в 3. Такие частоты образующие арифметическую прогрессию называют гармоническими обертонами или гармониками, остальные же будут — не гармоническими.
Природные обертоны как правило тише основного тона и чем выше они от него по частоте тем ниже их громкость.

При повышении частоты основного тона, обертоны пропорционально увеличивают свою частоту, поэтому высота звука прежде всего определяется нами по частоте первой гармоники(она же основной тон). Гармонические обертоны вместе с основным тоном называют натуральным звукорядом.
Гармоники, как самостоятельные колебания, образуют между собой соотношения частот – интервалы. Соотношение 2:1 — октава, 3:2 — квинта, 4:3 кварта и т.д к ним мы ещё вернёмся.
Интервалы образующиеся между двумя соседними по частотам обертонами звука
Эти соотношения слух воспринимает и расшифровывает благодаря чему среди множества одновременно звучащих звуков мы можем выделить конкретные тембры и определить источники звуков. Установлено что в мозге(в первичной слуховой коре) группы нервных клеток реагируют каждая на свою частоту с точностью вплоть до одного герца а также есть отдельный центр который занимается распознаванием сложных слуховых образов на основе соотношений частот, то есть интервалов, к примеру узнать тембр независимо от высоты, слова независимо от тембра.
Квинтовое родство звуков
Что роднит все природные музыкальные звуки так это присутствие ярко выраженных октавного и квинтового обертона в их тембре. Сравним звуки находящиеся на этих интервалах. Возьмем звук(верхняя половина), а затем октаву от него(нижняя половина рисунка ниже). Мозг понимает что такой звук, октаву, он уже слышал как самый громкий, первый обертон предыдущего звука(1 на верхнем рисунке). Частоты гармоник нового повторяют всё те же частоты старого, только пропорционально в 2 раза выше. Звуки на расстоянии октавы музыканты обозначают одной нотой(здесь это Bb).
После взятия квинты от Bb, звука F, возникает новый звук C как квинта от квинты
Вернемся к квинте. Мы связали нижний звук Bb со звуком на квинту выше F что уже содержался в первом звуке(2 на верхнем рисунке). Второй звук также имеет свой звук квинты(уже третий звук, C) и первый связан с ним опосредованно через 2ой. С каждым таким квинтовым шагом мы получаем новый интервал от первого звука до нового. Чем дальше мы удаляемся от первого звука тем отдаленнее связь с ним. С расстоянием связь теряется.
Квинтовая цепь звуков. Аудиопримеры
Цепь квинт на клавиатуре фортепиано. Квинту на нём можно отложить как 7 полутонов
Далее чуть ниже видео с аудиопримерами и таймкоды к нему чтобы вы могли эмпирически проверить приводимые утверждения.
Построим квартовый ряд от звука E и обнаружим, что звук Bb от которого мы строили квинтовый ряд снизу оказался наверху а верхний звук того ряда(Е) теперь внизу. То есть ряд кварт это просто перевернутый ряд квинт.
Квинтовый и квартовый ряд есть обращения по отношению друг к другу
Главные музыкальные термины и свойства интервалов
Тёмную краску как принято у музыкантов будем называть минорной а светлую — мажорной. Акцентируемый звук будем называть тоникой. Обозначать минорную будем буквой б(бета) а мажорную а(альфа). Эти краски противоположны друг другу. Увеличение мажорной равно уменьшению минорной и наоборот.
Почему в приведённой выше мелодии 2 напрашивался ход на 2 кварты вверх(G-C-F) — минорное движение вопреки общему мажорному? А для того чтобы сбросить накопившееся (мажорное) напряжение связанное с удалением от акцентируемого звука тоники. Сброс музыкального напряжения называется разрешением.
Получение обращения интервала путём октавного переноса звука
Такие тесно связанные интервалы называют обращениями по отношению друг к другу. Квинта обращение кварты, кварта обращение квинты. Обращение это и процедура переноса на октаву звука всякого интервала как сказано выше. Повторяя эту процедуру можно получить бесконечное количество обращений. Но за основной вид интервала будем принимать самое компактное обращение, а остальные представлять его обращениями.
Общее в обращениях — одинаковая плавность приращения мажорности или минорности. Различное — движение в одном направлении на обращение интервала, даёт приращение противоположной интервалу краски. То есть квинта вверх — мажорна, её обращение кварта вверх — минорна.
Интервалы, дающие мажорное приращение при ходе вверх будем называть интервалами квинтового строения(или большими). Интервалы, дающие минорное, противоречивые 3 — квартового(или малыми). Это универсальные свойства всех интервалов. О главном из них поговорим в конце статьи.
Мы можем откладывать квинты от звука(F на рисунке ниже) как вверх так вниз сколь угодно, формируя бесконечную квинтовую цепь. Но в один момент, откладывая в обе стороны на шестой квинте мы наткнёмся на с виду одинаковые звуки, но значат они совсем разное — один очень минорный другой мажорный, но акустически, по высоте(октавы сокращаем) звучат одинаково. Это явление называют энгармонизм. Как слух воспримет звук на этой высоте зависит от контекста(подробно об этом в следующей статье).
Энгармонические звуки Cb-B находятся друг от друга на расстоянии 12 квинтовых шагов
Попробуем прыжки через 1 кварту[1:40]. Так мы быстрее приходим к далекому минорному звуку. Через квинту[1:48]. То же самое но к мажорному. Дадим название звукам в соответствии с их напряженностью и окраской. Напряженность растёт с каждым квинтовым шагом поэтому обозначим её соответствующим им числом. Краску обозначаем также а — мажорная, б — минорная. Как выяснили выше у звуков находящихся по квинтам вверх от тоники будет мажорная краска, у звуков по квинтам вниз — минорная.
Теперь вернёмся к прыжку через 1 квинту(рисунок ниже). Перенесем C по октавам к стартовому звуку Bb и увидим что эти звуки довольно близки. Этот новый интервал называется большая секунда. Он квинтового строения так как вверх ведет в более мажорный звук, причём в 2 раза более интенсивный(2a) чем если бы мы пошли на квинту(1a). Всё из-за содержания 2ух квинтовых шагов. Его обращение — малая септима квартового строения — ведет вверх в более минорный звук.
Большая секунда возникает как два шага по квинтовой цепи
Подобным образом продолжим квинтовую цепь и перенесём звуки по октавам ближе к тонике. Получим ещё 4 интервала:
Интервалы в развёрнутом(верхняя половина) и свёрнутом виде(нижняя)
Всего на данный момент имеем 6 интервалов(октаву не беру):
Большая секунда / Малая септима
Большая секста / Малая терция
Большая терция / Малая секста
Большая септима / Малая секунда
Увеличенная кварта / Уменьшенная квинта(тритон)
Статья создана на основе первого видео с моего канала «Природа звука». Для тех кто хочет лучше разобраться в теории рекомендую к просмотру.
Простейший способ создания музыкальной гармонии. Квинтовый круг с числами мажорности аккордов

В конце статьи будет инструкция как изготовить такой вращающийся круг

Если у вас нет доступа к инструменту и воспроизведению этих аккордов можете посмотреть видео в конце статьи. Там и аккорды и текст с озвучкой.
Можно перескочить через несколько и плавно вернуться назад. Получим фигуру «Пила»:

Следующее движение через один мельчайший шаг. Его называют кварто-квинтовым, так как звуки аккорда идут на квинту или кварту. Изменение между числами(далее дельта Δ) 3. В этих ходах уже больше динамики(напряженности), чем в предыдущих:

Первое что важно в аккордовых прогрессиях так это периодическое возвращение к тоническому аккорду. Без этого слух просто потеряет ориентир и не сможет дальше интерпретировать аккорды.
На ощущение завершенности прогрессии аккордов заметно влияет метрическое положение аккордов.
Наиболее завершённо звучит тонический аккорд на сильном времени метра(такте), иначе будет запущена фаза движения, подстёгивающая гармонию к развитию. В простом чередовании Cm Gm Cm Gm в размере 4/4 третий аккорд хоть и тонический но выпадает на метрическую фазу движения — относительно сильную долю квадрата поэтому не звучит завершённо.
В этом движении уже наблюдаем некую закономерность о которой сейчас поговорим:

Секрет золотой секвенции
Рассмотрим золотую секвенцию(тонику поменяли на A):
Am Dm G C F Bdim Em Am
Im-IVm-VIIb-IIIb-VIb-IIdim-Vm-Im
Путь аккордов золотой секвенции на квинтовом круге можно представить так:



Из-за ограничения 7звучного лада, в ходе Dm-G нижний звук F, что далее должен быть Bb переносится на 6 квинт вверх в звук B. То же самое и дальше при ходе F-Bdim и Bdim-Em.
В итоге мы видим, что золотая секвенции это движение звуков по нисходящему ладу Шепарда, создающее иллюзию постоянного минорного движения вниз по квинтовой цепи.
Все разновидности ладов Шепарда звучат гармонично, поэтому ниже покажу все что нашёл
Секвенцию можно перевернуть, брать из неё фрагменты и смещать начало(звучать всегда будет хорошо). Например прогрессия Am Em Bdim F это первые 4 аккорда перевёрнутой. Если начать секвенцию с аккорда C то получим круговую цепочку в мажоре: C F Bdim Em Am Dm G C. Вот пример использования крупного фрагмента перевернутой: Am C G Dm Am Em Bdim F.
Динамичная золотая секвенция
На рисунке выше лад Шепарда с шагом 2 или динамичная золотая секвенция(тоника С). Все звуки идут на 2 шага вниз по квинтовой цепи, а вверх переносятся если выходят за пределы лада. Самая динамичная её часть(Bb-Ab-Gm) подчёркнута красным, остальные ходы(Fm-Eb-Ddim-Cm-Bb) очень спокойны(Δ+1).
Осевые прогрессии
Особенность большинства прогрессий с формой волны в том, что крайние звуки на цепи очерчивающие большую терцию движутся равномерно на квинту вверх и вниз вокруг виртуальной оси(красная линия). Их назовём осевыми. Принцип сохранится если любой аккорд этой последовательности заменить на ему параллельный(на квинтовом круге) с общей большой терцией. Осевую можно логически продолжить по принципу золотой, получим часть восходящего лада Шепарда:
Вернёмся к простым аккордам.
Перед минорной тоникой на крайней мажорной точке движения вместо аккорда VIIb(Bb) lin-1 или Vm(Gm) lin1 часто встречается мажорная доминанта со значением 8(G подчеркнул на рисунке ниже) для усиления мажорности на этой фазе движения гармонии и более резкого утвердительного прихода в тонику(8->-2 Δ10). Возникает один внеладовый звук VII(B), а квинта(G-D) остается в ладу. При этом в цепочке также могут присутствовать аккорды Bb или Gm например в фигуре шаг вперед 2 назад или обратной осевой гармонической :
Динамичные прогрессии с участием мажорной доминанты
Круг с квартаккордами(sus), уменьшенными и увеличенными.
Круг аккордов С
А сейчас анализ гармонии на примере простой популярной песни Hi-Fi «Седьмой лепесток»(тоника Bb).
Анализ гармонии
Припев плавно(Δ-3) выходит на тонический аккорд проигрыша. Далее в проигрыше идёт простая волна кварто-квинтовыми шагами:
Весь гармонический путь песни:

Как мы увидели, для запуска гармонии достаточно создать логичное движение звуков по квинтовой цепи(квинтовый подход, например как в золотой секвенции) или логичное движение значений аккордов(линейный подход, гармонические фигуры ).
Изготавливаем вращающийся круг аккордов со значениями мажорности
После всех действий установите нужную тонику в верхнее положение как вначале статьи на рисунке «Установка тоники».
Квинтовые круги аккордов(файлы «Круг для печати» и «Круг для печати sus,dim,aug») и программу музыкальный анализатор для просмотра аккордов на квинтовой цепи(видеоинструкция на канале) можно скачать здесь.
Статья создана на основе видео с моего канала «Природа звука». Для тех кто хочет закрепить прочитанное и лучше разобраться в теории рекомендую к просмотру: