Начальное положение точки 3 0 чему равен модуль вектора
|r| = √ 3 ^ 2 + 4 ^ 2 = √ 25 = 5
Тело переместилось в точку с координатами х = 2 и у = 1мю Найдите проекция вектора перемещениях на осях х и у.
Найдите координаты координаты конечного положения тела.
Чему равен его модуль?
Помогите пожалуйста?
Найдите координаты координаты конечного положения тела.
Чему равен его модуль?
Решите пожалуйста задачи?
Решите пожалуйста задачи.
Определите, на какой высоте находится муха.
Модуль вектора гА равен 5 м.
Определите модуль вектора гв и угол, который он составляет с осью ОХ.
Модули векторов равны 3 и 5, 2 м.
Определите модуль полученного вектора и угол, который он составляет с осью OX.
Как определяют положение точки в пространстве?
Как определяют положение точки в пространстве?
Опишите характер движения точки, найдите начальную координату, модуль и направление вектора скорости.
Чему равно ускорение материальной точки?
Какими величинами определяется положение точки на плоскости?
Какими величинами определяется положение точки на плоскости?
Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5?
Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5.
Найдите координаты конечного полодения тела.
Начертите вектор перемещения.
Чему равен его модуль?
Как задают положение точки в пространстве с помощью координат?
Как задают положение точки в пространстве с помощью координат.
|r| = √ 3 ^ 2 + 4 ^ 2 = √ 25 = 5
Тело переместилось в точку с координатами х = 2 и у = 1мю Найдите проекция вектора перемещениях на осях х и у.
Найдите координаты координаты конечного положения тела.
Чему равен его модуль?
Помогите пожалуйста?
Найдите координаты координаты конечного положения тела.
Чему равен его модуль?
Решите пожалуйста задачи?
Решите пожалуйста задачи.
Определите, на какой высоте находится муха.
Модуль вектора гА равен 5 м.
Определите модуль вектора гв и угол, который он составляет с осью ОХ.
Модули векторов равны 3 и 5, 2 м.
Определите модуль полученного вектора и угол, который он составляет с осью OX.
Как определяют положение точки в пространстве?
Как определяют положение точки в пространстве?
Опишите характер движения точки, найдите начальную координату, модуль и направление вектора скорости.
Чему равно ускорение материальной точки?
Какими величинами определяется положение точки на плоскости?
Какими величинами определяется положение точки на плоскости?
Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5?
Помогитеиз начальной точки с координатами х0 = 3м и у0 = 1м тело прошло некоторый путь, так что проекция вектора перемещения на ось х оказалась равной 5.
Найдите координаты конечного полодения тела.
Начертите вектор перемещения.
Чему равен его модуль?
Как задают положение точки в пространстве с помощью координат?
Как задают положение точки в пространстве с помощью координат.
r (3;0) ;
x = 3
y = 4
|r| = √ 3^2 +4^2 = √ 25 =5
Другие вопросы из категории
друг от друга на расстояние 15 см так, что нити образовали прямой угол. Чему равен заряд каждого шарик? Ответ округлить с точностью до десятых долей микрокулона.
Ответ должен быть числом, без всяких степеней.
и площадью поперечного сечения 0,1 мм^2
Читайте также
2. Уравнение зависимости координаты прямолинейного движущегося тела время от времени имеет вид: x=2-3t+4t^2. Чему равен модуль ускорения тела?
3. Как должен двигаться самолет, чтобы пилот испытывал состояние невесомости?
а) равномерно и прямолинейно
б) по окружности с постоянной по модулю скоростью
в) с ускорением g
г) с любым ускорением
песчинки равна 10–6 кг. Чему равен модуль вектора напряженности электрического поля? Ответ выразите в кВ/м.
перпендикулярен линиям индукции однородного магнитного поля. Чему равен
модуль индукции магнитного поля, если при токе2 А на проводник действует
сила, модуль которой равен 0,01 H?»
250 Н2.
Как движется материальная точка при равенстве нулю суммы всех действующих на нее сил? Какое утверждение верно? 1) скорость материальной точки обязательно равна нулю 2) скорость материальной точки возрастает со временем 3) скорость материальной точки постоянна и обязательно не равна нулю 4) скорость материальной точки может быть любой, но обязательно постоянной во времени
Метеорит пролетает около Земли за пределами атмосферы. Как направлен вектор ускорения метеорита в тот момент, когда вектор силы гравитационного притяжения Земли перпендикулярен вектору скорости метеорита?
1) параллельно вектору скорости 2) по направлению вектора силы 3) по направлению вектора скорости 4) по направлению суммы векторов силы и скорости
Чему равен модуль равнодействующей этих сил?
§ 2. Способы описания движения
Вспомните из курса физики основной школы физические величины, которыми можно описать механическое движение тела.
Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчёта.
Существует несколько способов описания, или, что одно и то же, задания движения точки. Рассмотрим два из них, которые наиболее часто применяются.
Координатный способ. Будем задавать положение точки с помощью координат (рис. 1.3). Если точка движется, то её координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.
Математически это принято записывать в виде

Запомни
Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме.
Если уравнения движения известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и её положение относительно выбранного тела отсчёта. Вид уравнений (1.1) для каждого конкретного движения будет вполне определённым.
Важно
Основной задачей кинематики является определение уравнении движения тел.
Количество выбираемых для описания движения координат зависит от условий задачи. Если движение точки происходит вдоль прямой, то достаточно одной координаты и, следовательно, одного уравнения, например, x(t). Если движение происходит на плоскости, то его можно описать двумя уравнениями — x(t) и y(t). Уравнения (1.1) описывают движение точки в пространстве.
Векторный способ. Положение точки можно задать, и с помощью радиус-вектора.
Запомни
Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.
При движении материальной точки радиус-вектор, определяющий её положение, с течением времени изменяется (поворачивается и меняет длину; рис. 1.4), т. е. является функцией времени:
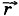
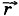
На рисунке 1.4 радиус-вектор 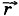
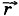
Запомни
Формула (1.2) есть уравнение движения точки, записанное в векторной форме.
Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.
Важно
Таким образом, задание трёх скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).
Итак, мы знаем, что положение точки в пространстве определяется её координатами или её радиус-вектором.
Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось?
Изобразим какую-либо ось (рис. 1.5), например ось ОХ. Опустим из начала А и конца В вектора 

Запомни
Проекцией вектора 

Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, ах и ау — проекции вектора 
Согласно определению проекции вектора на ось можно записать:
Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора.
Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций (рис. 1.6). В противном случае (см. рис. 1.5) она считается отрицательной.
Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол φ с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекции тупой угол φ.







Ключевые слова для поиска информации по теме параграфа.
Уравнения движения. Радиус-вектор. Проекция вектора.
Вопросы к параграфу
1. Какими способами можно задать положение точки?
2. Как задают положение точки в пространстве с помощью координат?
3. Что называется радиус-вектором?
4. Что называется проекцией вектора на ось?
5. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции?
6. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции?
7. Чему равна проекция вектора на перпендикулярную к нему ось?











