Напряжение в металле в чем измеряется

Напряжение в металле в чем измеряется

Электрическим током (I) называется направленное движение электрических зарядов (ионов — в электролитах, электронов проводимости в металлах).
Необходимым условием для протекания электрического тока является замкнутость электрической цепи.

Электрический ток измеряется в амперах (А).

Производными единицами измерения тока являются:
1 килоампер (кА) = 1000 А;
1 миллиампер (мА) 0,001 А;
1 микроампер (мкА) = 0,000001 А.

Человек начинает ощущать проходящий через его тело ток в 0,005 А. Ток больше 0,05 А опасен для жизни человека.

Электрическим напряжением (U) называется разность потенциалов между двумя точками электрического поля.

Единицей разности электрических потенциалов является вольт (В).
1 В = (1 Вт) : (1 А).

Производными единицами измерения напряжения являются:

1 киловольт (кВ) = 1000 В;
1 милливольт (мВ) = 0,001 В;
1 микровольт (мкВ) = 0,00000 1 В.

Сопротивлением участка электрической цепи называется величина, зависящая от материала проводника, его длины и поперечного сечения.

Электрическое сопротивление измеряется в омах (Ом).
1 Ом = (1 В) : (1 А).

Производными единицами измерения сопротивления являются:

1 килоОм (кОм) = 1000 Ом;
1 мегаОм (МОм) = 1 000 000 Ом;
1 миллиОм (мОм) = 0,001 Ом;
1 микроОм (мкОм) = 0,00000 1 Ом.

Электрическое сопротивление тела человека в зависимости от ряда условий колеблется от 2000 до 10 000 Ом.

Удельным электрическим сопротивлением (ρ) называется сопротивление проволоки длиной 1 м и сечением 1 мм2 при температуре 20 °С.

Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью (γ).

Мощностью (Р) называется величина, характеризующая скорость, с которой происходит преобразование энергии, или скорость, с которой совершается работа.
Мощностью генератора называется величина, характеризующая скорость, с которой механическая или другая энергия преобразуется в генераторе в электрическую.
Мощностью потребителя называется величина, характеризующая скорость, с которой происходит преобразование электрической энергии в отдельных участках цепи в другие полезные виды энергии.

Системной единицей мощности в СИ является ватт (Вт). Он равен мощности, при которой за 1 секунду выполняется работа в 1 джоуль:

Производными единицами измерения электрической мощности являются:

1 киловатт (кВт) = 1000 Вт;
1 мегаватт (МВт) = 1000 кВт = 1 000 000 Вт;
1 милливатт (мВт) = 0,001 Вт; о1i
1 лошадиная сила (л. с.) = 736 Вт = 0,736 кВт.

Единицами измерения электрической энергии являются:

1 ватт-секунда (Вт сек) = 1 Дж = (1 Н) (1 м);
1 киловатт-час (кВт ч) = 3,б 106 Вт сек.

Пример. Ток, потребляемый электродвигателем, присоединенным к сети 220 В, составлял 10 А в течение 15 минут. Определить энергию, потребленную двигателем.
Вт*сек, или, разделив эту величину на 1000 и 3600, получим энергию в киловатт-часах:

W = 1980000/(1000*3600) = 0,55кВт*ч

Рассмотрим основные электрические величины, которые мы изучаем сначала в школе, затем в средних и высших учебных заведениях. Все данные для удобства сведем в небольшую таблицу. После таблицы будут приведены определения отдельных величин, на случай возникновения каких-либо непониманий.

Таблица физических величин и их описание:

Существуют десятичные приставки, которые используются в названии величины и служат для упрощения описания. Самые распространенные из них: мега, мили, кило, нано, пико. В таблице приведены и остальные приставки, кроме названных.

Сила тока в 1А – это величина, равная отношению заряда в 1 Кл, прошедшего за 1с времени через поверхность (проводник), к времени прохождения заряда через поверхность. Для протекания тока необходимо, чтобы цепь была замкнутой.

Сила тока измеряется в амперах. 1А=1Кл/1c

В практике встречаются

Электрическое напряжение – разность потенциалов между двумя точками электрического поля. Величина электрического потенциала измеряется в вольтах, следовательно, и напряжение измеряется в вольтах (В).

1Вольт – напряжение, которое необходимо для выделения в проводнике энергии в 1Ватт при протекании по нему тока силой в 1Ампер.

В практике встречаются

Электрическое сопротивление – характеристика проводника препятствовать протеканию по нему электрического тока. Определяется как отношение напряжения на концах проводника к силе тока в нем. Измеряется в омах (Ом). В некоторых пределах величина постоянная.

1Ом – сопротивление проводника при протекании по нему постоянного тока силой 1А и возникающем при этом на концах напряжении в 1В.

Из школьного курса физики все мы помним формулу для однородного проводника постоянного сечения:

R=ρlS – сопротивление такого проводника зависит от сечения S и длины l

где ρ – удельное сопротивление материала проводника, табличная величина.

Между тремя вышеописанными величинами существует закон Ома для цепи постоянного тока.

Ток в цепи прямо пропорционален величине напряжения в цепи и обратно пропорционален величине сопротивления цепи – закон Ома.

Электрической емкостью называется способность проводника накапливать электрический заряд.

Емкость измеряется в фарадах (1Ф).

1Ф – это емкость конденсатора между обкладками которого возникает напряжение 1В при заряде в 1Кл.

В практике встречаются

Индуктивность – это величина, характеризующая способность контура, по которому протекает электрический ток, создавать и накапливать магнитное поле.

Индуктивность измеряется в генри.

1Гн – величина, равная ЭДС самоиндукции, возникающей при изменении величины тока в контуре на 1А в течение 1секунды.

Источник

Закон Ома: как связаны между собой напряжение, ток и сопротивление

Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Единицы измерения: вольт, ампер и ом

Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:

Единицы измерения тока, напряжения, сопротивления

Величина	Символ	Единица измерения	Сокращение единицы измерения
Ток	I	Ампер	А
Напряжение	V	Вольт	В
Сопротивление	R	Ом	Ом

«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.

Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.

Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.

Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.

Кулон и электрический заряд

Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.

Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.

Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.

Формула закона Ома

Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

Рисунок 1 – Пример простой схемы

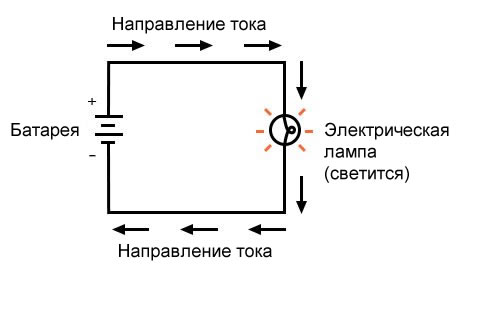
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

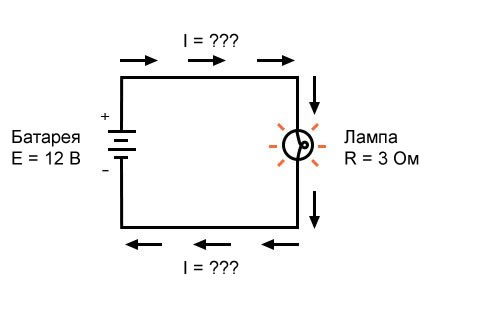
Какая величина тока (I) в этой цепи?

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

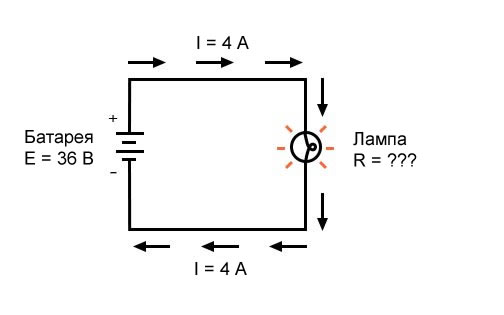
Какое сопротивление (R) оказывает лампа?

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

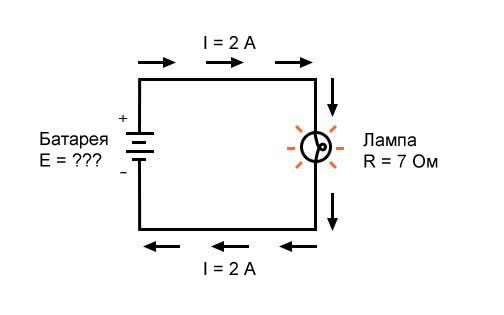
Какое напряжение обеспечивает батарея?

\[E = IR = (2 \ А)(7 \ Ом) = 14 \ В\]

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

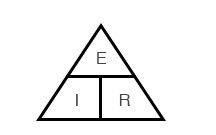
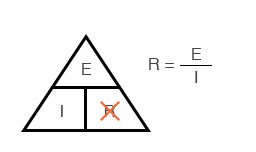
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

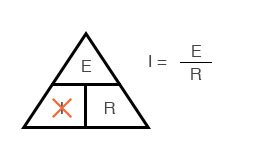
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

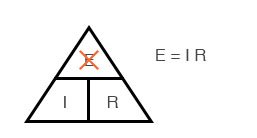
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Источник

Определение внутренних напряжений в металлах

ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ НАПРЯЖЕНИЙ

Учебно-методические указания к выполнению лабораторной работы

по курсу «Рентгеноструктурный анализ»

Министерство образования и науки РФ

Омский государственный университет

ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ НАПРЯЖЕНИЙ

Учебно-методические указания к выполнению лабораторной работы

по курсу «Рентгеноструктурный анализ»

Издание ОмГУ Омск 2004

Учебно-методические указания к выполнению лабораторной работы по курсу «Рентгеноструктурный анализ». Омск, 2004. 22с.

В работе даются методы рентгенографического определения внутренних напряжений в металлах на порошковом рентгеновском дифрактометре.

Работа утверждена в качестве учебно-методических указаний к выполнению лабораторной работы на Ученом Совете физического факультета 23 апреля 2004 г.

ã Омский госуниверситет, 2004

Цель работы: ознакомиться с методами рентгенографического определения внутренних напряжений в металлах; определить области когерентного рассеяния и микронапряжения в металлах, подвергнутых пластической деформации при облучении мощным ионным пучком.

Принадлежности: дифрактометр «ДРОН-3М», эталонный и деформированный образцы металлов (облученные мощным ионным пучком).

При приложении к металлическому образцу напряжения, превосходящего предел упругости, металл пластически деформируется. Это приводит к повышению предела упругости, изменяются и другие физические и физико-химические свойства металла. С увеличением степени пластической деформации повышается внутренняя энергия металла, искажается его кристаллическая структура, меняются свойства: металл упрочняется, понижается сопротивление коррозии, увеличивается скорость диффузии и фазовых превращений, понижается плотность, появляется анизотропия свойств, связанная с предпочтительной ориентацией кристаллитов (текстурой).

Типы внутренних напряжений

В основе классификации внутренних напряжений лежит отличие в объемах, в которых эти напряжения уравновешиваются /1-3/.

1. Под зональными (остаточными) напряжениями (макронапряжениями или напряжениями I-рода) понимают упругие искажения, уравновешивающиеся в объеме всего изделия или в его значительной части. При наличии макронапряжений удаление какой-либо части детали приводит к нарушению равновесия между остальными ее частями, что вызывает деформирование (коробление и растрескивание) изделия. Разрушение происходит большей частью под действием растягивающих напряжений. Сжимающие напряжения (их можно создавать специальными технологическими процессами) снижают чувствительность материала к концентраторам напряжений и повышают усталостную прочность материала.

2. Под микронапряжениями (II-рода) понимают напряжения, которые уравновешиваются в объеме отдельных кристаллитов или частей кристаллитов (мозаичных блоков). Они могут быть как неориентированными, так и ориентированными (в направлении усилия, произведшего пластическую деформацию).

3. Под статическими искажениями решетки (III-рода) понимают напряжения, которые уравновешиваются в пределах небольших групп атомов. В деформированных металлах статические искажения уравновешиваются в группах атомов, лежащих у границ зерен, плоскостей скольжения и т. д. Такие искажения могут быть связаны с дислокациями. Смещения атомов из идеальных положений (узлов решетки) могут также возникать в кристаллах твердого раствора из-за различия размеров атомов и химического взаимодействия между одноименными и разноименными атомами, образующими твердый раствор. При наличии микронапряжений и статических искажений удаление части тела не приводит к их перераспределению.

Напряжения разных типов приводит к различным изменениям рентгенограмм и дифрактограмм, что позволяет изучать внутренние напряжения рентгенографическими методами. Макронапряжения вызывают сдвиг интерференционных линий, который становится особенно заметным под большими брэгговскими углами. Микронапряжения и измельчение блоков мозаики (области когерентного рассеяния) приводят к уширению линий. Наибольшее изменение ширины интерференционных линий наблюдают при больших брэгговских углах. Ориентированные микронапряжения могут также вызывать смещение линий. При наличии статических искажений, связанных со смещением атомов из идеальных положений, уменьшается интенсивность интерференционных линий и возрастает диффузный фон. Эффект уменьшения интенсивности особенно заметен для линий с большими индексами.

Определение зональных напряжений (макронапряжений)

Макронапряжения возникают при неоднородном нагреве или охлаждении (например, при сварке, огневой резке), в процессе холодной прокатки или правки готовых изделий, в результате структурных превращений, при химической и механической обработке поверхности (точении, шлифовке, полировке), а также при нанесении электролитических покрытий. Контроль макронапряжений имеет важное значение в практике, так как позволяет значительно повышать надежность изделий в эксплуатации.

Основой рентгеноструктурного метода определения зональных ис­кажений является то, что все атомные плоскости во всех кристаллитах поликристалла, одинаково ориентированные по отношению к действу­ющим упругим силам, однородно меняют свои межплоскостные рассто­яния (для них =const ).

Напряжения на поверхности образца (рис. 1) можно разложить на главные (s1, s2 и s3), которые являются нормальными и тангенциаль­ными (к поверхности образца).

Рис. 1. Угловые соотношения между главными напряжениями s1; s2; s3, измеряемым напряжением sj и координатными осями х, у, z

Нормальная составляющая напряже­ния s3 нa поверхности равна нулю. Строго говоря, s3=0 только при плосконапряженном состоянии, но в большинстве случаев величиной s3 можно пренебречь.

Упругая деформация в поверхностных слоях образца в направлении, перпендикулярном поверхности образца, будет

, (1)

m — коэффициент Пуассона.

(2)

Определение может быть произведено съемкой рентгено­грамм с поверхности ненапряженного и напряженного образцов. При этом должны быть соблюдены следующие условия:

1. Излучение и отражающие плоскости должны быть подобраны так, чтобы угол отражения был максимально близок к 83-85° (прак­тически он равен 75-85°).

Рекомендуемые излучения для разных металлов и сплавов даны в таблицах приложения /2/.

2. Линии рентгенограммы должны быть острыми и четкими. Для этого следует пользоваться малыми диафрагмами и хорошо подготав­ливать поверхность образцов.

Ошибка в нахождении d = ± 0,0001 кХ может привести при съемке стальных образцов к ошибке в определении s1 + s2 = 1,7 кг/мм2.

Более сложной является задача определения величины напряже­ния, действующего на поверхности в данном конкретном направлении (напряжение sj, см. рис. 1).

1. При определении суммы главных напряжений используют соотношение:

где d0- межплоскостное расстояние для ненапряженного материала,

d^- среднее межплоскостное расстояние для напряженного материала в направлении, перпендикулярном к поверхности образца.

2. Измерение составляющей напряжения в заданном направлении методом двух съемок проводят по соотношению:

3. Для увеличения точности измерения напряжений I-рода применяют метод пяти наклонных съемок с y=0; ±30 и ± 450. Расчет проводится путем экстраполяции по соотношению:

4. Раздельное определение главных напряжений проводится путем съемки трех рентгенограмм: одной с напряженного образца под постоянным углом y к нормали и двух с ненапряженного при наклонах плоскости образца j и j+ 900. Расчет проводится по формулам:

L = (dy-dy¢ ) /d0 [ E/ (1+m) sin2y];

5. При неизвестных величинах и направлениях главных напряжений в поверхностном слое проводит съемку под углами j, j+600 и j-600. Расчет напряжений проводят по соотношениям:

где М=sj+sj+60 +sj-60s; N = Ö(3sj-M)2+3[sj-60-sj+60]2.

Микронапряжения могут возникать:

1. При пластической деформации поликристаллического образца из-за упругой и пластической анизотропии кристаллов;

3. В процессе распада пересыщенного твердого раствора (старения) (на границах областей выделившейся фазы и матрицы создаются микронапряжения, связанные с сопряжением решеток).

4. При локальных структурных или химических превращениях (изменение удельного объема какого-то слоя по отношению к основной массе также приводит к появлению микронапряжений).

Область когерентного рассеяния (ОКР) – это минимальный размер частицы вещества, имеющей правильное кристаллическое строение, на которой рентгеновские лучи рассеиваются когерентно, то есть с постоянной разностью фаз. Частицы и области когерентного рассеяния размером меньшим 1×10-5 см ¸1,5×10-5 см вызывают эффект размытия линий на рентгенограмме. Рентгенографические методы определения дисперсности (размеров ОКР) также основаны на анализе ширины дифракционных линий /3-6/. Известно /1, 3/, что ширина максимумов интерференционной функции Лауэ в обратном пространстве (то есть ширина пиков на дифрактограмме) обратно пропорциональна количеству рассеивающих центров (атомов, плоскостей) вдоль данного направления. Ширина дифракционного максимума определяется на половине его высоты, или интегральная ширина «В» определяется по формуле:

,

Нужно иметь в виду, что ширина каждой экспериментальной линии В состоит из двух частей: инструментальной ширины b (ширина линии эталона), зависящей от геометрии съёмки, расходимости пучка, размера фокуса трубки и т. д., и физического уширения b, определяемого факторами несовершенства структуры (дисперсностью, микроискажениями, дефектами упаковки и т. д.). Эти величины не просто арифметически складываются, а каждый элемент инструментальной линии испытывает физическое уширение, что можно выразить уравнением типа свертки:

Рис. 2. Схема формирования уширенной дифракционной линии.

В зависимости от вида функций, описывающих эти кривые, будет по-разному выражаться и связь между ширинами линий В, b и b, из которых первые две величины определяются экспериментально. А физическое уширение определяют из формул, связывающих эти три величины, и b зависит от способа описания профилей дифракционных линий на экспериментальной и инструментальной кривой интенсивности.

При экспрессном определении физического уширения пользуются аппроксимирующими функциями, которые хорошо себя зарекомендовали во многих работах, такими как функции Гаусса, Коши, Лорентца и др., которые часто используют для описания профилей различных спектральных линий. Так, если экспериментальная кривая h(х) и эталонная f(x) описываются

соответственно функциями Коши f(x) =; g(x)= , то в этом случае физическое уширение будет равно b=В-b.

Если f(x)= , g(y)= , то в этом случае физическое

уширение .

Пригодность той или иной аппроксимирующей функции можно проверить, если построить график I(х) в координатах, спрямляющих аппроксимирующие функции. Например, функция Гаусса у= изобразится прямой в координатах lny=f(x2) и т. д. Но более точным способом является подбор аппроксимирующих функций по соответствующим программам. Например, для описания профиля дифракционных линий может быть выбрана функция Пирсона, профильные параметры которой подбираются уточнением методом наименьших квадратов до наилучшего соответствия с экспериментальной кривой, что оценивается фактором расходимости R. Функция Пирсона замечательна тем, что она включает в себя, как частные случаи, эмпирически найденные функции для описания профилей дифракционных линий по Коши, Гауссу или Лорентцу. Методом, не требующим произвольного выбора аппроксимирующих функций и основанном на анализе формы экспериментально измеренных линий, является метод гармонического анализа /1,3/, который достаточно трудоемок и не может быть отнесен к простым.

Найденное таким образом физическое уширение b может быть использовано для определения размеров ОКР в направлении, перпендикулярном отражающей плоскости с индексами hkl:

Рис.4. График поправок на геометрическое уширение линий в зависимости от

Если из условий эксперимента можно заведомо вывести заключение о том, что истинное физическое уширение линии (hkl) вызвано или исключительно микронапряжениями, или только измельчением кристаллитов, то величина искажений решетки так же, как и размер кристаллита в направлении, нормальном к плоскости (hkl), могут быть вычислены по простым формулам:

-для средней величины микроискажений = b/4tgqhkl (4)

-для средней величины ОКР по формуле Dhkl= . (5)

Зная истинные физические уширения b1 и b2 двух порядков отражения от одной и той же системы плоскостей (hkl), можно провести качественную оценку доли влияния факторов размера частиц и микронапряжений. Если уширение вызвано только микроискажениями, то из формулы (4) следует, что:

,

т. е. уширение пропорционально tgq. Если в образце нет искажений и всё уширение вызвано только мелким размером частиц, то тогда из формулы (5) следует, что:

,

т. e. уширение обратно пропорционально cos q. Если же уширение вызвано обоими этими факторами, то отношение истинных физических уширений находится между отношением косинусов и тангенсов

. (6)

В этом случае для разделения эффектов дисперсности и микроискажений нужно воспользоваться двумя порядками отражения от одной системы плоскостей и воспользоваться различной зависимостью дисперсности и микроискажений от sinq/l. Например, если считать, что уширение за счет дисперсности и за счет микроискажений описывается функцией Коши, то можно построить зависимость для разных порядков отражения в виде:

bcosq =l/D + 4(Dd/d)×sinq (7).

Это есть уравнение прямой, где отрезок, отсекаемый по оси ординат, даст величину l/D, откуда находим размер ОКР, а из наклона прямой определяем Dd/d.

Если обе функции имеют вид , то можно построить аналогичную зависимость для двух порядков отражения в виде:

(bcosq )2= (l /D )2+ (4sinq)2 (8).

Таким образом, если для исследуемого объекта аппроксимирующие функции известны, то истинное физическое уширение определяют следующим образом. Снимают рентгенограмму для исследуемого объекта и эталона в одинаковых условиях. В качестве эталона для нахождения инструментального уширения используют образец, с заведомо крупными ОКР (

Å) и без нарушений кристаллического строения. Определив площади под дифракционными кривыми интенсивности и их высоты и поделив площади на соответствующие высоты, получают экспериментальные общие уширения линий рабочего образца В и эталона b. Уширения выражают в долях градусов 2q и в радианах. Затем, если требуется, вводится поправка на немонохроматичность излучения для ширины линий рабочего образца и эталона, и находится значение истинного физического уширения. Далее, по формуле (6) нужно проанализировать, чем обусловлено уширение линий (дисперсностью или микроискажениями) и либо по формуле Шеррера-Селякова находят размер ОКР в определенном направлении [hkl], либо из уравнения (7) или (8) находят размер ОКР и величину микроискажений.

Нужно учитывать, что полученные аппроксимационным методом абсолютные величины ОКР могут быть определены с точностью до аппроксимационной функции, то есть зависят от вида аппроксимирующей функции и могут различаться в 1.5-2 раза. Относительные измерения ОКР в зависимости от какого-либо фактора и измеренные одинаковым способом могут быть оценены достаточно точно с погрешностью не более 5-10% от определяемых величин. Более точные данные о размерах ОКР, об их распределении по размерам и о микроискажениях могут быть получены методом гармонического анализа дифракционных линий или при уточнении реальной структуры по полному профилю рентгенограммы. Сравнительная характеристика размеров ОКР почти всегда сопровождает изучение фазового состава, так как дает информацию о причинах изменения поверхности в результате термических превращений или воздействий реакционной среды.

Определение статических искажений (III – рода)

Статические искажения связаны с отклонением атомов из положений равновесия, определяемых узлами решетки. Эти искажения охватывают группы, участвующих в создании нарушений структуры. Статические напряжения возникают при наличии в кристаллах различного рода дефектов (дислокаций, атомов внедрения, вакансий). Статические искажения могут также возникать в твердых растворах типа замещения при различии атомных радиусов растворяемого металла и металла-растворителя. Статические искажения, вызванные смещением атомов из их нормальных положений, должны давать такой же эффект, как и смещение атомов при тепловых колебаниях (последние называют динамическими искажениями). Ослабление интерференционных линий вследствие тепловых колебаний характеризуется температурным множителем:

где, для кубической решетки: М = (8/3)p2U2д(sinq/l)2;

где Uд2- среднее квадратичное смещение атомов при статических искажениях.

Статические искажения не могут существовать в чистом виде, без динамических искажений, поэтому на интенсивность линий рентгенограммы влияют оба фактора. По уменьшению интенсивности можно оценить величину искажения.

Простейшим способом оценки искажений является измерение отношения интенсивностей линии и фона на рентгенограммах образцов с искаженной и неискаженной решетками. Уменьшение соотношения Ihkl/Iфон соответствует увеличению искажений решетки.

Другим методом оценки искажений является измерение отношений интенсивностей двух линий на рентгенограмме одного и того же образца в деформированном и недеформированном состоянии или линий образца и эталона. Величина смещения атомов из равновесного положения в решетке может быть вычислена по соотношению:

U2ст= 3а2ln[(I1/I2)деф/(I1/I2)недеф]/4p2[(h22+k22+lh12+k12+l2)]. (9)

При необходимости более точного измерения проводят разделение влияния статической и динамической составляющих смещений атомов. При этом измеряют отношение интенсивностей одних и тех же линий на рентгенограммах образцов с неискаженной решеткой, где смещения атомов обусловлены только динамическими (тепловыми) искажениями, и образцов с кристаллической решеткой искаженной вследствие образования твердого раствора, пластической деформации и т. д., где смещения атомов связаны как с динамическими, так и с устойчивыми статическими искажениями.

1. С помощью преподавателя получить дифрактограмму от кристаллов недеформированного и деформированного (облученного мощным ионным пучком).

2. По полученным дифрактограммам рассчитать по формуле Вульфа-Брэгга межплоскостные расстояния и оценить по формуле (2) напряжения I-рода (значения Е и m для исследуемых материалов взять у преподавателя).

3. Рассчитать размер ОКР и величину микроискажений, предварительно проанализировав по формуле (6) чем обусловлено уширение линий (дисперсностью или микроискажениями). Результаты анализа позволять выбрать необходимую формулу для расчета ОКР и e.

4. Оценить статические искажения двумя способами:

а) измеряя отношение Ihkl/Iфона ;

б) измеряя Iдеф. и Iнедеф.- для одних и тех же линий.

5. Рассчитать по формуле (9) величину среднеквадратичных смещений.

6. Оценить погрешность полученных результатов.

2. К каким изменениям на рентгенограмме приводят напряжения разных типов?

3. Как рентгенографически определяют напряжения I-рода?

4. Что называется областью когерентного рассеяния?

5. Что лежит в основе методов определения микронапряжений и ОКР?

6. С чем связаны статические искажения кристаллической решетки?

7. Как можно оценить напряжения III-рода?

3. Русаков металлов. Учебник для вузов. М.: Атомиздат, 19с.

6. Миркин контроль машиностроительных материалов. Справочник. М.: Изд-во МГУ, 19с.

7. Миркин по рентгеноструктурному анализу поликристаллов. М.: Физматгиз, 19с.

ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ НАПРЯЖЕНИЙ

Учебно-методические указания к выполнению лабораторной работы

по курсу «Рентгеноструктурный анализ»

Подписано в печать Формат бумаги 60´84 1/16

Источник