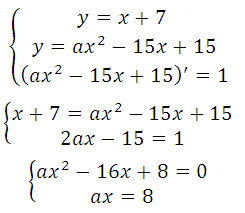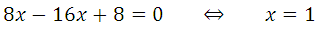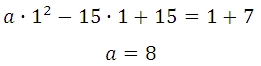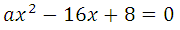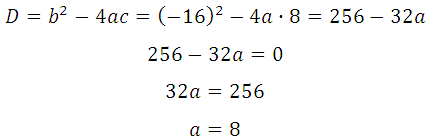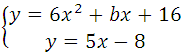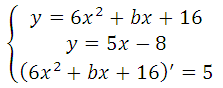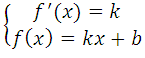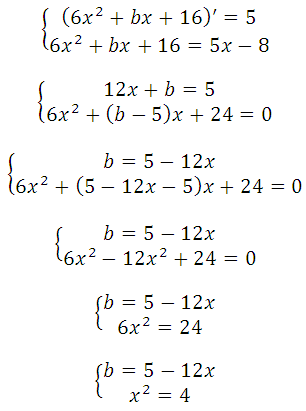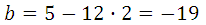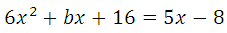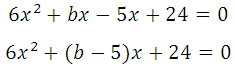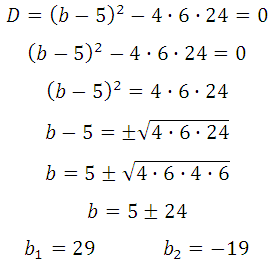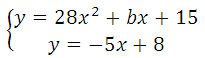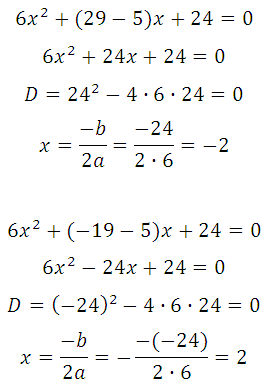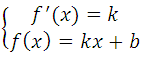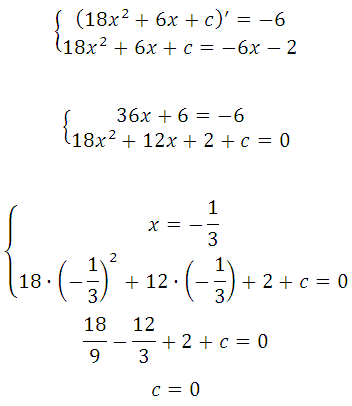Найдите положительный угловой коэффициент прямой если известно что она касается параболы

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

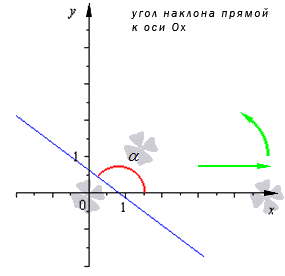
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Уравнение с угловым коэффициентом

Ответ: М 1 принадлежит прямой, а М 2 нет.

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Решение

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

Решим задачу обратную данной.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке

Эта математическая программа находит уравнение касательной к графику функции \( f(x) \) в заданной пользователем точке \( x_0 \).

Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).

Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.

Немного теории.

Угловой коэффициент прямой

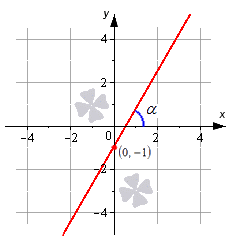
Уравнение касательной к графику функции

Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.

Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.

Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:

Нами получено уравнение касательной к графику функции \( y = f(x) \) в точке \( x=a \).

Алгоритм нахождения уравнения касательной к графику функции \( y=f(x) \)
1. Обозначить абсциссу точки касания буквой \( a \)
2. Вычислить \( f(a) \)
3. Найти \(f'(x) \) и вычислить \(f'(a) \)
4. Подставить найденные числа \( a, f(a), f'(a) \) в формулу \( y=f(a)+ f'(a)(x-a) \)

Источник

Общая касательная к графикам функций. На примере 2х парабол

На примере двух парабол покажем, как составить уравнение общей касательной к графикам функций. Заметим, что общих касательных может быть несколько.

Для решения данной задачи потребуются знания о производной на уровне школьного курса.

В рамках подготовки к профильному ЕГЭ при изучении производной я предлагаю своим ученикам решать, в том числе, и подобные задачи, помимо стандартных 7 и 12 заданий.

Это необходимо для того, чтобы школьники учились применять свои знания при решении задач, а не просто решать стандартные задания по шаблону.

Составим уравнение общих касательных к графикам квадратичных функций (параболам):

Касательная представляет собой прямую. Запишем уравнение касательной в виде уравнения прямой с угловым коэффициентом:
y = kx + b, k – угловой коэффициент.
Обозначим точку, в которой она касается первой параболы, как A (a1, a2), второй параболы – B (b1, b2).

Рассмотрим функцию

1. Вычислим ее производную: y’ = 2(x – 1).

Таким образом, мы выразили координаты точки A через угловой коэффициент касательной:
A (k/2 + 1, k^2/4 + 1).

3. Угловой коэффициент прямой, проходящей через точки A (a1, a2) и B (b1, b2), равен (a2 – b2) / (a1 – b1). Значит
k = (a2 – b2) / (a1 – b1).

Подставим в это уравнение координаты точек A и B и получим уравнение относительно k:

Находим корни: k = 0 и k = 4.

5. Составляем уравнение касательной (прямой) по двум точкам. (Данная тема разобрана в предыдущем посте)
(x – a1) / (b1 – a1) = (y – a2) / (b2 – a2)
(x – 3) / (1 – 3) = (y – 5) / (-3 – 5)
(x – 3) / (–2) = (y – 5) / (-8) – каноническое уравнение прямой
Выражаем y:
y = 4x – 7 – уравнение прямой с угловым коэффициентом.

Аналогично находим уравнение еще одной касательной (при k = 0):
y = 1.

✔ Для того, чтобы задать вопрос или записаться на консультацию, пишите в whatsapp 8 968 814 30 80.

Источник

Парабола и касательная. Находим a,b,c!

Суть заданий следующая: дана парабола вида у = ах 2 +bх+c и касательная к этой параболе у=kх+b. Один из коэффициентов (a, b или c) неизвестен и его необходимо найти.

Как решать такие задачи? Что необходимо вспомнить?

1. Если даны уравнения двух функций, то точка (точки) пересечения их графиков находится путём решения системы этих уравнений. Пара (х;у) являющаяся решением системы есть точка пересечения графиков (или пары, если точек пересечения больше).

2. Если к графику функции проведена касательная, то производная этой функции в точке касания равна угловому коэффициенту этой касательной (см. ссылку выше).

Рассмотрим задачи (показаны два способа решения):

Прямая у=х+7 является касательной к графику функции ах 2 –15х+15. Найдите a.

Прямая и график данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения (кроме неизвестных х и у имеется ещё параметр а).

Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x_o) = k. Это третье уравнение, запишем систему:

Подставим из второго уравнения в первое:

Найдём а, подставим х = 1 в ах 2 – 15х + 15 = х + 7 или в 2ах – 15 = 1

По смыслу задачи параметр a ≠ 0, график заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах 2 – 15х + 15 = х + 7 имело единственно решение:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Прямая у=3х+1 является касательной к графику функции ах 2 +2х+3. Найдите a.

Прямая у=5х–8 является касательной к графику функции 6х 2 + bх + 16

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая и парабола пересекаются в одной точке, поэтому оба уравнения можно внести в систему, но она не решаема, так как имеем три неизвестных:

Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x o ) = k. Это третье уравнение, запишем систему:

Кратко можно сказать так:

Условия касания графика функции f (x) = k и прямой у = kх + b задаётся системой требований:

По условию, абсцисса точки касания положительна, значит х = 2.

График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение

имело единственно решение. Преобразуем:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Теперь определим, при каком значении b абсцисса точки касания будет больше нуля. Можно подставить поочерёдно полученные значения в систему:

Далее решить её и сдать вывод. Верным решением будет то значение b, при котором получим положительную абсциссу.

Но мы сразу подставим их (поочерёдно) в 28х 2 + (b – 5) + 24 = 0.

Таким образом, b = – 19 (при этом значении абсцисса точки касания положительна).

Прямая у = –5х+8 является касательной к графику функции 28х 2 + bх + 15.

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая у=–6х–2 является касательной к графику ф-ии 18х 2 +6х+с. Найдите c.

Условия касания графика функции у = f (x) и прямой у = kx + b задаётся системой требований:

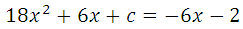
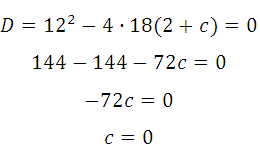
График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение имело единственное решение, преобразуем: Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю, значит: Ответ: 0

Прямая у=3х+4 является касательной к графику функции 3х 2 –3х+с. Найдите c.

Как видим, понимание способа нахождения точки пересечения графиков функций, заключающееся в решении системы, пригодилось при решении указанных задач (на ЕГЭ могут быть и другие). Но какие бы они не были, если чётко уясните геометрический смысл производной, проблем с подобными у вас не будет.

В данной рубрике продолжим рассматривать задачи, не пропустите!

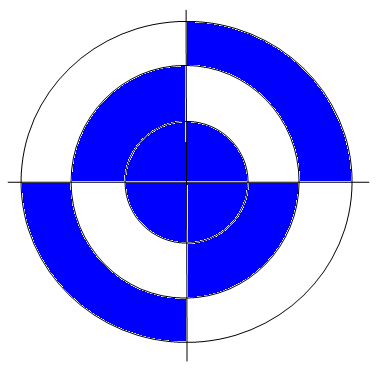
Имеется круглая мишень радиуса R. На ней отмечены две окружности, радиусы которых равны 1/3 и 2/3 от радиуса мишени. Какова вероятность того, что кинутый в мишень дротик попадёт в закрашенную часть мишени? Результат округлите до тысячных.

*Учесть, что дротик мимо мишени попасть не может.

Тот учащийся, который первый напишет верный ответ, получит поощрительный приз в размере 150 рублей 😉

Надеюсь материал был вам полезен. Успехов Вам!

Источник

Найдите положительный угловой коэффициент прямой если известно что она касается параболы

Глава 20. Парабола

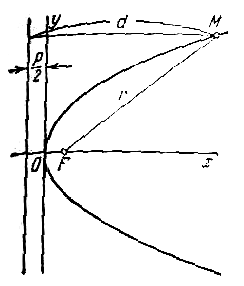
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

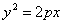
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

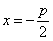
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

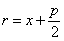
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

(2)

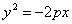
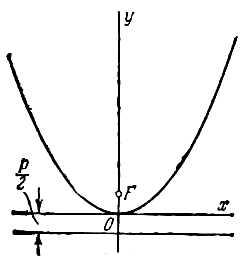
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

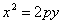
если она лежит в верхней полуплоскости (рис.), и

(4)

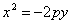
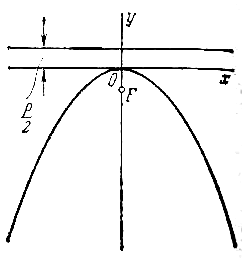
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Источник