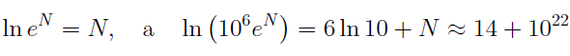К чему стремится энтропия
Энтропия? Это просто!
Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora
Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.
Так что же такое энтропия?
Энтропия — это то, как много информации вам не известно о системе
Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации. 
Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём). 
Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).
А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.
Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.
Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:
Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B. 
Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.
Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.
Физический пример: газ под поршнем
Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях. 
Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:
Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.
Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.
Твёрдые тела и потенциальная энергия
Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия. 
Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.
Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.
Понимаем второй закон термодинамики
Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад. 
Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.
Перемешивание газов
И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.
Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).
Разбираемся с демоном Максвелла
Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа. 
Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?
Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.
Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.
Просто о сложном
Энтропия. Как часто можно услышать или прочитать это красивое, умное слово. Но какой смысл оно несет в себе?
В современном же варианте она определяется как логарифм числа состояний, в которых может находиться система. Рассмотрим одну интересную особенность энтропии:
В одном кубическом метре воздуха находится
Как видите, ошибка студента в целый миллион раз никак не повлияла на определенную им энтропию системы. Вот, какое оно огромное, это число.
Пытливый ум читателя задастся вопросом: как студенту может пригодиться определенная им энтропия? Дело в том, что при равновесном состоянии система имеет наибольшее количество допустимых состояний, а значит, и наибольшую энтропию. Энтропия системы, на которую не действуют внешние факторы, всегда либо растет, либо остается постоянной, если она (система) достигла состояния равновесия. Это закон природы, который выполняется всегда, так же, как и всегда тепло передается от более горячего тела к более холодному. Существует вероятность, что тепло уйдет от холодного к горячему, но она настолько ничтожна, что это событие не произойдет никогда за все время существования нашей вселенной.
Так что же это получается, по отношению к нашему миру второй закон термодинамики не работает? Как могли образоваться сложнейшие формы жизни, что это, если не признак порядка? Согласно теории эволюции Дарвина, в основе процесса естественного отбора лежит повышение степени организованности биологических систем. Вид все более и более совершенствуется в процессе эволюции. Мы не видим в природе хаотической смеси различных атомов, расположенных вперемешку друг с другом, что соответствовало бы большему беспорядку в системе. Наоборот, мир сильно структурирован. Почему-то растут деревья, в небе плавают облака, летают какие-то бабочки. В море зачем-то плавают рыбы. Как же можно объяснить возникновение структур в открытых системах?
Все объясняется довольно просто. Рассмотрим замкнутую систему, состоящую из нескольких подсистем. Сумма их энтропий возрастает в четком соответствии со вторым законом термодинамики, но энтропия одной из подсистем при этом может убывать, не нарушая при этом никаких законов физики, а это значит, что в ней может возникать порядок.
Ставлю тег «моё», но много информации брал из лекций нашего физика, если понравится, следующий пост будет о чем-то наподобие тепловой смерти вселенной, пока не придумал.
Просто о сложном: почему все вокруг стремится к хаосу и как это остановить
Теории и практики
Когда порой вы чувствуете нарастающий уровень энтропии, но не понимаете почему, ответ кроется в физике: стремление мира к хаосу — фундаментальное свойство природы. Из чего состоит хаос, обратим ли он, можно ли его как-то измерить и почему существует выражение «ломать — не строить»? Обо всем этом T&P рассказал научный журналист, сотрудник кафедры физики и астрофизики МФТИ Айк Акопян в рамках проекта «Физтех.Читалка».
Что происходит, когда мы приводим в движение маятник? Он начинает колебаться, каждый раз уменьшая амплитуду. Через некоторое время мы обнаружим, что маятник остановился. Но куда делась энергия маятника? Те, кто в школе на уроках физики слушал учителя внимательно, ответят, что энергию заберут молекулы воздуха. Но почему не происходит обратное? Почему молекулы вдруг не могут собраться и, наоборот, передать энергию маятнику?
Дело в том, что стремление мира к хаосу оказывается фундаментальным свойством природы. Направленное движение частиц маятника превращается в хаотичное движение молекул воздуха. Направленное течение воды рано или поздно превратится в хаотичную струю с турбулентными вихрями и извивающимися, переплетающимися друг с другом потоками.
Наша природа вовсю стремится к хаосу, но неужели это стремление бесконечно? В какой момент система достигает какого-то спокойствия? В какой момент это стремление прекращается? В XIX веке Максвелл и ряд других физиков показали, что, если оставить систему в покое, она действительно придет к определенному состоянию «спокойствия». Это состояние называется равновесным, и, чтобы его понять, нужно забыть об индивидуальной скорости, координате каждой частицы и взглянуть на коллективные характеристики системы. Например, на то, сколько частиц на данный момент имеют определенные скорости.
Если мы построим график числа частиц от скорости, то увидим удивительную вещь: система из любого состояния, каким бы это состояние ни было изначально, в итоге приходит к одному определенному распределению числа частиц от скорости, которое называется распределением Максвелла. Это состояние является конечным пунктом назначения любой системы, и в ней достигается максимальный хаос.
Но… Как вообще измерить хаос? В физике для измерения хаоса используют величину, которая называется энтропией системы. Чем больше энтропия, тем менее упорядочена система. В состоянии равновесия энтропия максимальна. Больцманом в XIX веке была доказана так называемая H-теорема, которая гласит, что в замкнутой системе энтропия со временем всегда возрастает.
Не совсем. Представьте, что у вас есть замкнутая комната с кучей шариков, которые летят и врезаются друг в друга. Все абсолютно идеально, столкновения упругие, никаких потерь энергии. Через достаточное количество времени распределение скоростей будет в точности максвелловским, энтропия необратимо возрастет до максимума.
Данные телескопа Planck показали, что примерно 98% энергии нашей Вселенной не заключено в звездах и вообще в обычном веществе, из которого состоим мы
Но давайте взглянем на каждый шарик по отдельности. Дело в том, что для каждого шарика мы можем узнать в точности его скорость и координату, а также действующую на него силу. Из второго закона Ньютона можем узнать ускорение — и все: движение каждой отдельной частички можно совершенно однозначно задать. Закон Ньютона по времени обратим, так как, если повернуть время вспять, свою форму закон не изменит. Это означает, что и движение каждого отдельного шарика тоже обратимо: из конечного состояния шарика можно понять, откуда он пришел и как двигался, но… Но движение всех шариков вместе оказывается необратимым.
То есть в основе нашего необратимого мира лежат вполне себе обратимые законы. Это весьма странно. А что, если никакой необратимости нет, а это всего лишь иллюзия? Что, если движение просто настолько сложное, что оно кажется нам хаотичным, а на самом деле оно вполне регулярно?
Для примера того, что имеется в виду, возьмем очень интересную систему. Она называется клеточный автомат. Представьте, что ваша Вселенная — это простой ряд из белых и черных клеточек. Вы — бог этой Вселенной, и вам нужно заложить какое-то правило эволюции по времени. И вы закладываете очень простое правило: если сама клетка черная и соседние две клетки тоже черные, то в следующем шаге клетка будет белой (на картинке снизу слева), если клетка черная, сосед слева тоже черный, а сосед справа белый, то в следующем шаге клетка станет черной и так далее. Таким образом можно задать универсальное правило (физику) вашей Вселенной. Записать этот закон можно с помощью нулей и единичек или, если перевести их в десятиричную запись, с помощью просто одного числа. В данном случае (на картинке) это будет правило 90. Эволюция такого клеточного автомата показана ниже.
Таких правил существует очень много. Есть правила, которые опираются на два предыдущих шага вместо одного или на нескольких соседей. Есть правила для двумерного клеточного автомата, где у нас теперь не ряд из черных и белых клеточек, а целая плоскость.
С помощью клеточных автоматов уже получают совершенно сложные, непредсказуемые фигуры — их используют в архитектуре и игровом дизайне для построения реалистичного ландшафта. Но, что удивительно, все это разнообразие, эти непредсказуемые формы и образы задаются всего лишь правилом из одного числа, все остальное — дело времени.
Но что, если все разнообразие нашего мира, все сложные образы, создаваемые нашей природой, и весь тот хаос, к которому стремится наш мир, — это всего лишь реализация какого-то клеточного автомата? Что, если мы просто являемся симуляцией клеточного автомата в компьютере?
Как мы поняли в первой части, в самой глубокой основе нашего мира лежат вполне обратимые законы, где по конечному состоянию можно восстановить начальное. Поэтому если мир и есть клеточный автомат, то он должен также быть обратимым. Такие клеточные автоматы действительно есть, но у них есть одна проблема. У любого обратимого клеточного автомата есть цикл: через определенное число шагов Вселенная воссоздается в своем первоначальном виде снова, затем снова — и движется так по циклу.
В нашем мире, к сожалению, такого нет… Или есть? Французский математик Анри Пуанкаре для определенного типа систем заметил интересную вещь: в результате эволюции этих систем со временем они возвращались в свое первоначальное состояние, хотя изначально казалось, что стремятся они лишь в сторону хаоса. Такой цикл назвали циклом Пуанкаре.
Напрашивается очень интересная мысль. Да, действительно, газ из взорвавшегося гелиевого шарика в одну кучу обратно не соберется, но что, если подождать еще дольше? Что, если цикл Пуанкаре для такой системы очень большой? Есть целые космологические модели, основанные на гипотезе возврата Пуанкаре, одна из них принадлежит известному математику Пенроузу. По его мнению, Вселенная сначала раздувается, затем схлопывается обратно, затем снова взрывается, раздувается и вновь схлопывается, повторяя в точности предыдущий цикл.
Но у такой теории циклической Вселенной есть большой минус: мы пока не знаем процессов, способных заставить Вселенную схлопнуться. Где их искать? Так ли хорошо мы знаем нашу Вселенную? Данные телескопа Planck показали, что примерно 98% энергии нашей Вселенной не заключено в звездах и вообще в обычном веществе, из которого состоим мы. Мы с грехом пополам знаем лишь о 2% нашей Вселенной, а об остальных 98% не знаем вообще ничего. То есть если представить, что наша Вселенная — это большой прекрасный замок с башнями, мостами, тронными залами и прочим, то из подвала мы пока не выходили, и кто знает, какие тайны ждут нас там, наверху.
Все меняется, и некоторым из нас это не всегда нравится. Но согласно одной из точек зрения, энтропия Вселенной и природы в целом (то есть степень беспорядка или случайности в системе) может быть тем, что в первую очередь способствовало возникновению жизни.
реклама
Согласно этой точке зрения, когда группа атомов приводится в движение внешним источником энергии, например Солнцем, и окружена источником тепла, например атмосферой, она постепенно перестраивается таким образом, чтобы рассеивать все больше энергии. С этого момента, при определенных условиях, материя неумолимо приобретает свойства, ассоциирующиеся с жизнью.
Однако энтропию также связывают с тепловой смертью Вселенной. Вот все, что необходимо знать об энтропии в термодинамике и о том, как она влияет на Вселенную и, в конечном счете, на нас.
Что такое энтропия Вселенной?
Хотя в физике это не одно и то же, полезно вспомнить о теории хаоса и о том, как она связана с энтропией, и, в конечном счете, какое влияние энтропия может оказывать на Вселенную.
реклама
Согласно теории хаоса, в кажущейся случайности хаотических, сложных систем есть скрытые закономерности и взаимосвязи. Если знать начальные условия и выяснить эти базовые закономерности, то можно предсказать нарушения, которые произойдут в будущем. Другими словами, хаос не так беспорядочен и случаен, как может показаться.
В своей самой простой формулировке энтропия определяется как мера тепловой энергии в системе на единицу температуры, которая не может быть использована для совершения полезной работы. Поскольку работа получается в результате упорядоченного движения молекул, энтропия также является мерой молекулярного беспорядка, или случайности, в системе.
Не только физика, но и многие дисциплины нашли применение этой концепции, включая химию, биологию, изменение климата, социологию, экономику, теорию информации и даже бизнес.
Но давайте остановимся на физике, а точнее, на фундаментальных законах термодинамики.
Кто ввел понятие энтропии?
реклама
Несмотря на то, что понятие энтропии применяется в различных дисциплинах, оно берет свое начало в физике. Изучая сохранение механической энергии в своей работе » Основные принципы равновесия и движения» (1803), французский математик Лазар Карно предложил, что ускорения и удары движущихся частей в машине представляют собой «потери момента активности». Момент активности» Карно сопоставим с современным понятием работы в термодинамике. Таким образом, в любом естественном процессе существует неотъемлемая тенденция к рассеиванию полезной энергии.
Другие ученые исследовали эту «потерянную» энергию, и в последней половине 19 века они указали, что это не настоящее исчезновение, а преобразование. Это и есть концепция сохранения энергии, которая проложила путь к первому закону термодинамики. Такие ученые, как Джеймс Джоуль, Юлиус Майер, Герман Гельмгольц и Уильям Томпсон (также известный как лорд Кельвин), опубликовали работы, исследующие эту концепцию.
реклама
Но термин «энтропия» появился в работах немецкого физика Рудольфа Клаузиуса, который сегодня считается одним из авторов термодинамики.
В 1850-х годах он представил изложение Второго закона термодинамики применительно к тепловому насосу. Заявление Клаузиуса подчеркивало тот факт, что невозможно построить устройство, работающее по циклу и не производящее никакого другого эффекта, кроме передачи тепла от более холодного тела к более горячему.
В 1860-х годах он придумал слово «энтропия» от греческого слова, означающего превращение, или поворотный пункт, для обозначения необратимой потери тепла. Он описал ее как функцию состояния в термодинамическом цикле, в частности в цикле Карно, теоретическом цикле, предложенном сыном Лазаря Карно, Сади Карно.
В 1870-х годах австрийский физик и философ Людвиг Больцман переосмыслил и адаптировал определение энтропии к статистической механике. Ближе к тому, что подразумевает этот термин сейчас, он описывает энтропию как измерение всех возможных микро-состояний в системе, макроскопическое состояние которой было изучено. Как могут измениться все наблюдаемые свойства системы? Сколькими способами? Эти вопросы охватывают понятие беспорядка, которое лежит в основе одного из понятий энтропии.
Находится ли Вселенная в состоянии энтропии?
Еще в 19 веке Рудолф Клаузиус вывел, что энергия Вселенной постоянна, а ее энтропия имеет тенденцию к увеличению с течением времени.
По мнению космологов, затем эта точка «взорвалась», расширяясь и распространяясь со скоростью, превышающей скорость света, и породив все частицы, античастицы и излучения во Вселенной.
Конечно, для этого должно было произойти огромное количество процессов связанных с изменением энтропии. Однако если мы подумаем о непрерывном увеличении энтропии, которое происходило на протяжении всех этих лет, то сможем сделать вывод, что энтропия Вселенной сейчас должна быть намного больше. На самом деле, согласно расчетам, энтропия Вселенной сегодня примерно в квадриллион раз больше, чем во время Большого взрыва.
Почему энтропия Вселенной растет?
Черные дыры обладают огромной концентрацией массы, которая обеспечивает им исключительно сильное гравитационное поле. Поэтому они допускают множественность микросостояний. В связи с этим Стивен Хокинг предположил, что черные дыры выделяют тепловое излучение вблизи своих горизонтов событий. Это излучение Хокинга может привести к потере массы и окончательному испарению черных дыр.
Но помните, что черные дыры подчиняются второму закону термодинамики, который гласит, что энтропия всегда будет иметь тенденцию к увеличению. Поэтому они будут набирать все большую массу и сливаться с другими черными дырами, превращаясь в сверхмассивные чёрные дыры. А когда они в конце концов распадутся, излучение Хокинга, создаваемое распадающимися чёрными дырами, будет иметь такое же количество возможных состояний, как и сама ранее существовавшая черная дыра. Согласно этой точке зрения, ранняя Вселенная имела низкую энтропию из-за меньшего количества или гораздо меньших размеров черных дыр.
Существует ли предел энтропии во Вселенной?
Как бы мы ни говорили о тенденции к увеличению энтропии, законы термодинамики также подразумевают состояние максимальной энтропии.
В повседневной жизни мы можем наблюдать это, когда наш кофе остывает в чашке. Когда кофе достигает комнатной температуры, это означает, что он находится в тепловом равновесии с окружающей средой. В кипящей воде, используемой для приготовления кофе, было много возбужденных атомов, но они замедлились и в конце концов достигли максимальной энтропии для данной системы.
При постоянной, стабильной температуре во всем космосе больше не останется энергии для совершения работы, так как энтропия достигнет максимального уровня. Все эти предположения составляют теорию тепловой смерти Вселенной. Эта теория также известна под названием «Большой заморозки», поскольку в этом сценарии энтропия Вселенной будет постоянно возрастать, пока не достигнет максимального значения. В этот роковой момент все тепло в нашей Вселенной будет распределено абсолютно равномерно, не оставляя места для полезной энергии.
Может ли энтропия Вселенной уменьшиться?
Можно с уверенностью сказать, что энтропия во Вселенной в какой-то момент уменьшилась, потому что в ней существует определенный порядок. Гравитационные взаимодействия могут к примеру превращать туманности в звезды. Это своего рода порядок.
Энтропия может уменьшаться без нарушения второго закона термодинамики до тех пор, пока она увеличивается в других частях системы. В конце концов, второй закон термодинамики не говорит, что энтропия не может уменьшаться в определенных частях системы, а только то, что общая энтропия системы имеет естественную тенденцию к увеличению.
При этом общая энтропия Вселенной не уменьшается. Как было сказано выше, энтропия будет иметь тенденцию к увеличению, пока не достигнет своего максимального уровня и не приведет к тепловой смерти. Это стационарное состояние термодинамического равновесия, в котором энтропия не только максимальна, но и постоянна, и она будет оставаться такой, пока не произойдет приток энергии, который оживит систему.
Тогда цикл может повториться. С новой, дополнительной энергией, совершающей работу, останется часть энергии, не способной совершить работу, которая превратится в тепло. Это снова увеличит энтропию системы. Но откуда возьмется эта энергия? Что заставит оставшиеся лептоны и фотоны, если таковые имеются, взаимодействовать?