Как доказать что биссектрисы пересекаются в одной точке в треугольнике

Общие сведения

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих их. Точки имеют другое название — вершины. Обозначается треугольник символом Δ, после которого идут 3 латинских буквы. Например, ΔMNO. Допускается использовать и русские литеры, но злоупотреблять этим не стоит.

В высших учебных заведениях преподаватели требуют от студентов международное обозначение. Кроме того, большинство программных продуктов и онлайн-сервисов воспринимают только латинские символы.

Существует определенная классификация Δ, на основании которой доказываются теоремы, выводятся формулы, свойства и решаются задачи. В последнем случае следует правильно производить идентификацию, чтобы избежать ошибок при расчетах.

Классификация треугольников

Необходимо отметить, что Δ различаются между собой по некоторым критериям.

Они бывают нескольких типов:

В первом случае стороны фигуры не равны между собой. Чтобы идентифицировать прямоугольный треугольник, необходимо рассмотреть его углы. Если один из них является прямым (равен 90 градусам), такая фигура называется прямоугольной. В третьем виде основным критерием считается наличие двух, равных между собой сторон.

В равностороннем треугольнике все стороны равны между собой. Математики его называют «правильным». Он обладает важным свойством — вокруг него можно описать окружность. Пятый тип определяет наличие тупого угла, градусная мера которого больше 90. Если фигура является остроугольной, это значит, что все 3 его угла меньше 90, т. е. являются острыми.

Один треугольник может относиться к нескольким типам. Например, прямоугольный Δ может быть равнобедренным на основании свойства геометрии: если Δ является равнобедренным, то углы (∠), образованные боковыми сторонами с основанием, равны между собой. В этом случае их градусные меры эквивалентны 45, поскольку сумма ∠ любого Δ составляет 180. Следовательно, 180 — 90 = 2k, где неизвестная величина «к» соответствует углу при основании.

Решая уравнение, можно получить искомое значение угла: k = 45. Исходя из вычислений, треугольник является прямоугольным и равнобедренным.

Дополнительные элементы

У любого Δ существуют определенные дополнительные элементы, необходимые при построении чертежей или схематических рисунков, доказательства теорем и решения задач по геометрии.

К ним относятся:

Биссектриса — отрезок (прямая), проходящий через вершину Δ и делящий угол на 2 равные части. Медиана — единственный отрезок для каждой вершины, соединяющий ее с серединой стороны, на которую он опущен.

Высотой является перпендикуляр, опущенный из вершины на противоположную сторону.

В равнобедренном и равностороннем треугольниках биссектриса является медианой и высотой. В последнем случае их можно провести всего 3.

Теорема о биссектрисах

Теорема о биссектрисах треугольника звучит таким образом: в любом Δ биссектрисы пересекаются только в одной точке — инцентре фигуры. Для доказательства нужно построить произвольный ΔКLМ, а затем следовать по такому алгоритму:

Необходимо доказать, что третья биссектриса (МV), проведенная из вершины М, проходит через точку W. Это делается таким образом:

Далее следует рассмотреть ∠М. Следовательно, что координата точки W равноудалена от вершины М. На основании признака биссектрисы, W лежит на МV, поскольку W — точка пересечения биссектрис треугольника КLМ. Утверждение доказано.

Свойства и соотношения

На основании теоремы о биссектрисах Δ были получены некоторые важные свойства, которые рекомендуется применять при решении задач и доказательства других утверждений:

При решении задач нужно находить их длину (L).

Для удобства необходимо обозначить стороны таким образом: КМ = d, КL = e и LМ = f, чтобы воспользоваться следующими формулами через известные параметры треугольника:

Соотношения позволяют найти не только длины Lk, Lm и Ll, но и другие параметры треугольников. Следует отметить, что углы во второй группе формул соответствуют биссектрисам, исходящим из них.

Таким образом, для решения задач на нахождение длины биссектрис необходимо знать теорию, доказательство теоремы, свойства, а также основные соотношения.

Источник

Точка пересечения биссектрис треугольника – тупоугольного, правильного, остроугольного, равнобедренного

В треугольнике есть три характерные линии: высоты, медианы и биссектрисы. Для каждой из этих линий есть своя точка пересечения, характеризующая треугольник. Первой всегда изучают точку пересечения биссектрис, потому что именно она дает представление о взаимосвязи величин треугольника и связанных с ним окружностей.

Определение

Точка соединения биссектрис это одна из самых проблемных точек. Она ведет к пониманию вписанных и описанных фигур, восприятие которых очень затруднено. Приходится думать не только о треугольнике, а еще и об окружностях, вписанной и описанной, что затрудняет решение задачи.

Но с другой стороны, значения радиусов вписанной и описанной окружности фигурирует во многих формулах, что позволяет упростить решение многих задач. Но для начала разберемся, что такое вписанная и описанная окружность, а потом узнаем, как это связано с точкой пересечения биссектрис и связано ли вообще.

Рис. 1. Золотое сечение треугольника

В произвольном остроугольном треугольнике характерные точки не совпадают, а соединив их можно получить золотое сечение треугольника, для правильного треугольника золотое сечение является точкой. В равнобедренном треугольнике золотое сечение становится линией.

Вписанная окружность, это окружность, которая касается каждой из сторон треугольника.

Центр такой окружности называется инцентром треугольника. При этом, инцетр, или точка пересечения биссектрис тупоугольного треугольника всегда находится внутри треугольника, в отличие от высот.

Расстояние от инцентра до каждой из сторон одинаково и является радиусом вписанной окружности. Треугольник в таком случае будет считаться описанным вокруг окружности.

Рис. 2. Инцентр треугольника

Описанной окружностью считается окружность, касающаяся каждой из вершин треугольника. То есть, каждая вершина должна входить в границу окружности. Треугольник в этом случае наоборот будет считаться вписанным, а расстояние от вершин треугольника до центра окружности будет всегда одинаковым и равным радиусу описанной окружности.

Теоремы о точке пересечения биссектрис

Теорема, на самом деле, одна, но доказательство разбито на две части. Формулировка звучит так: биссектрисы треугольника пересекаются в одной точке и эта точка является центром вписанной окружности.

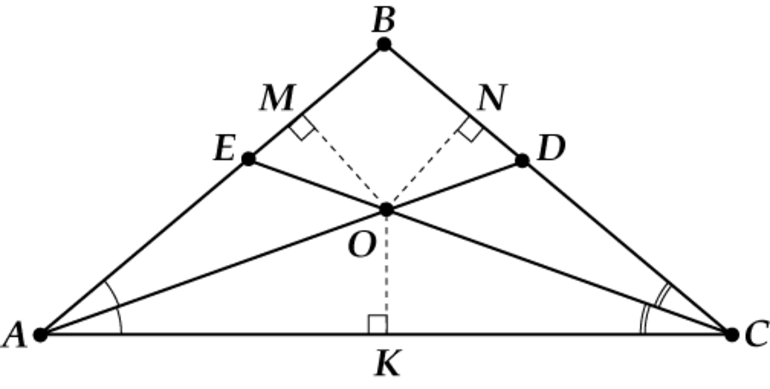
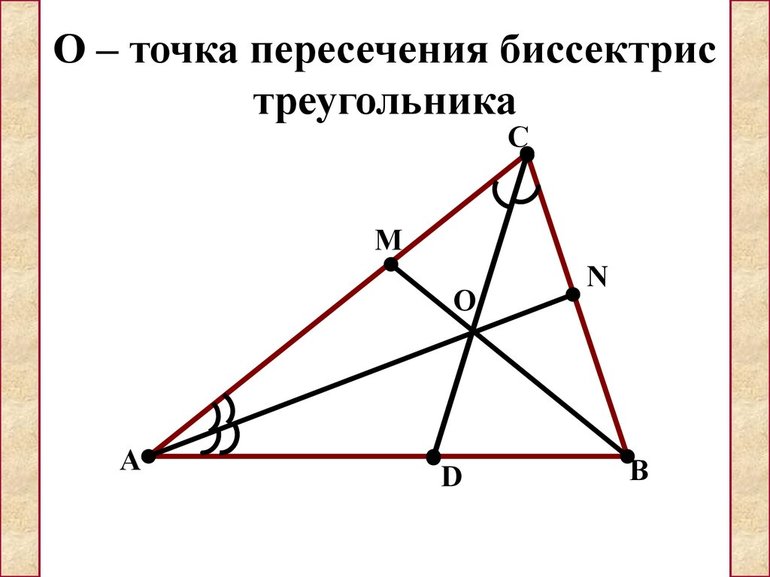
Сначала докажем, что три биссектрисы пересекаются в одной точке. Для этого в треугольнике АВС проведем биссектрисы ВМ, СР и АК. Точку пересечения обозначим О. Тогда рассмотрим каждую биссектрису в отдельности. Для биссектрисы АК расстояния до сторон треугольника а и в, должны быть одинаковы. Для биссектрисы СР расстояния с и а должны быть одинаковы. Для биссектрисы ВМ расстояния в и с должны быть одинаковы. Отрезки а, в и с равны между собой по свойству биссектрисы: любая геометрическая точка на биссектрисе равноудалена от сторон угла.

А точка равноудаленная от каждой из сторон может быть только одна. Достаточно попробовать поставить точку пересечения в другом месте и сразу станет заметно, что условие не соблюдается, что невозможно.

Рис. 3. Рисунок к задаче

Мы уже сказали, что в треугольнике только одна точка может быть равноудалена от всех сторон. Это означает, что окружность с центром в этой точке будет вписана в треугольник, так как радиус этой окружности будет перпендикулярен стороне треугольника. Теперь докажем, что в треугольнике может быть только одна вписанная окружность. Если точку о переместить в любое другое место треугольника и опустить перпендикуляры на стороны, то станет ясно, что перпендикуляры не равны между собой, а значит в этой точке центр находиться не может. Что и требовалось доказать.

Что мы узнали?

Мы узнали о точке пересечения биссектрис треугольника, выделили и доказали две части теоремы. Доказали, что в треугольнике может быть только одна вписанная окружность и узнали о золотом сечении треугольника.

Источник

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

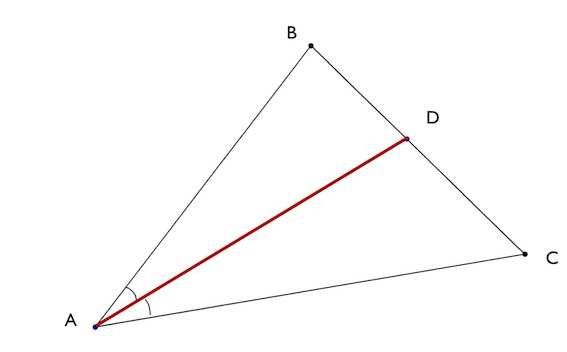
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Источник

Точка пересечения биссектрис. Свойство 1

Теорема о пересечении биссектрис в треугольнике

Биссектрисы треугольника пересекаются в одной точке.

Инцентр – точка пересечения биссектрис.

Пересечение биссектрис в треугольнике

Доказательство теоремы о пересечении биссектрис в треугольнике

Шаг 1

Рассмотрим треугольник АВС. Проведем в нем две биссектрисы АТ и ВК.

Биссектрисы АТ и ВК пересекаются. Докажем это методом от противного: пусть две биссектрисы треугольника не пересекаются. Если две прямые не пересекаются, значит, они параллельны АТ||ВК. Тогда АВ будет секущей.

Пересечение биссектрис в треугольнике. Доказательство. Шаг 1

Шаг 2

По свойству параллельных прямых сумма односторонних углов будет равна 180°, т.е.

Так как сумма всех углов треугольника равна 180 градусам, то сумма двух углов не может быть равна 360°, а значит, биссектрисы не могут быть параллельны. Следовательно, они пересекаются.

Точку пересечения двух биссектрис обозначим буквой О.

Докажем, что биссектриса угла С пересечет проведенные биссектрисы в точке О.

Пересечение биссектрис в треугольнике. Доказательство. Шаг 2

Источник