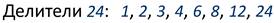Как доказать что числа взаимно простые 6 класс видеоурок
Видеоурок «Взаимно простые числа»
§ 1 Понятие взаимно простых чисел
В этом уроке Вы узнаете, какие числа называются взаимно простыми, и научитесь их определять.
Итак, что подразумевается под понятием «взаимно простые числа»?
Рассмотрим два натуральных числа 25 и 26. Это составные числа.
Натуральное число 25 делится без остатка на 1, 5, 25.
А натуральное число 26 делится без остатка на 1, 2, 13, 26.
Видим, что числа 25 и 26 имеют только один общий делитель – это число 1.
Такие числа называют взаимно простыми.
Таким образом, можно сделать вывод:
Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.
§ 2 Определение взаимно простых чисел
Даны пары натуральных чисел 14 и 28, 15 и 22.
Определим, какие из данных пар являются взаимно простыми.
Для этого необходимо определить, какие делители имеет каждое из чисел.
14 без остатка делится на 1, 2, 7, 14;
28 без остатка делится на 1, 2, 4, 7, 14, 28.
Мы видим, что числа 14 и 28, кроме единицы, имеют и другие общие делители — 2, 7, 14, а значит, не являются взаимно простыми числами.
Теперь рассмотрим другую пару чисел 15 и 22.
Число 15 делится без остатка на 1, 3, 5, 15, а число 22 делится без остатка на 1, 2, 11, 22. Мы видим, что числа 15 и 22 имеют только один общий делитель — 1.
Значит, пара натуральных чисел 15 и 22 являются взаимно простыми числами.
Теперь возьмем еще два составных натуральных числа 45 и 32.
Натуральное число 45 делится на 1, 3, 5, 9, 15, 45, а натуральное число 32 делится на 1, 2, 4, 8, 16, 32.
Видим, что эти числа имеют только один общий делитель — 1.
Значит, числа 45 и 32 являются взаимно простыми.
Разложим эти числа на простые множители. 45=3*3*5, 32=2*2*2*2*2.
Легко заметить, что взаимно простые натуральные числа 45 и 32 в разложении на простые множители не содержат одинаковых простых множителей.
Таким образом, приходим к выводу, что разложения на простые множители взаимно простых чисел не содержат одних и тех же простых множителей.
Итак, в этом уроке Вы узнали, какие числа называются взаимно простыми, а также научились определять взаимно простые числа.
Как доказать что числа взаимно простые 6 класс видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы узнаете, какие числа называются взаимно простыми, и научитесь их определять.
Итак, что подразумевается под понятием «взаимно простые числа»?
Рассмотрим два натуральных числа 25 и 26. Это составные числа.
Натуральное число 25 делится без остатка на 1, 5, 25.
А натуральное число 26 делится без остатка на 1, 2, 13, 26.
Видим, что числа 25 и 26 имеют только один общий делитель – это число 1.
Такие числа называют взаимно простыми.
Таким образом, можно сделать вывод:
Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.
Даны пары натуральных чисел 14 и 28, 15 и 22.
Определим, какие из данных пар являются взаимно простыми.
Для этого необходимо определить, какие делители имеет каждое из чисел.
14 без остатка делится на 1, 2, 7, 14;
28 без остатка делится на 1, 2, 4, 7, 14, 28.
Теперь рассмотрим другую пару чисел 15 и 22.
Значит, пара натуральных чисел 15 и 22 являются взаимно простыми числами.
Теперь возьмем еще два составных натуральных числа 45 и 32.
Натуральное число 45 делится на 1, 3, 5, 9, 15, 45, а натуральное число 32 делится на 1, 2, 4, 8, 16, 32.
Значит, числа 45 и 32 являются взаимно простыми.
Разложим эти числа на простые множители. 45=3*3*5, 32=2*2*2*2*2.
Легко заметить, что взаимно простые натуральные числа 45 и 32 в разложении на простые множители не содержат одинаковых простых множителей.
Таким образом, приходим к выводу, что разложения на простые множители взаимно простых чисел не содержат одних и тех же простых множителей.
Итак, в этом уроке Вы узнали, какие числа называются взаимно простыми, а также научились определять взаимно простые числа.
Главные понятия
Чтобы доказать, что числа взаимно простые (ВПЧ), учитываются их свойства. Запись считается правдивой, если выполняется одно из следующих условий: значение НОД равно 1, в задачах используются попарно ВПЧ. Чтобы понять слово «делитель», рассматривается конкретный пример: у 24 и 54 этот показатель равен 6. НОД может являться то число, на которое делятся без остатка m и n.
Показатель существует, и он определён, если значение m или n отлично от нуля. Понятие записывается различным набором символов. Рекомендуется следовать следующими записями:
НОД (m, n) делится на все общие делители m и n. Если соблюдается условие для а: НОД (a, b)(a, b) и для b: НОД (a, b)(a, b), значит a и b — ВПЧ. С помощью такого свойства легко определяются подходящие пары.
Составные цифры
Два числа относительно друг друга будут взаимно простыми всегда. Аналогичные отношения формируются между составными цифрами. Возможно, что из пары m или n одно — составное, а другое — простое, либо две цифры составные (натуральные числа, у которых есть больше двух делителей). Чтобы подтвердить каноническое утверждение, рассматривается пара из 9 и 88. Её простота доказывается путём вычисления НОД.
Разложение 88: ±1, ±2, ±4, ±8±1, ±2, ±4, ±8. НОД (9): ±1, ±3, ±9±1, ±3, ±9. Из двух вариантов выбираются общие цифры, а из списка определяется самая большая. Из полного перечня подходит единица.
На практике часто определяется ВПЧ двух целых цифр. Алгоритм решения задач заключается в поиске НОД, его сравнении с единицей. Чтобы быстро и правильно найти пару, используется таблица, в которой есть числа, кратные одному и сами себе.
Описание нескольких групп признаков делимости (ПД) неизвестной а:
Задачи и доказательства
Числа a1, a2, …, akу, у которых есть положительный НОД, больший 11, не являются между собой взаимно обратными. Пример с последующей проверкой: 99, 17−99, 17 и −27−27 — простые. Любое количество цифр будет ВПЧ по отношению к другим членам совокупности. Но 12, −9, 90012, −9, 900 и −72−72 к этой категории не относятся.
Первое задание
Нужно найти число из 4 цифр, кратное 15. Это не дробь, знаменателя нет, но произведение составляющих равняется 60. Решение: чтобы результат делился на 15 без остатка, он должен делиться на 3 и 5. Из предполагаемого списка вычёркивается нуль, так как произведение бы равнялось 0, что невозможно. Можно прийти к выводу, что последняя цифра результата — 5.
Известно, что в ответе должно быть четыре цифры, из которых одна уже известна. Нужно найти оставшиеся три, которые находятся в ряду перед пятёркой, а при их умножении получается 12. Проверка предположения: 60:5=12. Полученный результат легко представить в виде нескольких вариантов со следующими тремя множителями:
По условию задачи, результат должен делиться на 15. Поэтому ответ будет состоять из трёх вариантов: 3225, 2325 и 2235.
Второй пример
Из 181615121 нужно зачеркнуть 3 цифры так, чтобы результат был кратным 12. Множители делителя: 3 и 4. Если их вычеркнуть, заданное число разделится на три и четыре, что объясняется их ПД:
Учитывая ПД на 4, можно прийти к выводу, что последние две цифры из заданного числа не делятся на четыре. Поэтому из 181615121 вычёркивается единица.
Чтобы разделить 181615121 на три, необходимо просуммировать все составляющие, разделив на 3. Результат суммы равен 25 (3х8). Так как условие выполняется, вычеркивается последняя единица.
Воспользовавшись признаками делимости на 3 и 4, можно составить следующие уравнения:
Ответ: 181512, 811512 либо 181152.
Третье и четвёртое задания
Пример 3: необходимо определить шестизначное число, для записи которого используются 0 и 6, а также оно делится на 90. Решение: составляется уравнение 90 = 10х9. Результат делится на 9 и 10. В конце находится нуль, а сумма составных цифр делится на девять. Для записи используются три шестёрки, так как 3 х 6=18, а 18 кратно 9. Ответы: 666000, 660600, 606060, 600660.
Пример 4: нужно определить четырёхзначное число, которое делится на 45 без остатка. Все составные цифры разные и нечётные. Решение: следует составить уравнение с учётом условия задачи. Так как 45 = 9х5, то результат делится на пять и на девять. Одновременно он должен оканчиваться на 5, так как нуль считается чётным. Первые три цифры: 1, 3, 7, 9. Из списка выбираются те три числа, которые в сумме с пятёркой делятся на 9. К ним относятся: 1, 3, 9 и 5. Ответы: 9135, 3915,1935, 1395, 3195.
В условиях некоторых задач говорится о попарно простых числах (ППЧ). Понятие распространяется на последовательность целых цифр a1, a2, …, aka1, a2, …, ak, где каждая взаимно простая относительно других. Пример последовательности: 14, 9, 1714, 9, 17, и −25−25. Любая пара из списка будет взаимно простой. Последнее условие считается обязательным для ППЧ, но взаимно простые попарны не в каждом случае.
Другое понятие, которое встречается в задачах на рассматриваемую тему — совокупность ПЧ. Такие цифры всегда попарно и взаимно простые. Пример последовательности: 1, 443, 857, 99171, 443, 857, 991. У любой такой последовательности понятия попарности и взаимности совпадают.
Наибольший общий делитель. Взаимно простые числа
Урок 6. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Наибольший общий делитель. Взаимно простые числа»
На данном уроке мы продолжим работу с делителями числа. Напомним, что делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Рассмотрим простой случай. Саша и Маша решили украсить кабинет осенними букетами из сухих листьев. Саша собрал 12 кленовых листьев. Маша принесла 18 листьев каштана.
«А как нам узнать, какое количество букетов мы сможем составить, чтобы в каждом клиновых листьев было одинаковое количество, да и листьев каштана во всех букетах было поровну?» – спросил Саша.
«Каждое из чисел 12 и 18 должно делиться на число букетов» – ответила Маша. – «Поэтому выпишем все делители этих чисел».
Попробуем перевести эту задачу на математический язык.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.
Наибольший общий делитель двух чисел обозначается НОД (по первым буквам слов «Наибольший Общий Делитель»).
Наибольший общий делитель чисел 12 и 18 равен 6.
Теперь найдём НОД чисел 26 и 45.
Обратите внимание, что существуют числа, у которых только один общий делитель: единица. Такие числа называют взаимно простыми.
Таким образом, числа называются взаимно простыми, если у них нет общих делителей кроме единицы.
НОД взаимно простых чисел равен 1.
Чтобы находить наибольший общий делитель, не обязательно перебирать все делители чисел. В некоторых случаях это очень долгая и кропотливая работа. Существует другой способ.
Чтобы найти наибольший общий делитель двух чисел надо: разложить каждое из чисел на простые множители.
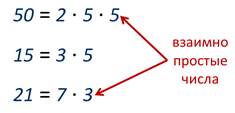
Обратите внимание, как интересно получается: сами числа составные, а вот между собой – взаимно простые.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.
Наибольший общий делитель двух чисел обозначается НОД по первым буквам слов «Наибольший Общий Делитель».
Если у нескольких чисел нет общих делителей кроме единицы, то эти числа называются взаимно простыми. НОД взаимно простых чисел равен 1.
Взаимно простые числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение взаимно простых чисел
Сначала определимся, что значит простое число.
Главное свойство простых чисел в том, что простое число делится только на единицу и на само себя.
Таких чисел немного, большинство все-таки можно разделить на другие числа. В простых числах самое важное — это деление нацело. Дробные частные и деление с остатком не рассматриваем.
Понятие взаимно простых чисел можно применить для двух целых чисел или для большего количества. Сформулируем, какие числа называются взаимно простыми.
Взаимно простые числа
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице — то есть НОД (a, b) = 1.
Проще говоря, взаимно простые числа — это целые числа, у которых нет общих делителей, кроме единицы.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать так: НОД (a, b).
Наибольший общий делитель взаимно простых чисел — это единица, что следует из определения взаимно простых чисел.
Приведем примеры взаимно простых чисел.
Заметим, что два простых числа всегда являются взаимно простыми. Однако, два числа не обязательно должны быть простыми, чтобы быть взаимно простыми. Вот такая математика в 5 классе. И еще раз: либо одно из них, либо они оба могут быть составными и при этом являться взаимно простыми. Приведем пример.
Делители 8: ±1, ±2, ±4, ±8.
На математике в 5 и 6 класса часто встречаются задания, в которых нужно доказать, что конкретные целые числа являются взаимно простыми. Из чего обычно состоит такое доказательство:
Перед вычислением НОД можно заглянуть в таблицу простых чисел и проверить, вдруг исходные целые числа можно назвать простыми. Тогда решение будет проще, так как мы знаем, что НОД простых чисел равен единице.
Повторим еще раз. Что значит взаимно простые числа? Это целые числа, у которых нет общих делителей, кроме единицы.
Пример 1
Доказать, что числа 84 и 275 являются взаимно простыми.
Сверяемся с таблицей простых чисел. 84 и 275 не являются простыми, поэтому нельзя сразу сказать об их взаимной простоте.
Вычислим НОД. Используем алгоритм Евклида для нахождения НОД:
Доказали, что числа 84 и 275 взаимно простые.
Определение взаимно простых чисел можно расширить для трех и большего количества чисел.
То есть если у некоторого набора целых чисел есть положительный общий делитель, отличный от единицы, то эти целые числа не являются взаимно простыми.
Любая совокупность простых чисел составляет набор взаимно простых чисел, например, 2, 3, 11, 19, 151, 293 и 677 — взаимно простые числа. А четыре числа 12, −9, 900 и −72 не являются взаимно простыми, так как у них есть положительный общий делитель 3. Числа 17, 85 и 187 тоже не взаимно простые, потому что каждое из них можно разделить на 17.
Как определить взаимно простые числа:
Пример 2
Являются ли числа 331, 463 и 733 взаимно простыми?
Заглянем в таблицу простых чисел. Видим, что 331, 463 и 733 — простые. Значит, у них есть единственный положительный общий делитель — единица. Поэтому, 331, 463 и 733 есть взаимно простые числа.
Пример 3
Доказать, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.
Найдем НОД заданных чисел и убедимся, что он не равен единице.
Делители целых отрицательных чисел совпадают с делителями соответствующих противоположных чисел. Поэтому НОД (−14, 105, 2 107, −91) = НОД (14, 105, 2 107, 91). Посчитаем:
НОД (14, 105, 2 107, 91) = 7.
Мы получили, что наибольший общий делитель исходных чисел равен семи, поэтому эти числа не являются взаимно простыми. Доказали.
Свойства взаимно простых чисел
У взаимно простых чисел есть определенные свойства. Рассмотрим основные свойства взаимно простых чисел.
Свойство 1
Числа, которые получились при делении целых чисел a и b на их наибольший общий делитель, называются взаимно простыми. То есть, a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Это свойство взаимно простых чисел помогает находить пары взаимно простых чисел. Для этого достаточно взять два любых целых числа и разделить их на наибольший общий делитель. В результате получим взаимно простые числа.
Свойство 2
Докажем эту необходимость:
Пусть числа a и b взаимно простые. Тогда по определению взаимно простых чисел НОД (a, b) = 1. А из свойств НОД мы знаем, что для целых чисел a и b верно соотношение Безу au0 + bv0 = НОД (a, b). Следовательно, au0 + bv0 = 1.
Соотношение Безу — представление НОД целых чисел в виде их линейной комбинации с целыми коэффициентами.
Докажем достаточность:
Свойство 3
Если числа a и b взаимно простые, и произведение ac делится на b — значит c делится на b.
Действительно, так как a и b взаимно простые, то из предыдущего свойства у нас есть равенство au0 + bv0 = 1. Если умножть обе части этого равенства на c, получится acu0 + bcv0 = c.
Первое слагаемое суммы acu0 + bcv0 делится на b, так как ac делится на b по условию, второе слагаемое этой суммы также делится на b, так как один из множителей равен b. Можно сделать вывод, что вся сумма делится на b. А так как сумма acu0 + bcv0 равна c, то и c делится на b.
Свойство 4
Если числа a и b взаимно простые, то НОД (ac, b) = НОД (c, b).
Покажем, во-первых, что НОД (ac, b) делит НОД (c, b), а во-вторых, что НОД (c, b) делит НОД (ac, b), это и будет доказывать равенство НОД (ac, b) = НОД (c, b).
НОД (ac, b) делит и ac и b, а так как НОД (ac, b) делит b, то он также делит и bc. То есть, НОД (ac, b) делит и ac и bc, следовательно, в силу свойств наибольшего общего делителя он делит и НОД (ac, bc), который по свойствам НОД равен c * НОД (a, b) = c. Таким образом, НОД (ac, b) делит и b и c, следовательно, делит и НОД (c, b).
С другой стороны, НОД (c, b) делит и c и b, а так как он делит с, то также делит и ac. Поэтому НОД (c, b) делит и ac и b, следовательно, делит и НОД (ac, b).
Так мы показали, что НОД (ac, b) и НОД (c, b) взаимно делят друг друга, значит, они равны.
Свойство 5
Предыдущее свойство взаимно простых чисел поможет намзаписать ряд равенств вида:
Определение попарно простых чисел
Через взаимно простые числа можно дадим определение попарно простых чисел.
Приведем пример попарно простых чисел.
При этом, взаимно простые числа далеко не всегда могут быть попарно простыми. Подтвердим на примере. 8, 16, 5 и 15 не являются попарно простыми, так как числа 8 и 16 не взаимно простые. Однако, 8, 16, 5 и 15 — взаимно простые. Таким образом, 8, 16, 5 и 15 — взаимно простые, но не попарно простые.
Остановимся на понятии совокупности некоторого количества простых чисел. Эти числа всегда являются и взаимно простыми и попарно простыми. Например, 71, 443, 857, 991 — и попарно простые, и взаимно простые.
Когда речь идет о двух целых числах, то для них понятия «попарно простые» и «взаимно простые» совпадают.