Как доказать что числа взаимно простые видеоурок
Как доказать что числа взаимно простые видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке Вы узнаете, какие числа называются взаимно простыми, и научитесь их определять.
Итак, что подразумевается под понятием «взаимно простые числа»?
Рассмотрим два натуральных числа 25 и 26. Это составные числа.
Натуральное число 25 делится без остатка на 1, 5, 25.
А натуральное число 26 делится без остатка на 1, 2, 13, 26.
Видим, что числа 25 и 26 имеют только один общий делитель – это число 1.
Такие числа называют взаимно простыми.
Таким образом, можно сделать вывод:
Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.
Даны пары натуральных чисел 14 и 28, 15 и 22.
Определим, какие из данных пар являются взаимно простыми.
Для этого необходимо определить, какие делители имеет каждое из чисел.
14 без остатка делится на 1, 2, 7, 14;
28 без остатка делится на 1, 2, 4, 7, 14, 28.
Теперь рассмотрим другую пару чисел 15 и 22.
Значит, пара натуральных чисел 15 и 22 являются взаимно простыми числами.
Теперь возьмем еще два составных натуральных числа 45 и 32.
Натуральное число 45 делится на 1, 3, 5, 9, 15, 45, а натуральное число 32 делится на 1, 2, 4, 8, 16, 32.
Значит, числа 45 и 32 являются взаимно простыми.
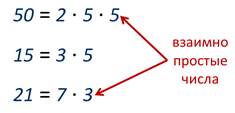
Разложим эти числа на простые множители. 45=3*3*5, 32=2*2*2*2*2.
Легко заметить, что взаимно простые натуральные числа 45 и 32 в разложении на простые множители не содержат одинаковых простых множителей.
Таким образом, приходим к выводу, что разложения на простые множители взаимно простых чисел не содержат одних и тех же простых множителей.
Итак, в этом уроке Вы узнали, какие числа называются взаимно простыми, а также научились определять взаимно простые числа.
Как доказать что числа взаимно простые видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке Вы узнаете, какие числа называются взаимно простыми, и научитесь их определять.
Итак, что подразумевается под понятием «взаимно простые числа»?
Рассмотрим два натуральных числа 25 и 26. Это составные числа.
Натуральное число 25 делится без остатка на 1, 5, 25.
А натуральное число 26 делится без остатка на 1, 2, 13, 26.
Видим, что числа 25 и 26 имеют только один общий делитель – это число 1.
Такие числа называют взаимно простыми.
Таким образом, можно сделать вывод:
Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.
Даны пары натуральных чисел 14 и 28, 15 и 22.
Определим, какие из данных пар являются взаимно простыми.
Для этого необходимо определить, какие делители имеет каждое из чисел.
14 без остатка делится на 1, 2, 7, 14;
28 без остатка делится на 1, 2, 4, 7, 14, 28.
Теперь рассмотрим другую пару чисел 15 и 22.
Значит, пара натуральных чисел 15 и 22 являются взаимно простыми числами.
Теперь возьмем еще два составных натуральных числа 45 и 32.
Натуральное число 45 делится на 1, 3, 5, 9, 15, 45, а натуральное число 32 делится на 1, 2, 4, 8, 16, 32.
Значит, числа 45 и 32 являются взаимно простыми.
Разложим эти числа на простые множители. 45=3*3*5, 32=2*2*2*2*2.
Легко заметить, что взаимно простые натуральные числа 45 и 32 в разложении на простые множители не содержат одинаковых простых множителей.
Таким образом, приходим к выводу, что разложения на простые множители взаимно простых чисел не содержат одних и тех же простых множителей.
Итак, в этом уроке Вы узнали, какие числа называются взаимно простыми, а также научились определять взаимно простые числа.
Наибольший общий делитель. Взаимно простые числа
Урок 6. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Наибольший общий делитель. Взаимно простые числа»
На данном уроке мы продолжим работу с делителями числа. Напомним, что делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Рассмотрим простой случай. Саша и Маша решили украсить кабинет осенними букетами из сухих листьев. Саша собрал 12 кленовых листьев. Маша принесла 18 листьев каштана.
«А как нам узнать, какое количество букетов мы сможем составить, чтобы в каждом клиновых листьев было одинаковое количество, да и листьев каштана во всех букетах было поровну?» – спросил Саша.
«Каждое из чисел 12 и 18 должно делиться на число букетов» – ответила Маша. – «Поэтому выпишем все делители этих чисел».
Попробуем перевести эту задачу на математический язык.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.
Наибольший общий делитель двух чисел обозначается НОД (по первым буквам слов «Наибольший Общий Делитель»).
Наибольший общий делитель чисел 12 и 18 равен 6.
Теперь найдём НОД чисел 26 и 45.
Обратите внимание, что существуют числа, у которых только один общий делитель: единица. Такие числа называют взаимно простыми.
Таким образом, числа называются взаимно простыми, если у них нет общих делителей кроме единицы.
НОД взаимно простых чисел равен 1.
Чтобы находить наибольший общий делитель, не обязательно перебирать все делители чисел. В некоторых случаях это очень долгая и кропотливая работа. Существует другой способ.
Чтобы найти наибольший общий делитель двух чисел надо: разложить каждое из чисел на простые множители.
Обратите внимание, как интересно получается: сами числа составные, а вот между собой – взаимно простые.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.
Наибольший общий делитель двух чисел обозначается НОД по первым буквам слов «Наибольший Общий Делитель».
Если у нескольких чисел нет общих делителей кроме единицы, то эти числа называются взаимно простыми. НОД взаимно простых чисел равен 1.
Взаимно простые числа – какие, примеры, определение, таблица (6 класс, математика)
Взаимно простые числа тема достаточно сложная тема 6 класса математики. Как и простые числа, тема взаимно простых чисел используется для сложения и вычитания дробей. Чтобы не допускать ошибок в этой теме разберемся в вопросе подробнее.
Простые числа
Что такое простое число? Простое число делится только на ноль и на само себя. Например, число 13 является простым, так как нацело делится только на 1 и на 13. Секрет в том, что практически каждое число можно разделить на другое число. Но в простых числах важно именно деление нацело, дробные частные и деление с остатком не рассматривается.
Простые числа в знаменателях дробей означают, что для нахождения общего знаменателя нужно перемножить эти числа между собой. Разложить простые числа на множители невозможно. Поэтому НОД двух простых чисел это их произведение.
Числа, которые содержат в себе больше двух множителей, то есть делятся на несколько чисел, называются сложными. Сложные числа состоят из перемноженных простых.
Взаимно простые числа
Взаимно простыми числами называются числа, наибольший общий делитель которых равен единицы. Доказать факт того, что числа являются взаимно простыми можно только с помощью разложения чисел на простые множители. Если у чисел нет общих множителей, кроме 1, то они будут взаимно простыми.
При этом сами по себе взаимно простые числа могут быть сложными. Важен именно НОД двух чисел.
Нужно учитывать, что взаимно простыми могут быть не только два числа, но и 3, 4, 10 – любое множество чисел может быть взаимно простым.
Как определить взаимно простые числа?
Для того чтобы определить взаимно простые числа, можно воспользоваться двумя алгоритмами:
Относительно друг друга два простых числа всегда будут взаимно простыми. А если одно из чисел, делится на другое нацело, то эти числа точно не являются взаимно простыми.
Пример
Определим, являются ли взаимно простыми числа 1729 и 282
Определение начинается с разложения на множители:
Обратите внимание, что для разложения таких чисел придется использовать метод перебора. Согласно таблице простых чисел каждый множитель проверяется, после чего деление продолжается. Подбирать множители нужно от маленьких чисел к большим, то есть от 2 и выше.
Как видно, общих множителей у двух чисел нет. Это значит, что числа можно считать взаимно простыми. Не нужно пугаться, если среди множителей попадаются достаточно большие числа. Среди учеников существует миф, что простые числа редко бывают больше 20, это не так. Просто такие числа проще использовать в задачах, чтобы набить руку. На экзамене или в контрольной сложность числа для разложения может быть абсолютно любой
Что мы узнали?
Мы поговорили о простых числах. Выяснили, что такое взаимно простые числа и обговорили некоторые их свойства. Привели примеры взаимно простых чисел. Обговорили неправильные мнения по поводу простых и взаимно простых чисел.
Видеоурок «Взаимно простые числа»
§ 1 Понятие взаимно простых чисел
В этом уроке Вы узнаете, какие числа называются взаимно простыми, и научитесь их определять.
Итак, что подразумевается под понятием «взаимно простые числа»?
Рассмотрим два натуральных числа 25 и 26. Это составные числа.
Натуральное число 25 делится без остатка на 1, 5, 25.
А натуральное число 26 делится без остатка на 1, 2, 13, 26.
Видим, что числа 25 и 26 имеют только один общий делитель – это число 1.
Такие числа называют взаимно простыми.
Таким образом, можно сделать вывод:
Натуральные числа называются взаимно простыми, если их наибольший общий делитель равен 1.
§ 2 Определение взаимно простых чисел
Даны пары натуральных чисел 14 и 28, 15 и 22.
Определим, какие из данных пар являются взаимно простыми.
Для этого необходимо определить, какие делители имеет каждое из чисел.
14 без остатка делится на 1, 2, 7, 14;
28 без остатка делится на 1, 2, 4, 7, 14, 28.
Мы видим, что числа 14 и 28, кроме единицы, имеют и другие общие делители — 2, 7, 14, а значит, не являются взаимно простыми числами.
Теперь рассмотрим другую пару чисел 15 и 22.
Число 15 делится без остатка на 1, 3, 5, 15, а число 22 делится без остатка на 1, 2, 11, 22. Мы видим, что числа 15 и 22 имеют только один общий делитель — 1.
Значит, пара натуральных чисел 15 и 22 являются взаимно простыми числами.
Теперь возьмем еще два составных натуральных числа 45 и 32.
Натуральное число 45 делится на 1, 3, 5, 9, 15, 45, а натуральное число 32 делится на 1, 2, 4, 8, 16, 32.
Видим, что эти числа имеют только один общий делитель — 1.
Значит, числа 45 и 32 являются взаимно простыми.
Разложим эти числа на простые множители. 45=3*3*5, 32=2*2*2*2*2.
Легко заметить, что взаимно простые натуральные числа 45 и 32 в разложении на простые множители не содержат одинаковых простых множителей.
Таким образом, приходим к выводу, что разложения на простые множители взаимно простых чисел не содержат одних и тех же простых множителей.
Итак, в этом уроке Вы узнали, какие числа называются взаимно простыми, а также научились определять взаимно простые числа.