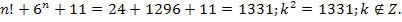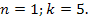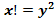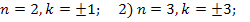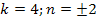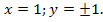Как доказать что число не может быть полным квадратом
До этого была аналогичная задача с числом 3959604. Но для этого числа все просто. Берем число, делим сначала на наименьшее простое, т.е. 2 (проверяя предварительно признак делимости). Получаем частное. Частное опять проверяем на признак делимости на 2. Если нет. То проверяем, делится ли частное на следующее простое, т.е. 3. Если делится, делим. И т.д. В итоге получаем разложение на простые 3959604 = 2 * 2 * 3 * 3 * 3 * 3 * 11 * 11 * 101. Воспользуемся свойством. Квадрат любого целого числа содержит четное число простых сомножителей (все его простые множители имеют чётные кратности). Поэтому число 3959604 не может быть квадратом целого.
задан 6 Дек ’20 22:27
остаток от деления на 3 равен 2. а такого не бывает для полных квадратов.
@vadimm: число, оканчивающееся на 06, чётно, но не делится на 4. То есть числа вида 4n+2 квадратами не являются. Это соображение вполне годится для пятиклассника.
Второй вопрос существенно сложнее, так как там надо что-то считать. Но в принципе идея вполне понятная. Там ещё работает идея рассмотрения остатков от деления на 7, но это уже для классов постарше.
Спасибо. Но почему так получается это нужно доказать. Как это объяснить 5-ти класснику? Тут методический и педагогический вопрос.
@falcao, спасибо. Но вот не очень понятно. Числа вида 4n+2 и 23579006. Почему не является?
то есть остатка 2 у квадратов не получается.
Если брать эти свойства, то ребенку надо будет доказывать, наверное. Квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей. Квадрат числа либо делится на 4, либо при делении на 8 даёт остаток 1. Квадрат числа либо делится на 9, либо при делении на 3 даёт остаток 1.
Для 3959604. Делится на 9. Но квадратом не является.
Не понятно. Почему это число вида 4n+2? Как ребенок должен понять, догадаться?
Забудьте про 4n+2. Каждое простое должно входить четное число раз. Если выделили какое-то одно, в данном случае 2, то число должно делиться на него четное число раз. Если нашли простое число, которое не входит четное число раз, то точно не квадрат. Полное разложение на простые не нужно.
@spades, кажется, понял. Число 23579006 делится на 2 (определяем по признаку делимости на 2). Делим 23579006 на 2. Получаем 11789503. Смотрим по признаку делимости делится ли 11789503 опять на 2. Нет. Дальше можно не продолжать. Так как сомножитель 2 будет всего один, а нужно чтобы было четное количество каждого сомножителя. Доказательство завершено. Так?
Свойства квадрата целого числа
Применение свойств квадрата целого числа в решении задач на делимость
Разделы: Преподавание математики
Цель:формирование знаний, умений и навыков при решении в целых числах уравнений, содержащих квадрат целого числа; создание условий для преодоления у выпускников трудностей при решении заданий ( 
Задачи:
Тип занятия: урок изучения нового материала.
Ход урока
I. Постановка цели
В 2009-2010 учебном году на ЕГЭ по математике задания 
II. Актуализация опорных знаний
При решении задач нам пригодятся признаки делимости чисел, с которыми вы познакомились ещё в 6-ом и последующих классах, а также определение числа
Напомните, пожалуйста, признаки делимости:
И ещё вопрос: что такое 
n! = 1 






1! = 1
2! = 1 
3! = 1 

4! = 1 


5! = 1 



6! =1 




При n≥5 число n! всегда оканчивается нулём.
III. Ознакомление с новым материалом
Рассмотрим таблицу квадратов натуральных чисел. Все свойства точного квадрата числа спрятаны в этой таблице. Нам только надо проявить наблюдательность при анализе данных в таблице.
| к | … |
 | … |
Обратите внимание на последние цифры квадратов чисел. Что вы заметили?
На какие натуральные числа может делиться точный квадрат числа?
Свойства квадрата целого числа
1. Точный квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей.
Первое свойство очевидное и доказательства не требует.
2. Квадрат натурального числа либо делится на 4, либо при делении на 8 даёт остаток 1.
Доказательство:
Если а – число чётное, то есть а = 2к, то 


Если а – число нечётное, то есть а = 2к + 1, то 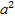
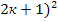

3. Квадрат натурального числа либо делится на 9, либо при делении на 3 даёт остаток 1.
Доказательство:
Если число а кратно 3, значит а = 3к, тогда 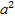


Если же число а не кратно 3, то оно имеет вид а = 3к ± 1, тогда 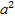


Вот мы и сформулировали свойства точного квадрата числа. Теперь вашему вниманию я предлагаю ряд задач, в решении которых используются вышеперечисленные свойства.
1. Найти все натуральныеn, при которых число 
Решение:
Если n=1, то 
Если n=2, то 
Если n=3, то 
Если n=4, то 

Если 


Ответ: при n=4.
Эта задача могла быть сформулирована иначе:
Решить в целых числах уравнение 
Способ решения тот же. Только надо помнить, что по определению
Ответ: 
2. Решить в целых числах уравнение: 
Решение:
Так как 


Если n=1, то 
Если n=2, то 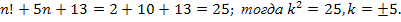
Если n=3, то 
Если n=4, то 
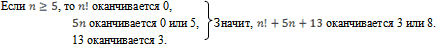
Но по свойству (1) квадрат целого числа не может оканчиваться ни 3, ни 8, значит, других целых решений уравнение не имеет.
Ответ: 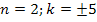
3. Решить в целых числах уравнение: 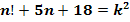
Решение:
В решении этого уравнения надо использовать тот же приём, что и в предыдущих. Его легко решить устно.
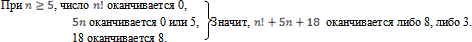
Но тогда 


Если n=1, то 
Если n=2, то 
Если n=3, то 
Если n=4, то 
Как видим, ни при каком 

Ответ:уравнение не имеет целых решений.
4. Решить уравнение в целых числах: 
Решение:


Значит, 

Но квадрат целого числа не может оканчиваться 7, значит, 
Значит, решения уравнения следует искать при 
Если n=1, то 
Если n=2, то 
Если n=3, то 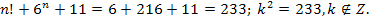
Если n=4, то
Ответ: 
5. Решить в натуральных числах уравнение 
Решение:
В этом уравнении 

Но квадрат целого числа не может оканчиваться 3, значит, при 

Если n=1, то 
Если n=2, то 
Если n=3, то 
Если n=4, то
Ответ:
6. Решить уравнение в целых числах: 1!+2!+3!+…+
Решение:
Если 


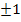
Если 


Если 




Если 

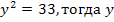
Если 
Значит, при
Ответ: 



7. Доказать, что уравнение 
Доказательство:

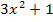
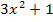

Но квадрат целого числа не может оканчиваться ни цифрой 3, ни цифрой 8.
Значит, уравнение не имеет целых решений. Что и требовалось доказать.
8. Решить в целых числах уравнение 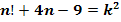
Решение:
Если n=1, то 
Если n=2, то 
Если n=3, то 
Если n=4, то 
Если 
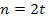












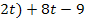
=1 




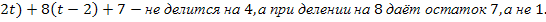
При нечётном 












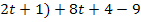






Ответ: 1)
9. Решить уравнение в целых числах: 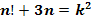
Решение:
Если 


Если 

При 







Но 






Ответ: 1) 

10. Решить в целых числах уравнение:
Решение:
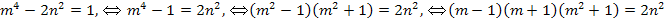
1) Если m – число чётное, то 


2) Если m – число нечётное, то 
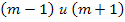



Ответ: 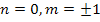
11. Решить в целых числах уравнение:
Решение:

1) Если n – число четное, то 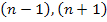




2) Если n – число нечётное, то – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда их произведение 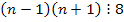






При 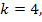


Если же 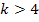
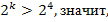

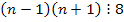
Ответ: 1) 
12. Решить в целых числах уравнение:
Решение:

1) 




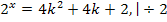

( 





Ответ: 1) 
13. Доказать, что число, оканчивающееся двумя одинаковыми цифрами, отличными от 0 и 4, не может быть точным квадратом.
Доказательство:
Так как квадрат любого числа может оканчиваться цифрами: 0; 1; 4; 5; 6; 9, то кроме 0 и 4 последними цифрами могут быть: 11; 55; 66; 99.




Значит, не существует таких чисел