Как доказать что диагонали равны
Диагонали прямоугольника равны
Здравствуйте!
Изучали свойство: «диагонали прямоугольника равны». Как его доказать?
Спасибо!
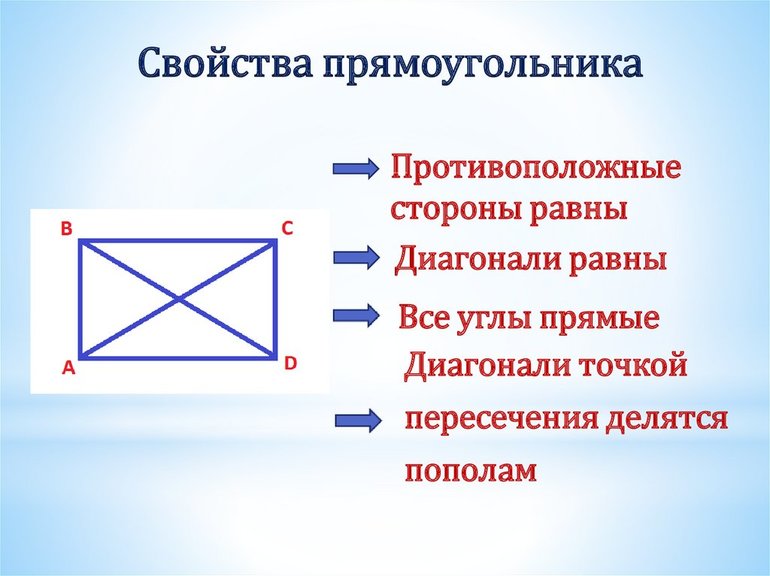
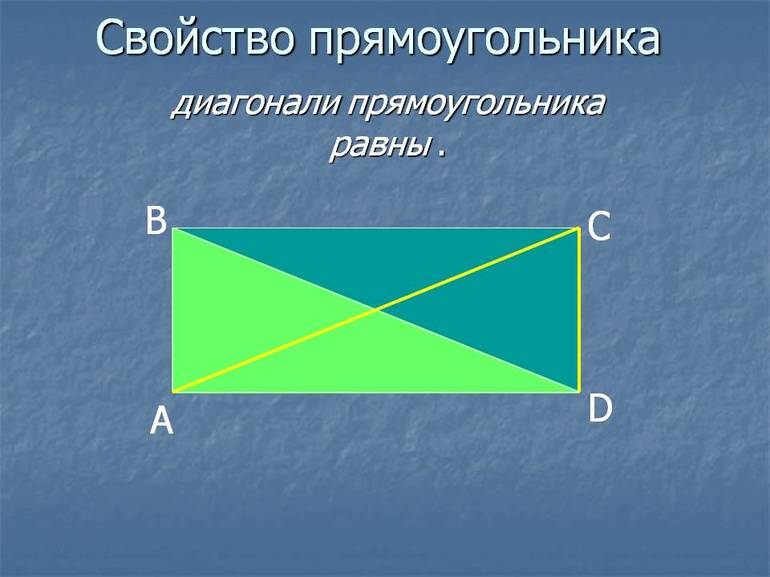
Основное свойство диагоналей прямоугольника заключается в том, что диагонали прямоугольника равны.
Докажем это свойство.
Доказательство.
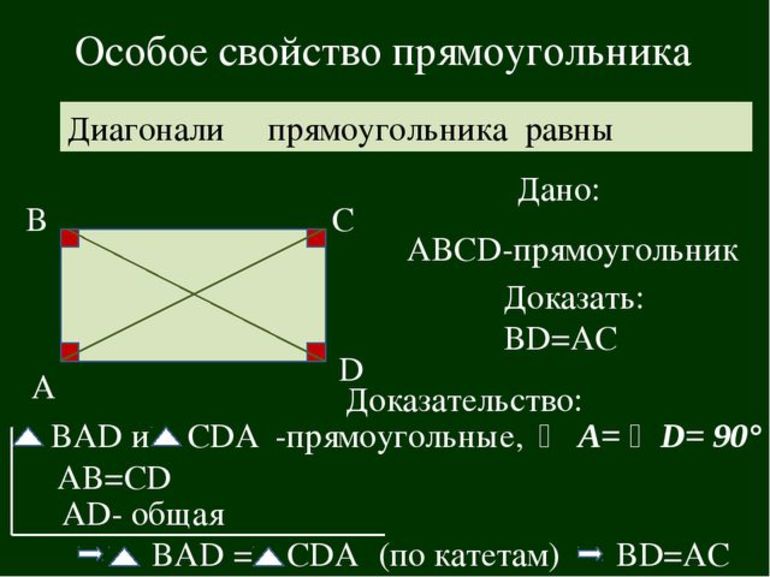
Рассмотрим прямоугольник ABCD. Он имеет две диагонали AC и BD. 
Докажем, что диагональ AC равна диагонали BD.
Рассмотрим треугольники ABD и АСD. Они являются прямоугольными, поскольку прямоугольник имеет прямые углы, то есть угол BAD и угол ADC равны по 90 градусов. 
Катеты AB и СD этих двух треугольников равны (поскольку равны противолежащие стороны прямоугольника).
Катет AD у треугольников общий.
Следовательно, по двум катетам и углу (прямому) между ними треугольники ABD и АСD равны.
Поскольку рассмотренные треугольники равны, то и все их стороны равны. Следовательно сторона AC равна стороне BD, а это не что иное, как диагонали нашего прямоугольника.
Таким образом, мы доказали, что у прямоугольника равные диагонали.
Доказательство завершено.
Это свойство также имеет квадрат, равнобедренная трапеция и, пожалуй, никакие другие четырехугольники. Конечно же, не беря во внимание частные случаи. Хотя, если говорить, например, о ромбе, то он будет иметь равные диагонали только в одном случае – при равных сторонах. Но в таком случае ромб будет являться квадратом.
Общая информация
В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.
Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.
Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.
Сведения о прямоугольнике
Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.
Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.
Идентификация или признаки
Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:
Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:
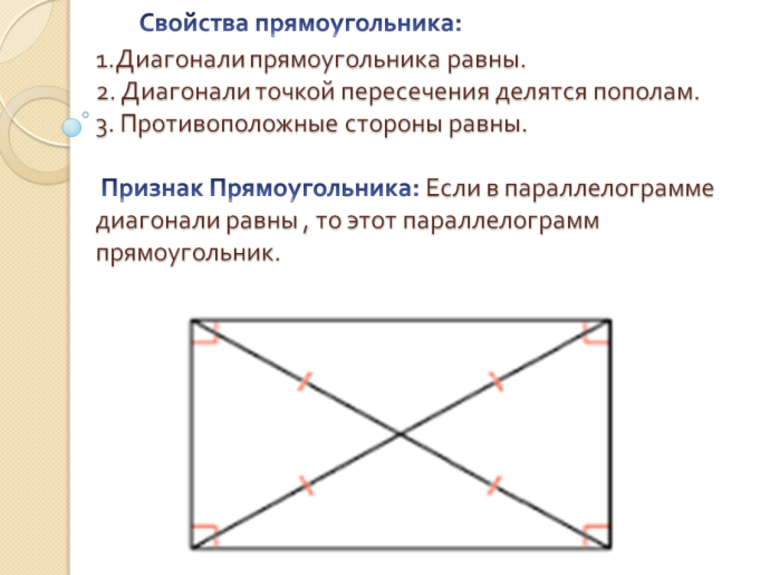
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.
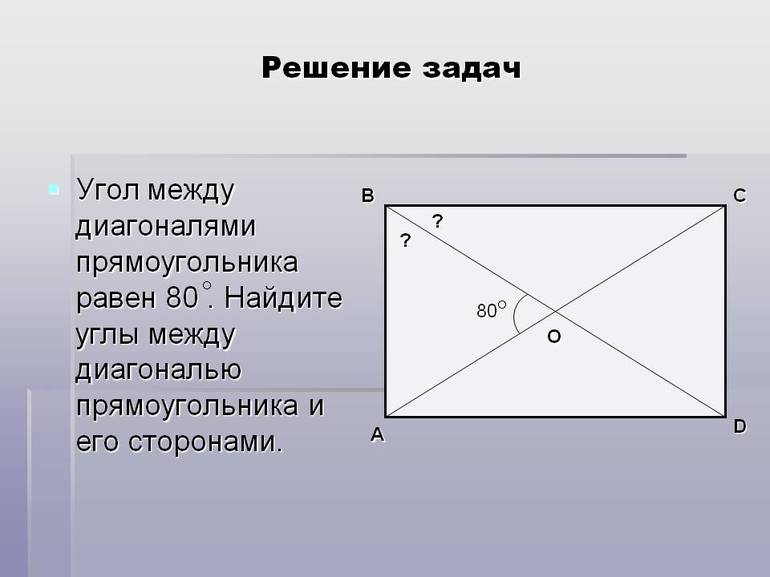
Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.
Свойства фигуры
Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB 2 + BC 2 )^(½). При решении задач применяются свойства прямоугольника:
Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).
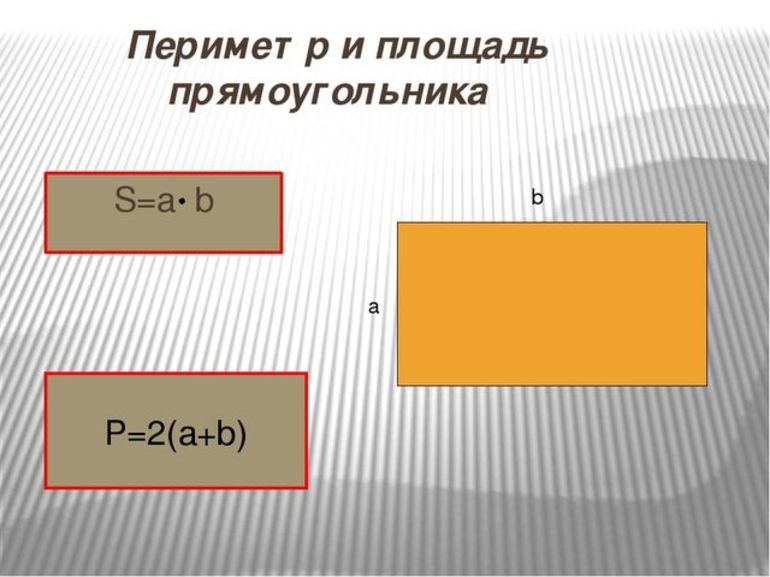
Периметр и площадь
Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:
P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.
a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].
Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.
R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].
D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].
Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.
Диагонали и стороны
Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:
Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:
a и b: d = [a 2 + b 2 ]^(1/2).
S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.
P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.
Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.
Другие соотношения
Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:
a и b: R = (a 2 + b 2 )^(1/2) / 2.
P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.
S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.
Пример решения
Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:
Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.
У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.
Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:
R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).
R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).
Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.
Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.
Свойства диагоналей ромба — основные формулы и доказательство теоремы
При решении математических и физических задач необходимо уметь правильно находить некоторые параметры ромба. Свойства диагоналей могут уменьшить количество и время вычислений. Однако в интернете информация не систематизирована. Кроме того, некоторые сайты наполняются ошибочными данными, которые и путают новичков. Специалисты предлагают специальный алгоритм, помогающий в решении. Однако для этого следует ознакомиться с теорией.
Общие сведения
На начальных этапах при расчетах следует правильно опознать фигуру. Для каждого геометрического тела существуют основные признаки, по которым она идентифицируется. Кроме того, некоторые параметры взаимосвязаны между собой некоторыми зависимостями. У каждой из них есть такие характеристики: размер сторон, углы, периметр, площадь, а также свойства, полученные при доказательстве теорем.
В любой дисциплине с физико-математическим уклоном существуют аксиомы и теоремы. Первые не требуют доказательства, а для вторых — оно необходимо. Последние доказываются на основании аксиом или доказательств других теорем. При изучении какой-либо фигуры следует начинать с определения, исходя из которого можно получит некоторую важную информацию.
Информация о ромбе
Ромбом называется параллелограмм, который имеет равные стороны. Частным его случаем считается квадрат, у которого внутренние углы при вершинах прямые. Фигуры отличаются размером сторон и углами. Однако для всего типа действуют признаки и свойства. Некоторые путают эти два термина. Однако они существенно отличаются между собой.
С помощью признаков можно правильно распознать фигуру, а потом применить необходимые формулы для решения задач. Свойства используются только после идентификации. Они позволяют вычислить некоторые параметры или доказать теоремы. Достаточно двух признаков для точного определения типа фигуры.
Чтобы не запутаться в терминологии математики предлагают простые определения. Признаками является характерные параметры, которые присущи определенному типу геометрического тела. Свойства — совокупность утверждений, которые применяются для нахождения параметров, величин, доказательства тождеств и решения уравнений.
Основные признаки
Ромб имеет такие же признаки, как и параллелограмм. Однако существуют некоторые критерии, по которым можно отличить эти две фигуры:
Однако под эти признаки попадает не только ромб, но и квадрат. Существует специальный алгоритм, позволяющий выяснить принадлежность четырехугольника к той или иной группе. Он состоит из следующих шагов:
Например, у четырехугольника с прямыми внутренними углами диагонали пересекаются в некоторой точке, и образуют 4 треугольника с прямым углом. Следует идентифицировать тип фигуры. Для этого нужно воспользоваться вышеописанным алгоритмом:
Алгоритм является очень простым. При его применении не возникает проблем вообще.
При использовании признаков и алгоритма специалисты-математики гарантируют точность определения. После идентификации фигуры необходимо обратить внимание на ее свойства.
Важные свойства
Ромб обладает всеми свойствами параллелограмма, которые следует учитывать. Ошибка некоторых новичков заключается в том, что они при поиске свойств не обращают внимания на частные случаи. Из-за невнимательности некоторые задачи решаются очень долго, а иногда произвести вычисления просто невозможно. К основным свойствам параллелограмма относятся следующие:
Ромб обладает также свойствами, которые присущи только ему. Это связано с тем, что он является частным случаем класса параллелограммов. К ним необходимо отнести следующие:
Некоторые из свойств были получены при доказательстве теорем. Для выведения третьего свойства использовалась теорема Пифагора.
Теоремы о диагоналях
В геометрии всего две теоремы о диагоналях ромба. Для удобства их можно объединить в одну с такой формулировкой: диагонали ромба взаимно перпендикулярны и являются биссектрисами внутренних углов фигуры. Для доказательства следует рассмотреть сначала первое свойство, которое называется теоремой о свойстве диагоналей ромба.
Для этого необходимо начертить произвольный ромб ABCD с диагоналями, которые будут обозначаться АС = d1 и BD = d2. Они пересекаются в некоторой точке W. По восьмому свойству параллелограмма: AW = CW, т. е. они будут делиться на два равных отрезка (половина длины диагонали).
После этого нужно рассмотреть треугольник ABC, который является равнобедренным по определению ромба, а также по третьему признаку. Если AW = CW, то BW является его медианной. В равнобедренном треугольнике она является биссектрисой, а также высотой. Последняя — проходит под прямым углом к противолежащей стороне. Следовательно, перпендикулярность двух диагоналей доказана.
В треугольнике ABC отрезок BW — биссектриса угла B. Аналогично необходимо доказывать для углов A, С и D (рассматриваются треугольники BAD, BCD и ADC соответственно). Таким методом доказано и второе свойство ромба. Однако для решения задач недостаточно признаков и свойств. Для этих целей необходимо использовать формулы.
Формулы для вычислений
Каждую геометрическую характеристику ромба можно определить, используя некоторые соотношения. В задачах бывают известны определенные значения. Однако их бывает недостаточно, поскольку для вычисления какого-либо параметра следует найти промежуточные величины.
Чтобы правильно понимать формулы, следует ввести некоторые обозначения. Они позволят заметно сократить записи. Этот особый подход часто применяют математики. Пусть дан ромб, который имеет такие параметры:
Кроме того, у него есть такие характеристики, как площадь (размерность) и периметр. Они обозначаются литерами S и P соответственно.
Периметр и размерность
Периметром геометрической фигуры называется величина, которая эквивалентна суммарному значению всех его сторон. Площадь — характеристика геометрического тела, которая показывает его размерность. Следует отметить, что размерность существует только у двумерной фигуры. Если последняя принадлежит трехмерному пространству, то необходимо вычислять ее объем, поскольку размерности у нее нет.
Для определения периметра существует одна формула P = 4a. Однако сторону можно выражать через S, R, D, d1, d2, высоту h, а также через углы f и g. Для S существует больше соотношений. Некоторые из них можно также дополнительно вывести, выражая через некоторые параметры. Базовыми формулами являются следующие:
В последнее соотношение необходимо верно подставлять значения. Нужно обратить внимание на то, что берется произведение большей диагонали d1 на тангенс острого угла g, и наоборот — значение меньшей диагонали, умноженной на тангенс тупого угла g.
Длина стороны
В задачах определенного типа возникает необходимость найти длину стороны. Для нахождения этого параметра ромба существуют также формулы и соотношения, которые помогут получить верный ответ. К базовым из них можно отнести следующие:
Чтобы вычисления были верными, необходимо учитывать, что в 5 и 6 пунктах угол f — острый, a g — тупой. Функция «sqrt» применяется в различных математических пакетах и языках программирования. Она эквивалентна квадратному корню из числа, которое находится под корнем.
Соотношения для диагоналей
Существуют определенные задачи, в которых необходимо найти диагонали ромба. Можно, конечно, не пользоваться готовыми формулами, а выводить их. Математики рекомендуют осуществлять такие операции, поскольку идет тренировка мозга. Однако в некоторых ситуациях, например на контрольной или экзамене, время не хватает. Следовательно, на решение нужно тратить меньше времени.
Как бы быстро ни считал человек в уме или пользовался калькулятором, лишние вычисления занимают много времени. Следовательно, для оптимизации нужно пользоваться готовыми соотношениями, позволяющими находить нестандартные параметры. К ним можно отнести вычисление длины диагоналей ромба (d1 — большая, d2 — меньшая). Для этого следует применять такие формулы:
В 11 и 12 формулах следует обратить особое внимание на обозначения углов. Острый угол — f, а тупой — g. Следует отметить, что все 12 пунктов — базовые формулы для нахождения диагоналей. Однако можно выводить соотношения самостоятельно, как в пунктах 5 и 6 (замена a 2 на S).
Вписанная окружность
Когда в ромб вписана окружность, то появляются другие соотношения. Очень часто математики специально вписывают ее, поскольку в результате такой операции открывается больше возможностей. Базовые соотношения следующие:
Необходимо отметить, что R = D / 2. Если умножить каждое из соотношений на 2, то можно получить значение диаметра D вписанной окружности.
Таким образом, очень важным шагом при решении задачи является идентификация геометрической фигуры. После этого можно применять основные формулы для нахождения неизвестных величин.
Параллелограмм: свойства и признаки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.