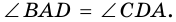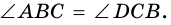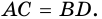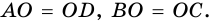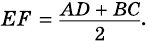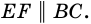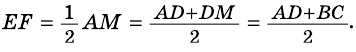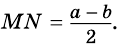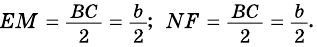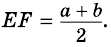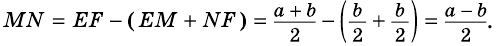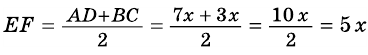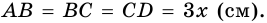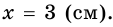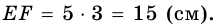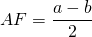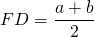Как доказать что диагонали трапеции равны
Как доказать что диагонали трапеции равны
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
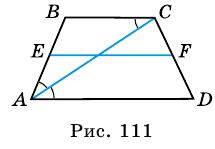
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
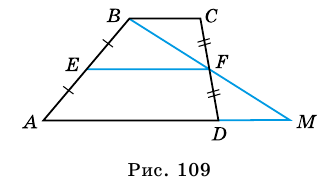
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
Трапеция и ее свойства с определением и примерами решения
Содержание:
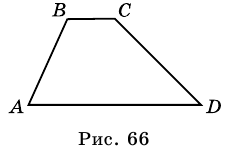
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 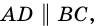
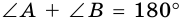
2. Трапеция является выпуклым четырехугольником.
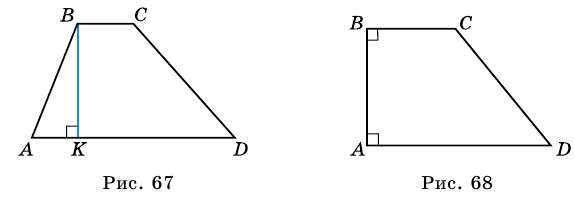
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 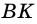
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
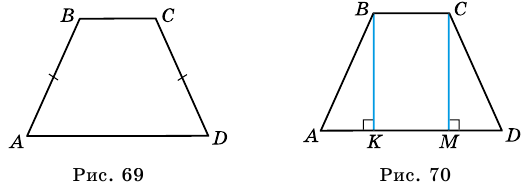
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 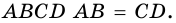
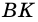
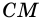
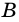
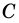
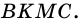
2) 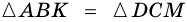
3) Также 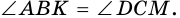
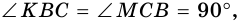
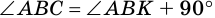
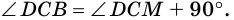
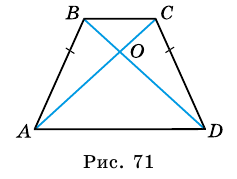
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 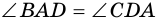
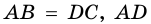
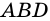
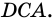
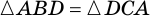
Пример:
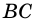
Доказательство:
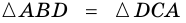
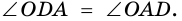
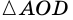
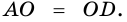
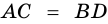
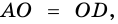
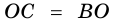
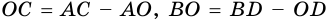
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 
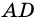
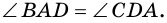
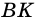
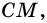
2) Тогда 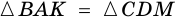
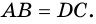
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 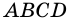
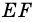
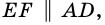
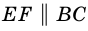
1) Проведем луч 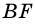
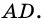
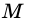
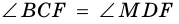
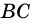
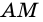
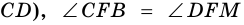
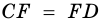
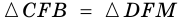
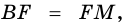
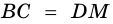
2) Поскольку 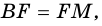
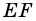
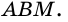
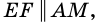
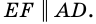
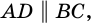
3) Кроме того,
Пример:
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 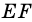
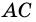
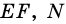
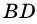
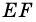
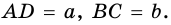
1) Так как 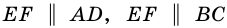
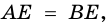
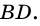
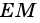
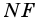
Тогда
2) 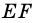
3)
Пример:
Решение:
Пусть 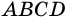
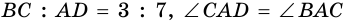
1) Обозначим 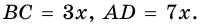
2) 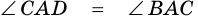
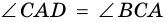
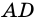
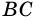
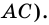
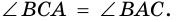
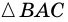
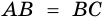
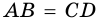
3) Учитывая, что 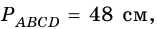
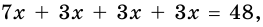
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Равнобедренная трапеция
Что такое равнобедренная трапеция и каковы ее свойства?
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Еще равнобедренную трапецию называют равнобокой (или равнобочной) трапецией.
ABCD — равнобедренная трапеция.
AD и BC — основания трапеции,
AB и CD — её боковые стороны,
Перечислим основные свойства равнобедренной трапеции.
Свойства равнобедренной трапеции:

2) Сумма противолежащих углов равнобедренной трапеции равна 180º.

4) Около любой равнобедренной трапеции можно описать окружность.
Кроме основных, у равнобедренной трапеции есть и другие свойства. Например, можно доказать один раз и в дальнейшем использовать при решении задач следующее утверждение:
Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

Признаки равнобедренной трапеции:
1) Если углы при основании трапеции равны, то она — равнобедренная.
2) Если сумма противолежащих углов трапеции равна 180º, то она — равнобедренная.
3) Если диагонали трапеции равны, то она — равнобедренная.
4) Если около трапеции можно описать окружность, то она — равнобедренная.