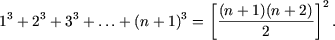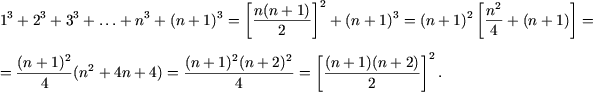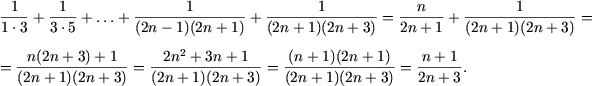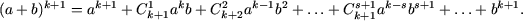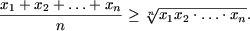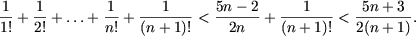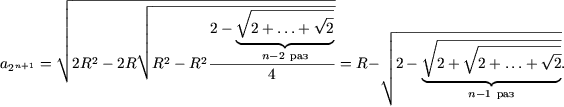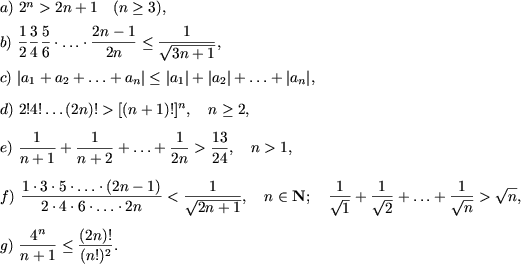Как доказать что для любого натурального n верно равенство
Как доказать что для любого натурального n верно равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 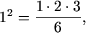
d) При n = 1 равенство справедливо: 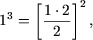
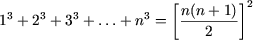
e) Утверждение P(1) справедливо: 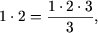
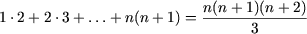
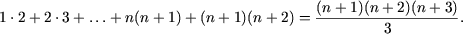
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 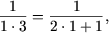
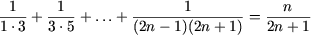
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
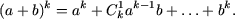
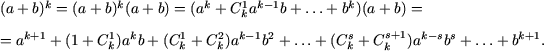
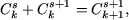
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
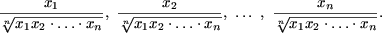
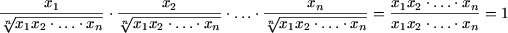
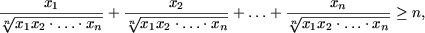
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 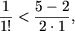
Допустим, что 
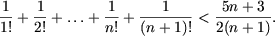
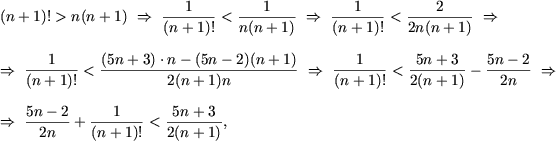
Поскольку при n > 10 имеем 
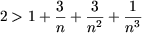
Пример 3. Доказать, что для любого n О N

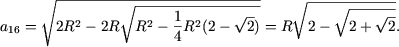
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 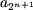
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
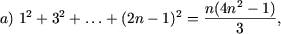 |
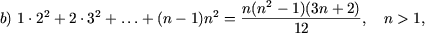 |
 |
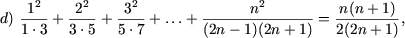 |
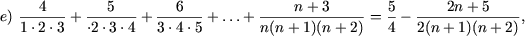 |
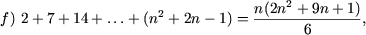 |
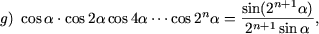 |
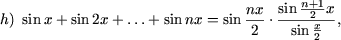 |
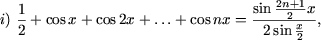 |
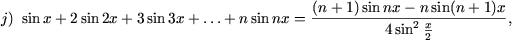 |
 |
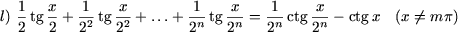 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 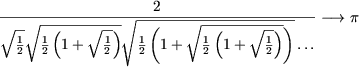
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.
Как доказать что для любого натурального n верно равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Как доказать что для любого натурального n верно равенство
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Автор работы награжден дипломом победителя II степени
Введение
Данная тема является актуальной, так как каждый день люди решают различные задачи, в которых они применяют разные методы решения, но есть задания, в которых не обойтись без метода математической индукции, и в таких случаях будут очень полезны знания в данной области.
Я выбрал данную тему для исследования, потому что в школьной программе методу математической индукции уделяют мало времени, ученик узнает поверхностнуюинформацию, которая поможетему получить лишь общее представление о данном методе, но чтобы углубленно изучить эту теорию потребуется саморазвитие. Действительно будет полезно поподробнее узнать о данной теме, так как это расширяет кругозор человека и помогает в решении сложных задач.
Цель работы:
Познакомиться с методом математической индукции, систематизировать знания по данной теме и применить её при решении математических задач и доказательстве теорем, обосновать и наглядно показать практическое значение метода математической индукции как необходимого фактора для решения задач.
Задачи работы:
Проанализировать литературу и обобщить знания по данной теме.
Разобраться в принципе метода математической индукции.
Исследовать применение метода математической индукции к решению задач.
Сформулировать выводы и умозаключения по проделанной работе.
Основная часть исследования
История возникновения:
Только к концу XIX века сложился стандарт требований к логической строгости, остающейся и до настоящего времени господствующими в практической работе математиков над развитием отдельных математических теорий.
Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида. Современное название метода было введено де Морганом в 1838 году.
Метод математической индукции можно сравнить с прогрессом: мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению логически развивать свою мысль, а значит, сама природа предначертала ему размышлять индуктивно.
Индукция и дедукция
Известно, что существуют как частные, так и общие утверждения, и на переходе от одних к другим и основаны два данных термина.
Дедукция (от лат. deductio – выведение) – переход в процессе познания от общего знания к частному и единичному. В дедукции общее знание служит исходным пунктом рассуждения, и это общее знание предполагается «готовым», существующим. Особенность дедукции состоит в том, что истинность ее посылок гарантирует истинность заключения. Поэтому дедукция обладает огромной силой убеждения и широко применяется не только для доказательства теорем в математике, но и всюду, где необходимы достоверные знания.
Индукция (от лат. inductio – наведение) – это переход в процессе познания от частного знания к общему.Другими словами, – это метод исследования, познания, связанный с обобщением результатов наблюдений и экспериментов.Особенностью индукции является ее вероятностный характер, т.е. при истинности исходных посылок заключение индукции только вероятно истинно и в конечном результате может оказаться как истинным, так и ложным.
Полная и неполная индукция
Индуктивное умозаключение – такая форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общности к знанию большей степени общности, а заключение, вытекающее из посылок, носит преимущественно вероятностный характер.
В ходе исследования я выяснил, что индукция делится на два вида: полная и неполная.
Полной индукцией называется умозаключение, в котором общий вывод о классе предметов делается на основании изучения всех предметов этого класса.
Например,пусть требуется установить, что каждое натуральное чётное число n в пределах 6≤ n≤ 18 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:
6=3+3; 8=5+3; 10=7+3; 12=7+5;14=7+7; 16=11+5; 18=13+5;
Данные равенства показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Рассмотрим следующий пример: последовательность yn= n 2 +n+17; Выпишем первые четыре члена: у1=19; y2=23; y3=29; y4=37; Тогда мы можем предположить, что вся последовательность состоит из простых чисел. Но это не так, возьмем y16= 16 2 +16+17=16(16+1)+17=17*17. Это составное число, значит наше предположение неверно, таким образом, неполная индукция не приводит к вполне надежным выводам, но позволяет сформулировать гипотезу, которая в дальнейшем требует математического доказательства или опровержения.
Метод математической индукции
Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для всех этих ситуаций мы не в состоянии.Но как осуществить проверку бесконечного числа случаев? Такой способ предложили Б.Паскаль и Я.Бернулли, это метод математической индукции, в основе которого лежит принцип математической индукции.
Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n>p, где p-фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом:
Если предложение А(n) истинно при n=p и если А(k) А(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.
Алгоритм (он состоит из четырех этапов):
1.база ( показываем, что доказываемое утверждение верно для некоторых простейших частных случаев ( п= 1));
2.предположение (предполагаем, что утверждение доказано для первых к случаев); 3.шаг ( в этом предположении доказываем утверждение для случая п= к + 1); 4.вывод ( утверждение верно для всех случаев, то есть для всех п).
Заметим, что Методом математической индукции можно решать не все задачи, а только задачи, параметризованные некоторой переменной. Эта переменная называется переменной индукции.
Применение метода математической индукции
Применим всю данную теорию на практике и выясним, в каких задачах применяется данный метод.
Задачи на доказательство неравенств.
Пример 1.Доказать неравенство Бернулли(1+х)n≥1+n х, х>-1, n € N.
Докажем с помощью метода математической индукции.
1) При n=1 неравенство справедливо, так как 1+х≥1+х
2) Предположим, что неравенство верно для некоторого n=k, т.е.
Умножив обе части неравенства на положительное число 1+х, получим
(1+x) k+1 ≥(1+kx)(1+ x) =1+(k+1) x + kx 2
Учитывая, что kx 2 ≥0, приходим к неравенству
Таким образом, из допущения, что неравенство Бернулли верно для n=k, следует, что оно верно для n=k+1. На основании метода математической индукции можно утверждать, что неравенство Бернулли справедливо для любого n € N.
Докажем с помощью метода математической индукции.
Обозначим левую часть неравенства через.
1), следовательно, при n=2 неравенство справедливо.
Задачи на доказательство тождеств.
Пример 1. Доказать, что для любого натурального n справедливо равенство:
1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.
Пусть n=1, тогда Х1=1 3 =1 2 (1+1) 2 /4=1.
Мы видим, что при n=1 утверждение верно.
2) Предположим, что равенство верно при n=kXk=k 2 (k+1) 2 /4.
3) Докажем истинность этого утверждения для n=k+1, т.е.Xk+1=(k+1) 2 (k+2) 2 /4. Xk+1=1 3 +2 3 +…+k 3 +(k+1) 3 =k 2 (k+1) 2 /4+(k+1) 3 =(k 2 (k+1) 2 +4(k+1) 3 )/4=(k+1) 2 (k 2 +4k+4)/4=(k+1) 2 (k+2) 2 /4.
Из приведённого доказательства видно, что утверждение верно при n=k+1, следовательно, равенство верно при любом натуральном n.
Пример 2. Доказать, что при любом натуральном nсправедливо равенство
2) Пусть тождество верно и для n = k, т.е..
3)Докажем, что это тождество верно и для n = k + 1, т.е.;
Т.к. равенство верно при n=kи n=k+1, то оно справедливо при любом натуральном n.
Задачи на суммирование.
2) Докажем, что А(k) A(k+1).
Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что
Итак, А(k) А(k+1). На основании принципа математической индукции заключаем, что предположение А(n) истинно для любого n N.
Пример 2. Доказать формулу, n – натуральное число.
Решение: При n=1 обе части равенства обращаются в единицу и, следовательно, первое условие принципа математической индукции выполнено.
Прибавим к обеим частям этого равенства и преобразуем правую часть. Тогда получим
Таким образом, из того, что формула верна при n=k, следует, что она верна и при n=k+1, то это утверждение справедливо при любом натуральном n.
Задачи на делимость.
Пример 1. Доказать, что (11 n+2 +12 2n+1 ) делится на 133 без остатка.
Решение: 1) Пусть n=1, тогда
(23× 133) делится на 133 без остатка, значит при n=1 утверждение верно;
2) Предположим, что (11 k+2 +12 2k+1 ) делится на 133 без остатка.
3) Докажем, что в таком случае
(11 k+3 +12 2k+3 ) делится на 133 без остатка. Действительно, 11 k+3 +12 2л+3 =11×11 k+2 +
Полученная сумма делится на 133 без остатка, так как первое её слагаемое делится на 133 без остатка по предположению, а во втором одним из множителей является 133.
Итак, А(k)→ А(k+1), то опираясь на метод математической индукции, утверждение верно для любых натуральных n.
Пример 2. Доказать, что 3 3n-1 +2 4n-3 при произвольном натуральном n делится на 11.
Решение: 1) Пусть n=1, тогдаХ1=3 3-1 +2 4-3 =3 2 +2 1 =11 делится на 11 без остатка. Значит, при n=1 утверждение верно.
2) Предположим, что при n=k
Xk=3 3k-1 +2 4k-3 делится на 11 без остатка.
3) Докажем, что утверждение верно для n=k+1.
Xk+1=3 3(k+1)-1 +2 4(k+1)-3 =3 3k+2 +2 4k+1 =3 3 *3 3k-1 +2 4 *2 4k-3 =
=27 3 3k-1 +16* 2 4k-3 =(16+11)* 3 3k-1 +16* 2 4k-3 =16* 3 3k-1 +
Первое слагаемое делится на 11 без остатка, поскольку 3 3k-1 +2 4k-3 делится на 11 по предположению, второе делится на 11, потому что одним из его множителей есть число 11. Значит и сумма делится на 11 без остатка при любом натуральном n.
Задачи из реальной жизни.
Пример 1. Доказать, что сумма Sn внутренних углов любого выпуклого многоугольника равна (п— 2)π, где п — число сторон этого многоугольника:Sn = (п— 2)π (1).
Это утверждение имеет смысл не для всех натуральных п, а лишь для п > 3, так как минимальное число углов в треугольнике равно 3.
1) При п = 3 наше утверждение принимает вид: S3 = π. Но сумма внутренних углов любого треугольника действительно равна π. Поэтому при п = 3 формула (1) верна.
Итак, оба условия принципа математической индукции выполняются, и потому формула (1) верна при любом натуральном п > 3.
Пример 2.Имеется лестница, все ступени которой одинаковы. Требуется указать минимальное число положений, которые гарантировали бы возможность «забраться» на любую по номеру ступеньку.
Все согласны с тем, что должно быть условие. Мы должны уметь забраться на первую ступень. Далее должны уметь с 1-ой ступеньки забраться на вторую. Потом во второй – на третью и т.д. на n-ую ступеньку. Конечно, в совокупности же «n» утверждений гарантирует нм то, что мы сможем добраться до n-ой ступеньки.
Посмотрим теперь на 2, 3,…., n положение и сравним их друг с другом. Легко заметить, что все они имеют одну и ту же структуру: если мы добрались до k ступеньки, то можем забраться на (k+1) ступеньку. Отсюда становится естественной такая аксиома для справедливости утверждений, зависящих от «n»: если предложение А(n), в котором n – натуральное число, выполняется при n=1 и из того, что оно выполняется при n=k (где k – любое натуральное число), следует, что оно выполняется и для n=k+1, то предположение А(n) выполняется для любого натурального числа n.
Приложение
Задачи с применением метода математической индукции при поступлении в ВУЗы.
Заметим, что при поступление в высшие учебные заведения также встречаются задачи, которые решаются данным методом. Рассмотрим их на конкретных примерах.
Пример 1.Доказать, что любом натуральном п справедливо равенство
1) При п=1 мы получаем верное равенство Sin.
2) Сделав предположение индукции, что при n=k равенство верно, рассмотрим сумму, стоящую в левой части равенства, при n=k+1;
3) Используя формулы приведения преобразуем выражение:
Тогда, в силу метода математической индукции равенство верно для любого натурального n.
Пример 2.Доказать, что для любого натурального n значение выражения 4n +15n-1 кратно 9.
2) Пусть равенство выполняется для n=k: 4 k +15k-1 кратно 9.
3) Докажем, что равенство выполняется и для следующего числа n=k+1
4 k+1 +15(k+1)-1=4 k+1 +15k+15-1=4•4 k +60k-4-45k+18=4(4 k +15k-1)-9(5k-2)
Следовательно и все выражение 4(4 k +15k-1)-9(5k-2) кратно 9, что и требовалось доказать.
Пример 3. Доказать, что при любом натуральном числе п выполняется условие : 1∙2∙3+2∙3∙4+…+ п(п+1)(п+2)=.
1) Проверим, что данная формула верна при п=1: Левая часть = 1∙2∙3=6.
2) Предположим, что данная формула верна при n=k:
3) Докажем, что данная формула верна при n=k+1:
Итак, данное условие верно в двух случаях и доказали, что верно при n=k+1, следовательно она верно при любом натуральном числе п.
Заключение
Подведем итоги, в процессе исследования я выяснил, в чем заключается индукция, которая бывает полной или неполной, познакомился с методом математической индукции, основанном на принципе математической индукции, рассмотрел множество задач с применением данного метода.
Также я узнал много новой информации, отличной от той, что включена в школьную программу.Изучая метод математической индукции я использовал различную литературу, ресурсы интернета, а также консультировался с педагогом.
Вывод: Обобщив и систематизировав знания по математической индукции, убедился в необходимости знаний по данной теме в реальной действительности. Положительным качеством метода математической индукции является его широкое применение в решении задач: в области алгебры, геометрии и реальной математики. Также эти знания повышают интерес к математике, как к науке.
Я уверен, что навыки, приобретенные в ходе работы, помогут мне в будущем.
Список литературы
Соминский И.С. Метод математической индукции. Популярные лекции по математике, выпуск 3-М.: Наука, 1974г.
Л. И. Головина, И. М. Яглом. Индукция в геометрии. — Физматгиз, 1961. — Т. 21. — 100 с. — (Популярные лекции по математике).
Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих в вузы (Избранные вопросы элементарной математики) – Изд.5-е, перераб., 1976 – 638с.
А. Шень. Математическая индукция. — МЦНМО, 2004. — 36 с.
M.Л.Галицкий, А.М.Гольдман, Л.И.Звавич Сборник задач по алгебре: учеб.пособие для 8-9 кл. с углубл. изучением математики 7-е изд.— М.: Просвещение, 2001.—271 с
Макарычев Ю.Н., Миндюк Н.Г Дополнительные главы к школьному учебнику алгебры 9 класса. – М.: Просвещение, 2002.