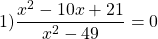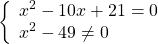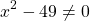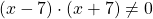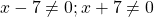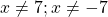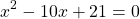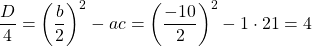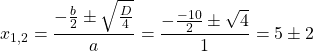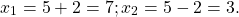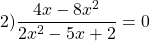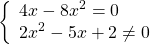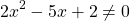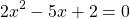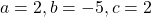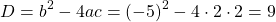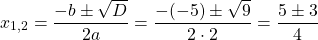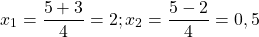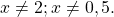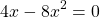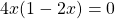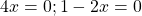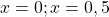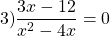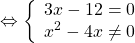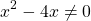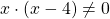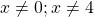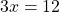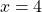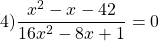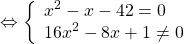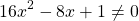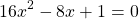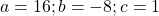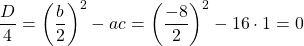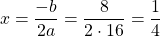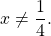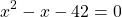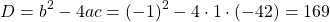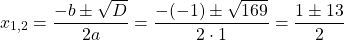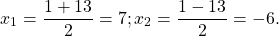Как доказать что дробь равна нулю

Дробь равна нулю

Когда дробь равна нулю?

Дробная черта — это знак деления. При делении нуля на любое число, кроме нуля, получим нуль. На нуль делить нельзя.

Таким образом, дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля.

Решение многих задач в алгебре сводится к решению дробно рациональных уравнений, которые, в свою очередь, сводятся к уравнению типа «дробь равна нулю».

Схематически решение уравнения типа «дробь равна нулю» можно изобразить так:

Таким образом, чтобы решить уравнение типа «дробь равна нулю», надо:

1) Найти значения переменной, при которых знаменатель обращается в нуль.

2) Приравнять к нулю числитель и решить получившееся уравнение.

3) Проверить, нет ли среди корней уравнения «числитель равен нулю» значений, при которых знаменатель обращается в нуль. Если есть, их следует исключить.

Дробь равна нулю, если числитель равен нулю, а знаменатель — отличен от нуля, поэтому это уравнение равносильно системе

Находим значения переменной, при которых знаменатель обращается в нуль:

Можно приравнять выражение, стоящее в левой части неравенства, к нулю, и решать как обычное неполное квадратное уравнение. Можно решать как уравнение, только вместо знака равенства каждый раз писать «≠».

При этих значениях переменной выражение, стоящее в левой части уравнения, не имеет смысла (так как на нуль делить нельзя).

Решаем уравнение, в котором числитель равен нулю.

Так как D/4>0, уравнение имеет два корня:

Первый из корней — посторонний (он не удовлетворяет условию x≠7), поэтому в ответ записывает только корень 3. Ответ: 3.

Это уравнение равносильно системе

Его корни — значения переменной, при котором выражение, стоящее в левой части уравнения, не имеет смысла.

Общий множитель 4x выносим за скобки

Второй корень не подходит (он не удовлетворяет условию x≠0,5).

Переходим к решению уравнения 3x-12=0. Это — линейное уравнение. Неизвестное — в одну сторону, известное — в другую с противоположным знаком:

Полученный корень является посторонним, так как не удовлетворяет условию x≠4. Значит, исходное уравнение типа «дробь равна 0» корней не имеет.

Решаем квадратное уравнение

Так как D/4=0, квадратное уравнение имеет один корень

Теперь решаем уравнение

Посторонних корней нет (оба корня удовлетворяют условию x≠1/4).

Источник

Решение уравнений «дробь равна нулю», описание метода, примеры

В чем состоит метод решения и на чем он базируется?

Базируется метод на следующем утверждении:

Докажем это утверждение в следующем пункте.

Обоснование метода

Начнем с доказательства частных случаев.

Первая часть доказана. Приступаем к доказательству второй части.

Так доказана вторая часть и все утверждение в целом.

Алгоритм решения уравнений «дробь равна нулю»

Доказанное утверждение позволяет записать алгоритм решения уравнений «дробь равна нулю»:

Решение примеров

Рассмотрим решения трех характерных уравнений «дробь равна нулю»: с нулем в числителе, с отличным от нуля числом в числителе, и с выражением с переменной в числителе. Ими мы закроем все три типичные ситуации.

Сначала решим уравнение с нулем в числителе: .

Решите уравнение

Теперь решим уравнение , в числителе которого отличное от нуля число.

Решите уравнение

Осталось рассмотреть решение уравнения «дробь равна нулю» в случае, когда в числителе находится выражение с переменной, а не число. В этом случае, согласно алгоритму, нужно приравнять к нулю числитель, решить полученное уравнение и отсеять посторонние корни.

Решите уравнение

Источник

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

– числитель, знаменатель обыкновенной дроби;

– сократимая, несократимая дробь;

– основное свойство дроби.

Дробь в математике – это число, состоящее из одной или нескольких равных частей (долей) единицы.

Правильные дроби – это дроби, в которых числитель меньше знаменателя.

Несократимая дробь – это дробь, в которой числитель и знаменатель являются взаимно простыми числами (имеют только один общий делитель – 1).

Сократимая дробь – это дробь, у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице.

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

«Все, что без этого было темно, сомнительно и неверно, математика сделала ясным, верным и очевидным», – сказал Михаил Васильевич Ломоносов.

Эти слова как нельзя кстати походят к теме нашего занятия, на котором мы будем устанавливать между, казалось бы, разными дробями равенство, хоть и не вполне очевидное с первого взгляда.

Итак, выясним, какие дроби можно назвать равными.

Для начала нарисуем отрезок. Далее разделим его на две части. Затем каждую из половинок разделим ещё на две части.

Получается, что весь отрезок поделён на четыре части. Если теперь сложить две части из четырёх, то получится ровно половина отрезка, которая в виде обыкновенной дроби будет записана как одна вторая.

Получается, что одна вторая это тоже самое, что и две четвёртых, т. е. это равные дроби.

Возьмём торт и разделим его на 10 частей.

Половина торта – это 5 частей. В виде обыкновенной дроби получается, что частям торта. Отсюда получается так называемое основное свойство дроби, которое заключается в следующем: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

С помощью этого свойства всегда получаются равные дроби. Например,

Аналогично, представим семь в виде дроби:

Если возьмём число один, представим его в виде дроби, то получим:

Получается, что две равные дроби являются различными записями одного и того же числа.

Это свойство можно применить и в обратном порядке, в этом случае говорят, что дробь можно сократить. Если числитель и знаменатель дроби имеют общий множитель, то дробь можно сократить на этот множитель, т. е. разделить на него числитель и знаменатель.

В этом случае тоже получается равная дробь. Такие дроби называются сократимыми.

Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице. Например,

Рассмотрим ещё один пример, возьмём дробь :

Стоит отметить, что общий множитель числителя и знаменателя можно найти как их НОД. Например,

Стоит отметить, что сокращать дроби можно постепенно, эти действия всё равно приведут к нужному результату.

Но дроби не всегда можно сократить.

Если числитель и знаменатель дроби являются взаимно простыми числами (имеют только один общий делитель – 1), то такая дробь называется несократимой.

Например, ; – несократимые дроби.

Решим задание, связанное с сокращением дробей.

Укажите все общие делители, НОД числителя и знаменателя дроби и сократите дробь.

Решение: начнём с того, что определим общие делители числителя и знаменателя дроби, разложив их на множители:

Источник