Как доказать что две плоскости перпендикулярны

Перпендикулярные плоскости, условие перпендикулярности плоскостей.

Эта статья о перпендикулярных плоскостях. Сначала дано определение перпендикулярных плоскостей, показаны обозначения и приведены примеры. После этого сформулирован признак перпендикулярности плоскостей и условие перпендикулярности двух плоскостей. В заключении детально разобраны решения характерных задач.

Навигация по странице.

Перпендикулярные плоскости – основные сведения.

Определение перпендикулярных плоскостей дается через угол между пересекающимися плоскостями.

Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен девяноста градусам.

Для обозначения перпендикулярности используют символ вида «». То есть, если плоскости и перпендикулярны, то можно кратко записать .

Если плоскости и перпендикулярны, то можно также сказать, что плоскость перпендикулярна к плоскости или плоскость перпендикулярна к плоскости . Поэтому перпендикулярные плоскости и часто называют взаимно перпендикулярными.

В качестве примера перпендикулярных плоскостей можно привести плоскости стены и пола в комнате.

Перпендикулярность плоскостей – признак и условие перпендикулярности.

На практике часто приходится определять, перпендикулярны ли две заданные плоскости. Для этого можно найти угол между заданными плоскостями, и если он будет равен , то по определению плоскости будут перпендикулярными.

Также существует признак перпендикулярности двух плоскостей, который часто используется для доказательства перпендикулярности двух плоскостей. В его формулировке участвуют перпендикулярные прямая и плоскость. Сформулируем признак перпендикулярности двух плоскостей в виде теоремы.

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.

Из этого признака напрямую следует, что если плоскость перпендикулярна к линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Теперь рассмотрим необходимое и достаточное условие перпендикулярности двух плоскостей, которое удобно применять для проверки перпендикулярности плоскостей, заданных в прямоугольной системе координат в трехмерном пространстве. Определение нормального вектора плоскости позволяет доказать следующее необходимое и достаточное условие перпендикулярности двух плоскостей.

Для перпендикулярности двух пересекающихся плоскостей необходимо и достаточно, чтобы нормальные векторы этих плоскостей были перпендикулярны.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат. Если и — нормальные векторы плоскостей и соответственно, то необходимое и достаточное условие перпендикулярности векторов и имеет вид . Таким образом, если и — нормальные векторы плоскостей и соответственно, то для перпендикулярности плоскостей и необходимо и достаточно, чтобы скалярное произведение векторов и равнялось нулю, то есть, чтобы выполнялось равенство .

Разберем решения нескольких примеров.

Перпендикулярны ли плоскости, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?

Чтобы ответить на вопрос о перпендикулярности заданных плоскостей, найдем координаты нормальных векторов этих плоскостей и проверим выполнение условия перпендикулярности этих векторв.

Общее уравнение плоскости позволяет сразу записать координаты нормального вектора: .

Чтобы определить координаты нормального вектора плоскости , перейдем от уравнения плоскости в отрезках к общему уравнению плоскости: . Таким образом, — нормальный вектор плоскости .

Вычислим скалярное произведение векторов и : . Так как оно отлично от нуля, то векторы и не перпендикулярны, следовательно, заданные плоскости не перпендикулярны.

нет, плоскости не перпендикулярны.

Убедимся, что скалярное произведение нормальных векторов указанных плоскостей равно нулю – это будет доказательством перпендикулярности плоскостей. Для этого сначала нам нужно найти координаты нормальных векторов и плоскостей АВС и ABD соответственно.

Нормальным вектором плоскости АВС является векторное произведение векторов и , а нормальным вектором плоскости ABD является векторное произведение векторов и , то есть,

Заметим, что можно было по координатам заданных точек получить общие уравнения плоскостей АВС и ABD (смотрите статью уравнение плоскости, проходящей через три заданные точки), из них найти координаты нормальных векторов этих плоскостей, после чего проверить выполнение условия перпендикулярности нормальных векторов плоскостей.

Источник

Перпендикулярные плоскости, условие перпендикулярности плоскостей

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Перпендикулярные плоскости – основные сведения

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.

Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Рассмотрим подробнее на примерах.

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Источник

Перпендикулярность плоскостей

Вы будете перенаправлены на Автор24

Понятие перпендикулярных плоскостей

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

Рисунок 1. Перпендикулярные плоскости

Признак перпендикулярности двух плоскостей

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Примеры задач

Решение.

Готовые работы на аналогичную тему

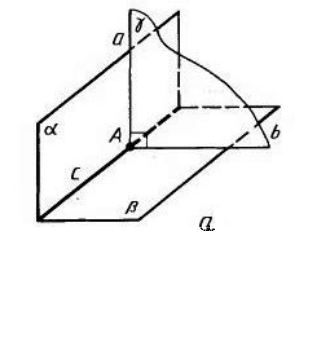
Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 04 2021

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №11. Перпендикулярность плоскостей

Перечень вопросов, рассматриваемых в теме.

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Перпендикуляры к ребру двугранного угла образуют линейный угол двугранного угла. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Если угол между пересекающимися плоскостями равен 90 градусом, то плоскости перпендикулярны.

Признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Следствие из признака перпендикулярности плоскостей: Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Прямоугольный параллелепипед – фигура, у которой все боковые ребра перпендикулярны основанию.

Атанасян Л.С., Бутузов В.Ф. Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.

Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а, которая является общей границей полуплоскостей, называется ребром двугранного угла (рис. 1а и 1б).

Двугранный угол с ребром CD, на разных гранях которого отмечены точки A и B называют двугранным углом CABD.

Перпендикуляры к ребру AO и BO образуют линейный угол двугранного угла AOB (рис. 1в). Так как луч ОА перпендикулярен прямой CD и луч OB перпендикулярен прямой CD, то плоскость АОВ перпендикулярна к прямой CD. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов

Градусной мерой двугранного угла называется градусная мера его линейного угла. Так же как и плоские углы, двугранные углы могут быть прямыми, острыми и тупыми.

Все линейные углы двугранного угла равны друг другу.

Рассмотрим два линейных угла АОВ и А₁О₁В₁ (рис. 1г). Лучи ОА и О₁А₁, лежат в одной грани и перпендикулярны к прямой ОО₁, поэтому они сонаправлены. Точно так же сонаправлены лучи OB и O₁B₁. Поэтому углы АОВ и А₁О₁В₁ равны как углы с сонаправленными сторонами.

Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

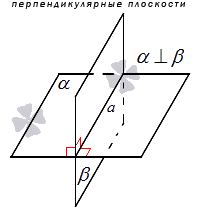
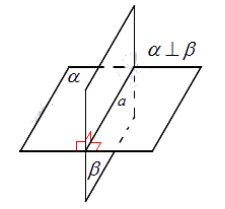
Если один из этих двугранных углов равен фи, то другие три угла равны соответственно 180 градусов минус фи, фи и 180 градусов минус фи (рис. 2 а). В частности, если один из углов прямой, то и остальные три угла прямые. Если угол между пересекающимися плоскостями равен 90 градусом, будем называть такие плоскости перпендикулярными (рис. 2б).

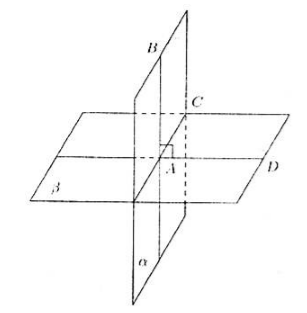
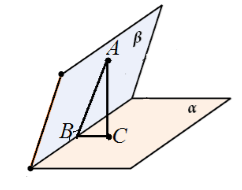
Для доказательства теоремы рассмотрим плоскости альфа и бетта такие (рис. 3), что плоскость альфа проходит через прямую АВ, перпендикулярную к плоскости бетта и пересекающуюся с ней в точке А. Докажем, что плоскости альфа и бетта перпендикулярны. Плоскости альфа и бетта пересекаются по некоторой прямой АС. При этом прямая АВ перпендикулярна прямой АС, так как по условию прямая АВ перпендикулярна плоскости бетта, это означает, что прямая АВ перпендикулярна к любой прямой, лежащей в плоскости бетта.

Проведем в плоскости бетта прямую AD, перпендикулярную к прямой АС. Тогда угол BAD — линейный угол двугранного угла, образованного при пересечении плоскостей альфа и бетта. Но угол BAD равен 90 градусов так как прямая АВ перпендикулярна плоскости бетта. Следовательно, угол между плоскостями альфа и бетта равен 90 градусов. Что и требовалось доказать.

Из этой теоремы вытекает важное следствие:

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

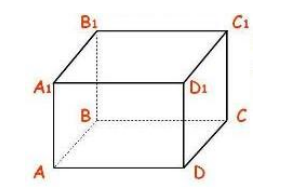
На рисунке 4 представлен прямоугольный параллелепипед. У этой фигуры все боковые ребра перпендикулярны основанию.

Его основаниями служат прямоугольники ABCD и A₁B₁C₁D₁, а боковые ребра АА₁,BB₁,CC₁ и DD₁ перпендикулярны к основаниям. Отсюда следует, что ребро АА₁ перпендикулярно к ребру АВ, т. е. боковая грань АА₁В₁В является прямоугольником. То же самое можно сказать и об остальных боковых гранях.

Таким образом, прямоугольный параллелепипед обладает следующими свойствами:

1) В прямоугольном параллелепипеде все шесть граней — прямоугольники.

2) Все двугранные углы прямоугольного параллелепипеда — прямые.

3) Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Измерениями прямоугольного параллелепипеда называются длины трех ребер, имеющих общую вершину.

Докажем последнее свойство.

Так как ребро СС₁ перпендикулярно к основанию ABCD, то угол АСС₁, прямой. Из прямоугольного треугольника АСС₁, по теореме Пифагора получаем

Следствием из этого свойства является то, что диагонали прямоугольного параллелепипеда равны.

Стоит отметить, что если у прямоугольного параллелепипеда все три измерения равны, то он называется, а все его грани являются равными друг другу квадратами.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ (рис. 5) боковая грань DD₁C₁C – квадрат, DC равно 4 см, BD₁ равно 6 см. Найдите BC и докажите, что плоскости BCD₁ и DC₁ B₁ взаимно перпендикулярны.

Сначала найдем BC. Воспользуемся тем свойством прямоугольного параллелепипеда, что квадрат его диагонали равен сумме квадратов трех его измерений.

Тогда диагональ BD₁ в квадрате равна AD в квадрате плюс DD₁ в квадрате плюс DC в квадрате. BD₁ – известно из условия, DD₁ и DC – стороны квадрата и тоже известны из условия, тогда отсюда мы можем выразить ребро AD, которое ребру BC.Отсюда находим, что BC равно 2 сантиметрам.

Для доказательства перпендикулярности плоскостей BCD₁ и DC₁ B₁ воспользуемся признаком перпендикулярности плоскостей. Этот признак звучит следующим образом: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Заметим, что плоскость BCD₁ проходит через диагональ грани DD₁ C₁C – CD₁. Эта диагональ перпендикулярна плоскости DC₁ B₁ в соответствии с признаком перпендикулярности прямой и плоскости, так как CD₁ перпендикулярна второй диагонали квадрата – C₁D и перпендикулярна ребру прямоугольного параллелепипеда C₁ B₁. Что и требовалось доказать.

Тестовый вопрос №2. В прямом двугранном угле дана точка A. Расстояния от точки A до граней угла: AA₁=6 см и AB₁=8 см. Определите расстояние от точки A до ребра двухгранного угла.

Отрезки AA₁ и AB₁ перпендикулярны граням двугранного угла, поэтому AA₁BB₁ – прямоугольник. Искомое расстояние – диагональ этого прямоугольника, которую найдем с помощью теоремы Пифагора: сантиметров.

Тестовый вопрос №10. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ длины рёбер: AB = 2, BC=3, AA₁ = 4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C_​1​​.

Решение. Нарисуем рисунок.

В рассматриваемом прямоугольном параллелепипеде проведем отрезок BC_​1​​. Затем построим плоскость на прямых BC_​1​​ и AB. Так как плоскости прямоугольного параллелепипеда AA₁D₁D и BB₁C₁C параллельны, поэтому искомым сечением является прямоугольник ABC₁D₁.

Источник