Как доказать что функции пересекаются в одной точке

Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.

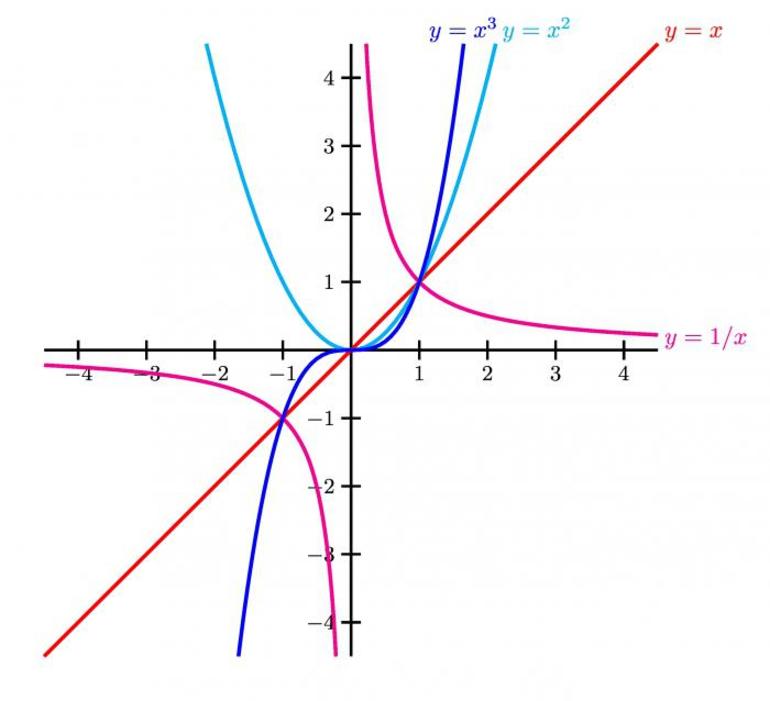
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.

Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.

Классификация уравнений

Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:

Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.

Математические преобразования

Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.

Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.

Разложение на множители

Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:

Методики нахождения точек

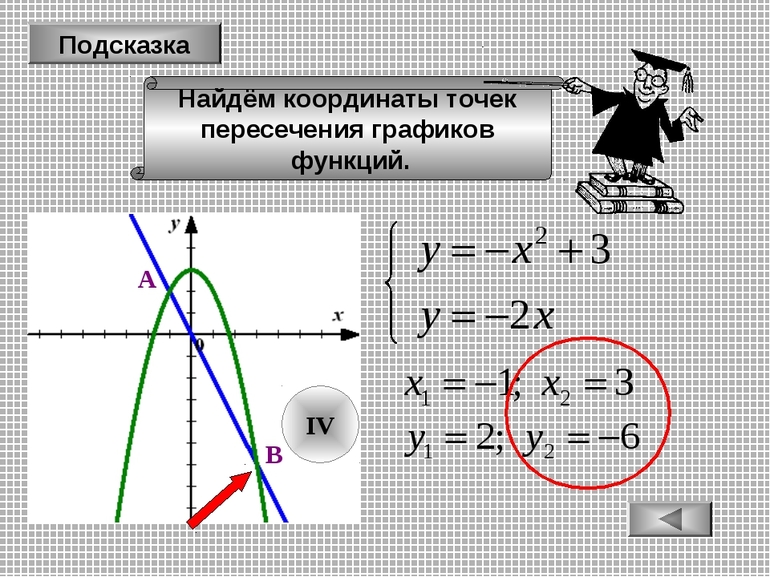
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.

Первой и второй степени

Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:

Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.

Пример решения

Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:

В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.

Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.

Источник

Пересекающиеся плоскости

Плоскость — это одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Линия пересечения двух плоскостей — это прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Содержание:

Понятие пересекающихся плоскостей

Определение. Плоскости, которые имеют хотя бы одну общую точку, называют пересекающимися.

Аксиома 5. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой . Плоскости и в этом случае являются пересекающимися по прямой (рис. 2.379).

Пример:

Дана плоскость . Доказать, что существует другая плоскость (3, пересекающая .

Решение:

Из условия задачи имеем:

1. Плоскость (дано) (рис. 2.380).

2. Нужно доказать, что существует другая плоскость , пересекающая .

Мы знаем, что на основании аксиомы 3 (аксиомы плоскости) три точки определяют единственную плоскость.

3. Возьмем точки А и В, принадлежащие плоскости , и точку С, не лежащую на прямой АВ и не принадлежащую (построение) (рис. 2.381).

4. Точки А, В и С не лежат на одной прямой. Через них можно провести плоскость , и притом только одну (3, аксиома 3).

5. Плоскости и имеют общую точку (1, 3, 4).

6. Плоскости и пересекаются по прямой АВ (5, аксиома 5) (рис. 2.382).

7. Мы доказали, что существует плоскость Р, пересекающая . (6)

Замечание. Если допустить, что точка С лежит на прямой АВ, то она будет лежать и в плоскости , что противоречит выбору точки С.

Двугранные углы

При пересечении плоскостей образуются двугранные углы.

Определение. Фигуру, образованную двумя полуплоскостями, исходящими из одной прямой, называют двугранным углом. Прямую называют ребром, а полуплоскости — сторонами или гранями двугранного угла.

На рисунке 2.383 изображен двугранный угол с ребром АВ.

Этот угол можно обозначать двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежит несколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, одна крайняя — у одной грани, другая — у другой (рис. 2.384).

Определение. Если через произвольную точку ребра двугранного угла провести плоскость, перпендикулярную ребру, то в пересечении этой плоскости с двугранным углом образуется угол, который называют линейным углом двугранного угла.

На рисунке 2.385 изображен линейный угол АОВ двугранного угла АОСВ. Вершиной линейного угла служит точка О, лежащая на ребре ос двугранного угла, а сторонами — лучи граней, исходящие из точки о и перпендикулярные ребру двугранного угла.

Двугранный угол имеет бесконечное множество линейных углов (рис. 2.386).

Определение. Градусной мерой двугранного угла называют градусную меру любого из его линейных углов.

Определение. Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).

Можно доказать следующее утверждение.

Теорема 1. Все линейные углы двугранного угла равны друг другу.

Для двугранных углов так же, как и для плоских, вводится понятие его градусной меры — величины.

Определение. Два двугранных угла называют равными, если они имеют одну и ту же градусную меру.

Если градусная мера одного из двугранных углов больше градусной меры другого, то говорят, что первый двугранный угол больше второго, а второй меньше первого. На рисунке 2.387 изображены три двугранных угла с общим ребром АВ. Двугранные углы CABD и DABE равны, так как их градусные меры равны 30°. Двугранный угол САВЕ больше двугранного угла CABD.

Подобно плоским углам, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

Все сказанное можно сформулировать в виде теорем.

Теорема 2. 1. Равным двугранным углам соответствуют равные линейные углы.

2. Большему двугранному углу соответствует больший линейный угол.

Верна и обратная теорема.

Теорема 3. 1. Равным линейным углам соответствуют равные двугранные углы.

2. Большему линейному углу соответствует больший двугранный угол.

Из теорем 2 и 3 легко получить три следствия.

Следствие 1. Прямому двугранному углу соответствует прямой линейный угол, и обратно.

Следствие 2. Все прямые двугранные углы равны, потому что у них равны линейные углы.

Следствие 3. Вертикальные двугранные углы равны.

Пример:

Из условия теоремы имеем:

1. PABQ и — два данных двугранных угла (рис. 2.388).

2. Вложим угол в угол АВ так, чтобы ребро совпало с ребром АВ, а грань — с гранью Р (построение) (рис. 2.389).

3. Если эти двугранные углы равны, то грань совпадает с Q; если же двугранные углы не равны, то грань займет некоторое положение, не совпадающее с Q, например положение (1, 2).

4. Возьмем на общем ребре какую-нибудь точку В и проведем через нее плоскость , перпендикулярную ребру АВ (построение) (рис. 2.390).

5. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы.

Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол cbd; если же двугранные углы не совпадут (если, например, грань займет положение то у большего двугранного угла окажется больший линейный угол (именно ) (3, 4).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник