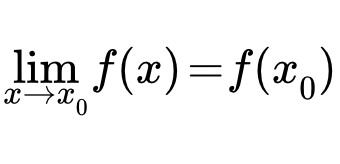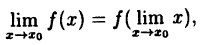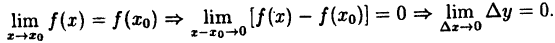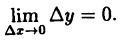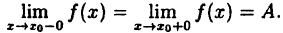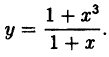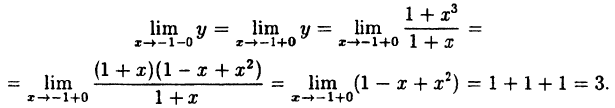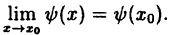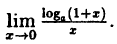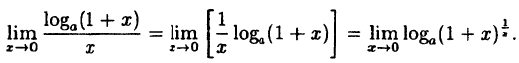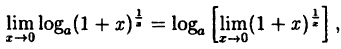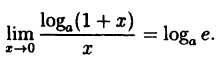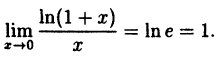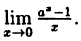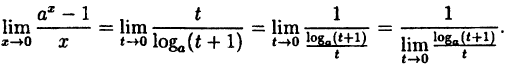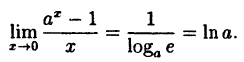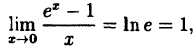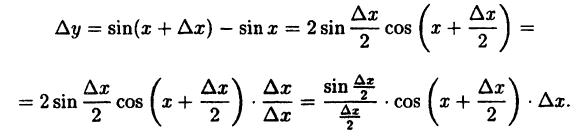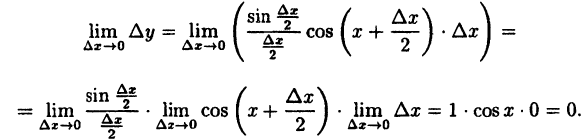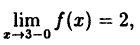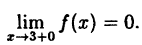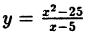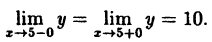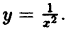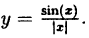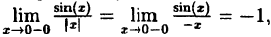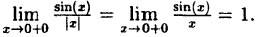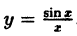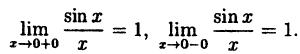Как доказать что функция непрерывна

Непрерывность функции в точке, разрывы первого и второго рода

Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.

Непрерывность функции в точке

Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.

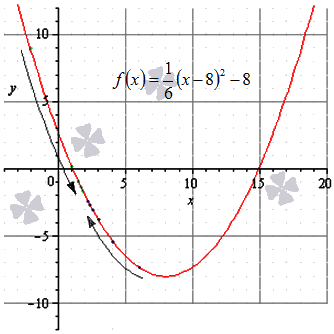
Решение

Соответствующая последовательность значений функций выглядит так:

на чертеже они обозначены зеленым цветом.

Соответствующая последовательность функций:

на рисунке обозначена синим цветом.

После вычисления значения функции в заданной точке очевидно выполнение равенства:

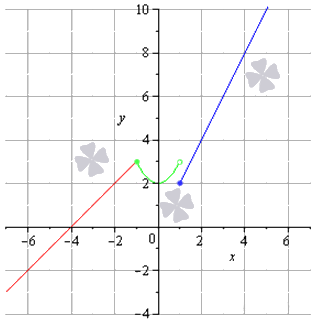
Устранимый разрыв первого рода

Решение

Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.

Неустранимый разрыв первого рода

Неустранимый разрыв первого рода также определяется точкой скачка функции.

Решение

Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:

Ответ: в конечном счете мы получили:

Нам остается только подготовить чертеж данного задания.

Разрыв второго рода (бесконечный разрыв)

Решение

Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:

Ей соответствует последовательность значений функции:

Источник

Непрерывность функции

Понятие непрерывности функции.

Функция \(f(x)\), определенная в некоторой окрестности точки \(a\), называется непрерывной в точке \(a\), если
$$
\displaystyle \lim_f(x)=f(a)\label
$$

Таким образом, функция \(f\) непрерывна в точке \(a\), если выполнены следующие условия:

Определение непрерывности функции \(f(x)\) в точке \(a\), выраженное условием \eqref, можно сформулировать с помощью неравенств (на языке \(\varepsilon-\delta\)), с помощью окрестностей и в терминах последовательностей соответственно в виде

Следует обратить внимание на то, что в определении непрерывности функции, в отличие от определения предела, рассматривается полная, а не проколотая окрестность точки \(a\), и пределом функции является значение этой функции в точке \(a\).

Назовем разность \(x-a\) приращением аргумента и обозначим \(\Delta x\), а разность \(f(x)-f(a)\) — приращением функции, соответствующим данному приращению аргумента \(\Delta x\), и обозначим \(\Delta y\). Таким образом,
$$
\Delta x=x-a,\;\Delta y=f(x)-f(a)=f(a+\Delta x)-f(a).\nonumber
$$

При этих обозначениях равенство \eqref примет вид
$$
\lim_<\Delta x\rightarrow 0>\Delta y=0.\nonumber
$$

Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Показать, что функция \(f(x)\) непрерывна в точке \(a\), если:

По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция \(f\) определена на полуинтервале \((a-\delta,a]\) и \(\displaystyle \lim_f(x)=f(a)\), то есть\(f(a-0)=f(a)\), то эту функцию называют непрерывной слева в точке \(a\).

Аналогично, если функция \(f\) определена на полуинтервале \([a,a+\delta)\) и \(f(a+0)=f(a)\), то эту функцию называют непрерывной справа в точке \(a\).

Например, функция \(f(x)=[x]\) непрерывна справа в точке \(x=1\) и не является непрерывной слева в этой точке, так как \(f(1-0)=0,\;f(1+0)=f(1)=1\).

Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке.

Точки разрыва.

Будем предполагать, что функция \(f\) определена в некоторой проколотой окрестности точки \(a\).

Точку \(a\) назовем точкой разрыва функции \(f\), если эта функция либо не определена в точке \(a\), либо определена, но не является непрерывной в точке \(a\).

Следовательно, \(a\) — точка разрыва функции \(f\), если не выполняется по крайней мере одно из следующих условий:

Если \(a\) — точка разрыва функции \(f\), причем в этой точке существуют конечные пределы слева и справа, то есть \(\displaystyle \lim_f(x)=f(a-0)\) и \(\displaystyle \lim_f(x)=f(a+0)\), то точку \(a\) называют точкой разрыва первого рода.

Если \(x=a\) — точка разрыва первого рода функции \(f(x)\), то разность \(f(a+0)-f(a-0)\) называют скачком функции в точке \(a\). В случае когда \(f(a+0)=f(a-0)\), точку \(a\) называют точкой устранимого разрыва. Полагая \(f(a)=f(a+0)=f(a-0)=A\), получим функцию
$$
f(x)=\left\<\beginf(x),\;если\;x\neq a,\\A,\;если\;x=a,\end\right.\nonumber
$$
непрерывную в точке \(a\) и совпадающую с \(f(x)\) при \(x\neq a\). В этом случае говорят, что функция доопределена до непрерывности в точке \(a\).

Пусть \(x=a\) — точка разрыва функции \(f\), не являющаяся точкой разрыва первого рода. Тогда ее называют точкой разрыва второго рода функции \(f\). В такой точке хотя бы один из односторонних пределов либо не существует, либо бесконечен.

Например, для функции \(f(x)=\displaystyle x\sin<\frac<1>>\) точка \(x=0\) — точка разрыва первого рода. Доопределив эту функцию по непрерывности, получим функцию
$$
\overline(x)=\left\<\begin
x\sin<\frac<1>>,\;если\;x\neq 0,\\
0,\;если\;x=0,
\end\right.\nonumber
$$
непрерывную в точке \(x=0\), так как
$$
\lim_x\sin\frac<1>=0.\nonumber
$$

Для функций \(\displaystyle \sin<\frac<1>>\) и \(\displaystyle \frac<1>\) точка \(x=0\) — точка разрыва второго рода.

Если функция \(f\) определена на отрезке \([a,b]\) и монотонна, то она может иметь внутри этого отрезка точки разрыва только первого рода.

\(\circ\) Пусть \(x_0\) — произвольная точка интервала \((a,b)\). Функция \(f\) имеет в точке \(x_<0>\) конечные пределы слева и справа. Если, например, \(f\) — возрастающая функция, то
$$
f(x_<0>-0)\leq f(x_<0>)\leq f(x_<0>+0),\nonumber
$$
где \(f(x_<0>-0)\) и \(f(x_<0>+0)\) — соответственно пределы функции \(f\) слева и справа в точке \(x_<0>\).

Свойства функций, непрерывных в точке.

Локальные свойства непрерывной функции.

Если функция \(f\) непрерывна в точке \(a\), то она ограничена в некоторой окрестности этой точки, то есть
$$
\exists\delta>0\quad\exists C>0:\;\forall x\in U_<\delta>(a)\rightarrow|f(x)|\leq C\nonumber
$$

Если функция \(f\) непрерывна в точке \(a\), причем \(f(a)\neq 0\), то в некоторой окрестности точки \(a\) знак функции совпадает со знаком числа \(f(a)\), то есть
$$
\exists\delta>0:\quad\forall x\in U_<\delta>(a)\rightarrow \operatorname\ f(x)=\operatorname\ f(a).\nonumber
$$

\(\circ\) Эти утверждения следуют из свойств пределов. \(\bullet\)

Непрерывность суммы, произведения и частного.

Если функции \(f\) и \(g\) непрерывны в точке \(a\), то функции \(f+g\), \(fg\) и \(f/g\) (при условии \(g(a)\neq 0\)) непрерывны в точке \(a\).

\(\circ\) Это утверждение следует из определения непрерывности и свойств пределов. \(\bullet\)

Непрерывность сложной функции.

Напомним, что такое сложная функция.

Пусть функции \(y=\varphi(x)\) и \(z=f(y)\) определены на множествах \(X\) и \(Y\) соответственно, причем множество значений функции \(\varphi\) содержится в области определения функции \(f\). Тогда функция, которая принимает при каждом \(x\in X\) значение \(F(x)=f(\varphi(x))\), называется сложной функцией или суперпозицией (композицией) функций \(\varphi\) и \(f\).

Если функция \(z=f(y)\) непрерывна в точке \(y_0\), а функция \(y=\varphi(x)\) непрерывна в точке \(x_0\), причем \(y_0=\varphi(x_0)\), то в некоторой окрестности точки \(x_0\) определена сложная функция \(f(\varphi(x_0))\), и эта функция непрерывна в точке \(x_0\).

\(\circ\) Пусть задано произвольное число \(\varepsilon>0\). В силу непрерывности функции \(f\) в точке \(y_0\) существует число \(\rho=\rho(\varepsilon)>0\) такое, что \(U_\rho(y_0)\subset D(f)\) и
$$
\forall y\in U_\rho(y_0)\rightarrow f(y)\in U_<\varepsilon>(z_<0>),\label
$$
где \(z_<0>=f(y_<0>)\).

В силу непрерывности функции \(\varphi\) в точке \(x_<0>\) для найденного в \eqref числа \(\rho>0\) можно указать число \(\delta=\delta_<\rho>=\delta(\varepsilon)>0\) такое, что
$$
\forall x\in U_\delta(x_0)\rightarrow \phi (x)\in U_\rho (y_0).\label
$$

Из условий \eqref и \eqref следует, что на множестве \(U_\delta(x_0)\) определена сложная функция \(f(\varphi(x))\), причем
$$
\forall x\in U_\delta(x_0)\rightarrow f(y)=f(\varphi(x))\in U_<\varepsilon>(z_<0>),\nonumber
$$
где \(z_0=f(\varphi(x_0))=f(y_<0>)\), то есть
$$
\forall \varepsilon>0\;\exists \delta>0:\quad \forall х\in U_\delta(x_0)\rightarrow f(\varphi(х))\in U_\varepsilon(\varphi(x_0)).\nonumber
$$

Это означает, в силу определения непрерывности, что функция \(f(\varphi(x))\) непрерывна в точке \(x_0\). \(\bullet\)

Соответствие между окрестностями точек \(x_0,\ y_0,\ z_0\) представлено на рис. 11.1. По заданному числу \(\varepsilon>0\) сначала находим \(\rho>0\), а затем для чисел \(\rho>0\) находим \(\delta>0\).

Рис. 11.1

Свойства функций, непрерывных на отрезке.

Функцию \(f(x)\) называют непрерывной на отрезке \([a,b]\), если она непрерывна в каждой точке интервала \((a,b)\) и, кроме того, непрерывна справа в точке \(a\) и непрерывна слева в точке \(b\).

Ограниченность непрерывной на отрезке функции.

Если функция \(f\) непрерывна на отрезке \([a,b]\), то она ограничена, то есть
$$
\exists C>0:\forall x\in[a,\ b]\rightarrow|f(x)|\leq C.\label
$$

\(\circ\) Предположим противное, тогда
$$
\forall C>0\;\exists x_\in [a,b]:\;|f(x_)|>C.\label
$$

Полагая в этом выражении \(C=1,2\ldots,n,\ldots,\) получим, что
$$
\forall n\in\mathbb\quad\exists x_\in[a,b]:\;|f(x_)|>n.\label
$$

Последовательность \(x_n\) ограничена, так как \(a\leq x_\leq b\) для всех \(n\in\mathbb\). По теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность, то есть существуют подпоследовательность \(x_\) и точка \(\xi\) такие, что
$$
\lim_x_>=\xi,\label
$$
где в силу условия \eqref для любого \(k\in\mathbb\) выполняется неравенство
$$
a\leq x_>\leq b.\label
$$

Из условий \eqref и \eqref следует, что \(\xi\in [а,b]\) а из условия \eqref в силу непрерывности функции \(f\) в точке \(\xi\) получаем
$$
\displaystyle \lim_f(x_>)=f(\xi).\label
$$

С другой стороны. утверждение \eqref выполняется при всех \(n\in\mathbb\) и, в частности, при \(n=n_k\;(k=1,2,\ldots)\), то есть
$$
|f(x_>)|>n_,\nonumber
$$
откуда следует, что \(\displaystyle \lim_f(x_>)=\infty\), так как \(n_\rightarrow +\infty\) при \(k\rightarrow\infty\). Это противоречит равенству \eqref, согласно которому последовательность \(\>)\>\) имеет конечный предел. По этому условие \eqref не может выполняться, то есть справедливо утверждение \eqref. \(\bullet\)

Теорема Вейерштрасса неверна для промежутков, не являющихся отрезками. Например, функция \(f(x)=\displaystyle \frac<1>\) непрерывна на интервале \((0,1)\), но не ограничена на этом интервале. Функция \(f(x)=x^<2>\) непрерывна на \(\mathbb\), но не ограничена на \(\mathbb\).

Достижимость точных граней.

Если функция \(f\) непрерывна на отрезке \([a,b]\), то она достигает своей точной верхней и нижней грани, то есть
$$
\exists\xi\in[a,b]:\quad f(\xi)=\sup_ f(x),\label
$$

\(\circ\) Так как непрерывная на отрезке функция \(f(x)\) ограничена (теорема 3), то есть множество значений, принимаемых функцией \(f\) на отрезке \([a,b]\), ограничено, то существуют \(\displaystyle \sup_f(x)\) и \(\displaystyle \inf_f(x)\).

Докажем утверждение \eqref. Обозначим \(M=\displaystyle \sup_f(x)\). В силу определения точной верхней грани выполняются условия
$$
\forall х\in [a,b]\rightarrow f(x)\leq M,\label
$$
$$
\forall\varepsilon>0\;\exists x(\varepsilon)\in[a,b]:\quad f(x(\varepsilon))>M-\varepsilon.\label
$$

Полагая \(\varepsilon=\displaystyle \frac<1><2>, \displaystyle \frac<1><3>,\ldots,\frac<1>,\ldots\), получим в силу условия \eqref последовательность\(\\), где \(x_n=\displaystyle x\left(\frac1n\right)\), такую, что для всех \(n\in\mathbb\) выполняются условия
$$
x_n\in [a,b],\label
$$
$$
f(x_)>M-\displaystyle \frac<1>.\label
$$

Из соотношений \eqref, \eqref и \eqref следует, что
$$
\forall n\in\mathbb\rightarrow M-\frac<1>\; Замечание 4

Теорема 4 неверна для интервалов: функция, непрерывная на интервале, может не достигать своих точных граней. Например, функция \(f(x)=x^<2>\) не достигает на интервале (0,1) своей точной нижней грани, равной нулю, и точной верхней грани, равной единице.

Промежуточные значения.

(теорема Коши о нулях непрерывной функции)

Если функция \(f\) непрерывна на отрезке [a,b] и принимает в его концах значения разных знаков, то есть \(f(a)f(b)\; Доказательство

\(\circ\) Разделим отрезок \([a,b]\) пополам. Пусть \(d\) — середина этого отрезка. Если \(f(d)=0\), то теорема доказана, а если \(f(d)\neq 0\), то в концах одного из отрезков \([a,d],\ [d,b]\) функция \(f\) принимает значения разных знаков. Обозначим этот отрезок \(\Delta_<1>=[a_<1>,b_<1>]\). Пусть \(d_<1>\) — середина отрезка \(\Delta_1\). Возможны два случая:

Продолжая эти рассуждения, получим:

С другой стороны, из неравенства \eqref следует, что \(b_-a_\rightarrow 0\) при \(n\rightarrow\infty\), и поэтому
$$
\exists n_0\in\mathbb:\quad b_>-a_>\; Замечание 5

Теорема 5 утверждает, что график функции \(y=f(x)\), непрерывной на отрезке \([a,b]\) и принимающей в его концах значения разных знаков, пересекает ось \(Ox\) (рис. 11.2) хотя бы в одной точке отрезка \([a,b]\).

Рис. 11.2

(теорема Коши о промежуточных значениях)

Если функция \(f\) непрерывна на отрезке \([a,b]\) и \(f(a)\neq (b)\), то для каждого значения \(C\), заключенного между \(f(a)\) и \(f(b)\), найдется точка \(\xi\in [a,b]\) такая, что \(f(\xi)=C\).

\(\circ\) Обозначим \(f(a)=A,\ f(b)=B\). По условию \(А\neq В\). Пусть, например, \(A 0\) и по теореме 5 найдется точка \(\xi\in [a,b]\) такая, что \(\varpi(\xi)=0\), то есть \(f(\xi)=C\). Утверждение \eqref доказано. \(\bullet\)

Если функция \(f\) непрерывна на отрезке \([a,b],\ m=\displaystyle \inf_ f(x),\ M=\displaystyle \sup_ f(x)\), то множество значений, принимаемых функцией \(f\) на отрезке \([a,b]\), есть отрезок \([m,M]\).

\(\circ\) Для всех \(x\in[a,b]\) выполняется неравенство \(m\leq f(x)\leq M\), причем согласно теореме 4 функция \(f\) принимает на отрезке \([a,b]\) значения, равные \(m\) и \(М\). Все значения из отрезка \([m,M]\) функция принимает по теореме 6. Отрезок \([m,M]\) вырождается в точку, если \(f(x)=const\) на отрезке \([a,b]\). \(\bullet\)

Существование и непрерывность функции, обратной для непрерывной и строго монотонной функции.

Ранее мы уже рассматривали понятие обратной функции. Докажем теорему о существовании и непрерывности обратной функции.

Если функция \(y=f(x)\) непрерывна и строго возрастает на отрезке \([a,b]\), то на отрезке \([f(a),(b)]\) определена функция \(x=g(y)\), обратная к f, непрерывная и строго возрастающая.

\(\circ\) Существование обратной функции. Обозначим \(A=f(a),\;B=f(b)\). Так как f — возрастающая функция, то для всех \(х\in [a,b]\) выполняется неравенство \(A\leq f(x)\leq B\), где \(A= \displaystyle \inf_ f(x),\;B=\sup_f(x)\), и в силу непрерывности f (следствие из теоремы 6) множество значений функции \(E(f)=[A,B]\).

Согласно определению обратной функции (\S\ 9,п. 9) нужно доказать, что для каждого \(у_0\in [A,В]\) уравнение
$$
f(x)=y_<0>\label
$$
имеет единственный корень \(x=x_<0>\), причем \(x_0\in [a,b]\).

Существование хотя бы одного корня уравнения \eqref следует из теоремы 6. Докажем, что уравнение \eqref имеет на отрезке \([a,b]\) единственный корень.

Предположим, что наряду с корнем \(x=x_<0>\) уравнение \eqref имеет еще один корень \(x=\widetilde_<0>\), где \(\widetilde_<0>\neq x_0\); тогда \(f(\widetilde)=y_<0>,\;\widetilde x_0\in[a,b]\).

Пусть, например, \(\widetilde_0>x_0\). Тогда в силу строгого возрастания функции \(f\) на отрезке \([a,b]\) выполняется неравенство \(f(\widetilde_0)>f(x_<0>)\). С другой стороны, \(f(\widetilde_0)=f(x_0)=y_<0>\). Отсюда следует, что неравенство \(\widetilde_0>x_<0>\) не может выполняться. Следовательно, \(\widetilde_0=x_0\). Существование обратной функции доказано, то есть на отрезке \([A,В]\) определена функция \(x=f^<-1>(y)=g(y)\), обратная к \(f\), причем \((g)=[a,b]\) и
$$
g(f(x))=x,\quad x\in[a,b],\quad f(g(y))=y,\quad u\in [A,B].\label
$$

Монотонность обратной функции. Докажем, что \(g(y)\) — строго возрастающая на отрезке [A,В] функция, то есть
$$
\forall\;y_<1>,\;y_<2>\in [A,B]:\quad y_<1>\; Замечание 6

Если функция \(f\) непрерывна и строго убывает на отрезке \([a,b]\), то обратная к ней функция \(g\) непрерывна и строго убывает на отрезке \([f(b),f(a)]\).

Аналогично формулируется и доказывается теорема о функции \(g\), обратной к функции \(f\), для случаев, когда функция \(f\) задана на интервале (конечном либо бесконечном) и полуинтервале.
Если функция \(f\) определена, строго возрастает и непрерывна на интервале \((a,b)\), то обратная функция \(g\) определена, строго возрастает и непрерывна на интервале \((A,B)\), где
$$
A=\lim_f(x),\quad B=\lim_f(x).\nonumber
$$

Источник

Непрерывность функций – теоремы и свойства

Определение непрерывности функции

Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x ₀ , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x ₀ равен значению функции в x ₀ :
.

Свойства непрерывных в точке функций

Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.

Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».

Непрерывность сложной функции

Предел сложной функции

Точки разрыва

Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.

Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.

Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.

Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Свойства функций, непрерывных на отрезке

Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.

Обратные функции

Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.

Свойства и непрерывность элементарных функций

Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.

Показательная функция

Логарифм

Экспонента и натуральный логарифм

Степенная функция

Тригонометрические функции

Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.

Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Непрерывность функций с примерами решения и образцами выполнения

Непрерывность функции:

Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.

Определение:

Функция у = f(x) называется непрерывной в точке х₀, если:

Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.

Пример:

Исследовать на непрерывность функцию 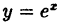в точке х = 1.

Решение:

Чтобы доказать, что функция 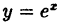непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):

Таким образом, доказано, что функция 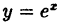непрерывна в точке х = 1.

Замечание:

Формулу (10.1) можно записать в виде
(10.2)
так как 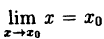. Это значит, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.

Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 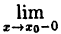f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.

Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:

Определение:

Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)

Пример:

Показать, что функция у = х³ непрерывна для любого значения аргумента х.

Решение:

Найдем приращение функции ∆y.

Используя теоремы о пределе суммы и произведения функции, получим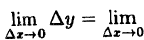
(3x²∆x 4- 3x∆x² + ∆x³) = 0.

Следовательно, функция у = х³ непрерывна при — ∞ Точки разрыва функции и их классификация

Определение:

Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.

Так, например, функция 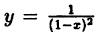(рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.

Рис. 89. График функции

Определение:

Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.

Пример:

Исследовать на непрерывность функцию

Решение:

В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 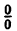. В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить:

Определение:

Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.

Пример:

Исследовать на непрерывность функцию
(рис. 90).

Рис. 90. График функции

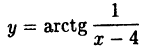
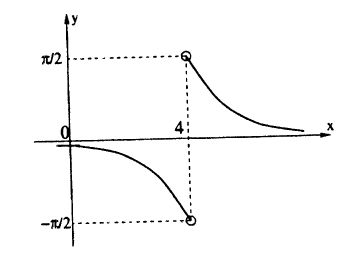
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.

Предел слева —.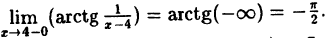
Предел справа — .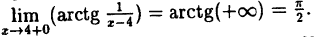
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).

Определение:

Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.

В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 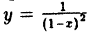, представленная на рис. 89, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.

Действия над непрерывными функциями

Теорема:

Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.

Докажем непрерывность произведения.

Дано: непрерывность функций в точке x₀:
и

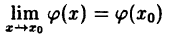
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. f(x) — f(x₀).

Доказательство:
f(x) = [ϕ(x) ∙ ψ(x)] = ϕ(x) ∙ ψ(x) = ϕ(x₀) ∙ ψ(x₀) = f(x₀).

Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.

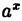
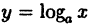
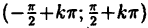
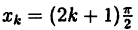
Например, степенная у = xⁿ, показательная у = , тригонометрические у = sin х и у = cos х функции непрерывны на всей числовой оси (х ∈ R), логарифмическая функция непрерывна при х > 0, а тригонометрическая у = tg x непрерывна в каждом из интервалов и терпит разрыв II рода в точках (k = 0; ±1; ±2;…).

Теорема:

Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.

В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.

Пример:

Вычислить

Решение:

Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 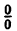. Выполним преобразование

Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( f(x)= f (x)).

но — второй замечательный предел.

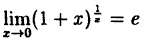
Следовательно,
(10.4)

В частности, при а = е
(10.5)

Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.

Пример:

Вычислить

Решение:

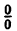
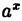
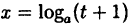
Здесь мы имеем дело с неопределенностью вида . Для нахождения предела сделаем замену переменной, положив — 1 = t. Тогда . При х → 0 также и t → 0.

Так как на основании результата, полученного в предыдущем примере, 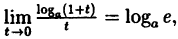то
(10.6)

В частности, если а = е, имеем

т.е. у = 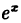— 1 и y = x — эквивалентные бесконечно малые функции при х → 0.

Свойства функций, непрерывных на сегменте

Определение:

Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.

Теорема:

Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.

Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.

Рис. 91. Геометрическая иллюстрация условий теоремы 10.3

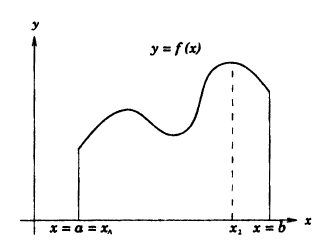
Следствие:

Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.

Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].

Теорема:

Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.

Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.

Рис. 92. Геометрическая иллюстрация условий теоремы 10.4

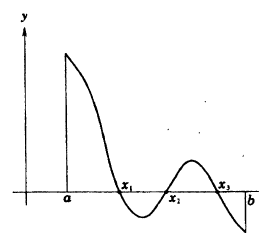
Теорема:

О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.

Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.

Рис. 93. Геометрическая иллюстрация условий теоремы 10.5

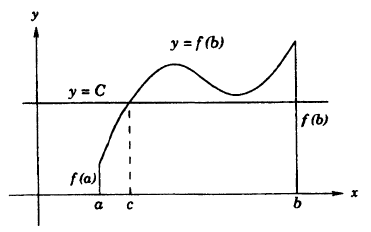
Теорема:

О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.

Эту теорему мы принимаем без доказательства.

Решение на тему: Непрерывная функция

Пример:

Показать, что функция у = 4x² непрерывна в точке х = 2.

Решение:

Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:

1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
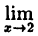
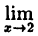
2) существует f(x) = 4x²= 16;
3) этот предел равен значению функции в точке х = 2

f(x) = f(2) = 16.

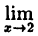
Пример:

Показать, что функция у = sin x непрерывна для любого значения аргумента х.

Решение:

Найдем приращение функции ∆y, используя формулы тригонометрических тождеств

Так как 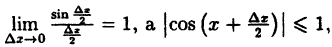то при любом х имеем

Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :

Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).

Пример:

Исследовать на непрерывность функцию

Решение:

В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что

Следовательно, точка х = 5 точка устранимого разрыва.

Пример:

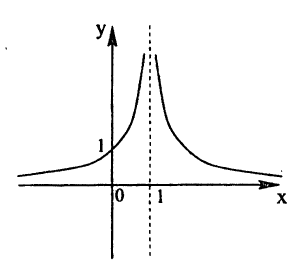
Исследовать на непрерывность функцию

Решение:

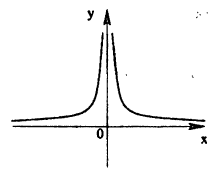
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго

Пример:

Исследовать на непрерывность функцию

Решение:

В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа

Рис. 95. График функции

Пример:

Исследовать на непрерывность функцию .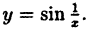

Решение:

Рис. 96. График функции

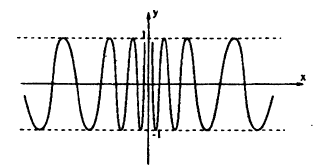
Пример:

Исследовать на непрерывность функцию

Решение:

Функция 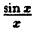не определена в точке х = 0. Точка х = 0 является точкой разрыва I рода, так как при х → 0 существуют пределы справа и слева:

Если доопределить функцию 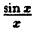в точке х = 0, полагая f(0) = 1, то получим уже непрерывную функцию, определенную так:
f(х) =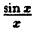, если х ≠ 0; f(0) = 1.

Доопределив функцию в точке х = 0, мы устранили разрыв.

Непрерывность функций

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник