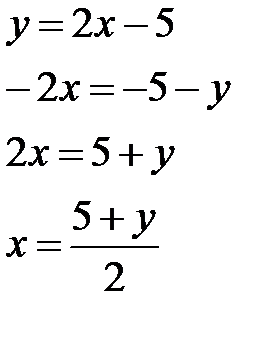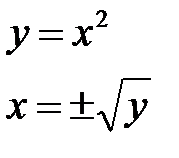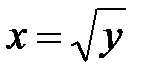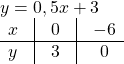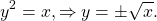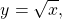Как доказать что функция обратима

Взаимно обратные функции, основные определения, свойства, графики

Понятие обратной функции

Для чего вообще нам нужно понятие обратных функций?

Нахождение взаимно обратных функций

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным.

Решение

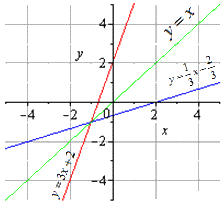
Обе взаимно обратные функции можно отобразить на графике следующим образом:

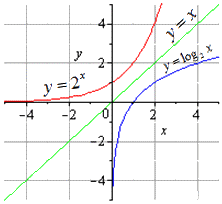
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Решение

В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.

На графике обе функции будут выглядеть так:

Основные свойства взаимно обратных функций

a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3

Графики взаимно обратных функций

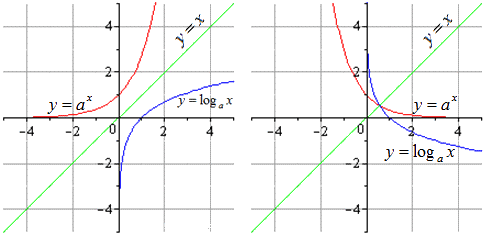
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

Графики для функций с a > 1 и a 1 будут выглядеть так:

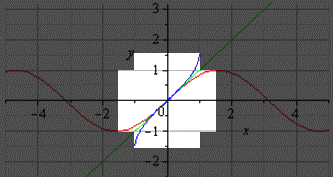
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

График главной ветви косинуса и арккосинуса выглядит так:

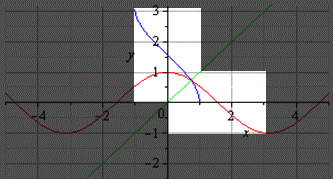
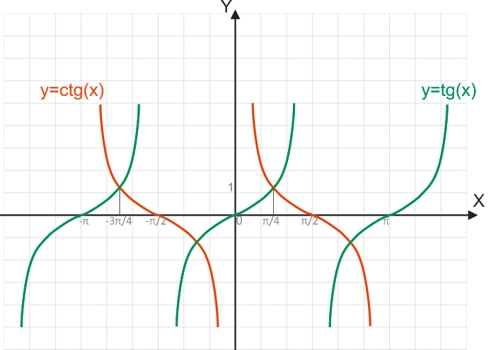
График главной ветви арктангенса и тангенса:

График главной ветви арккотангенса и котангенса будет таким:

Это все свойства обратных функций, о которых мы хотели бы вам рассказать.

Источник

Обратимые и обратные функции

Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.

Примеры обратимых функций:

Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.

Примеры обратных функций:

Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:

Графики функций будут симметричны относительно прямой y=x:

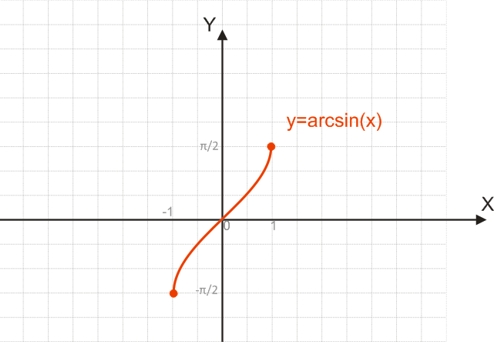
Функция y=arcsin(x)

Поскольку функция y=sin(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=sin(x), необходимо взять один из полупериодов функции, обычно это отрезок [-π/2;π/2], на котором функция обратима.

График функции y=arcsin(x):

Например, чтобы найти arcsin(1), можно воспользоваться равенством 1=sin(y). Угол на отрезке [-π/2;π/2], синус которого равняется 1, будет равен 90° или π/2.

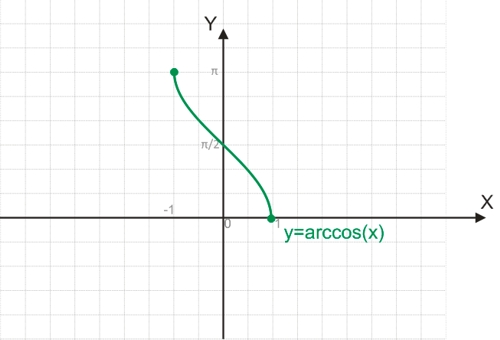
Функция y=arccos(x)

Поскольку функция y=cos(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=cos(x), необходимо взять один из полупериодов функции, обычно это отрезок [0;π], на котором функция обратима.

График функции y=arccos(x):

Например, чтобы найти arccos(1), можно воспользоваться равенством 1=cos(y). Угол на отрезке [0;π], косинус которого равняется 1, будет равен 0.

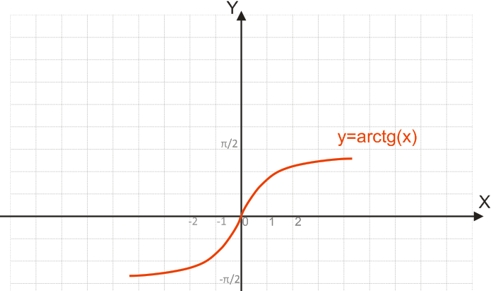
Функция y=arctg(x)

Поскольку функция y=tg(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=tg(x), необходимо рассматривать тангенсоиду на отрезке [-π/2;π/2], на котором функция обратима.

График функции y=arctg(x):

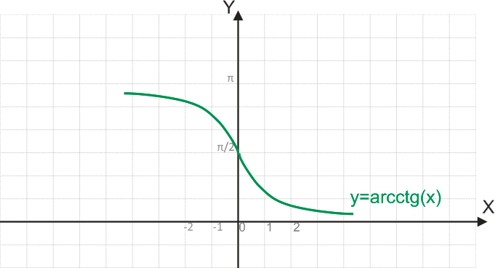
Функция y=arcctg(x)

Поскольку функция y=ctg(x) является периодической, она не является обратимой.

Для построения функции, обратимой y=ctg(x), необходимо рассматривать котангенсоиду на отрезке [0;π], на котором функция обратима.

График функции y=arcctg(x):

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

АЛГОРИТМ СОСТАВЛЕНИЯ ОБРАТНОЙ ФУНКЦИИ.

Лекция по теме «Обратная функция»

ПОНЯТИЕ ОБРАТИМОЙ ФУНКЦИИ.

ДОСТАТОЧНОЕ УСЛОВИЕ ОБРАТИМОСТИ.

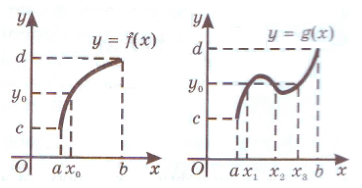
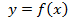
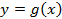
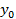
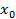
На рисунках приведены две функции, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет (рис.1). Таким образом, функция обладает свойством, не характерным для функции : какое бы число из множества значения функции f(x) ни взять, оно является значением функции только в одной точке . Говорят, что такая функция обратима.

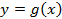
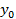
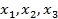
У функции значение можно получить сразу в трех точках . Поэтому такая функция не обратима.

Определение 1. Функцию 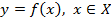называют обратимой, если любое свое значение она принимает только в одной точке множества X.

Теорема. Если функция 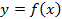монотонна на множестве X, то она обратима.

Попробуйте самостоятельно определить, какая из предложенных функций обратима?:

а)

б)

а) – функция и возрастает и убывает, значит, она немонотонна, поэтому необратима

б) – функция убывает, значит, она монотонна, поэтому обратима

в) – линейная функция, k=2, то есть функция возрастает, значит, она монотонна, поэтому обратима

г) – квадратичная функция, график – парабола, ветви вниз, то есть функция и возрастает и убывает, значит, она немонотонна, поэтому необратима

Замечание. Монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.

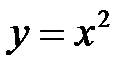
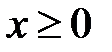
Например, мы можем взять немонотонную функцию и рассмотреть ее только на одном промежутке, где она только возрастает или только убывает, тогда условие обратимости будет выполняться. Например, функция при будет возрастающей функцией, поэтому при таких значениях х она обратима.

ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ.

АЛГОРИТМ СОСТАВЛЕНИЯ ОБРАТНОЙ ФУНКЦИИ.

Алгоритм составления обратной функции для функции y=f(x), .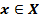

Пример 1. Показать, что для функции y=2x-5 существует обратная функция, и найти ее аналитическое выражение.

Решение. Линейная функция y=2x-5 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение 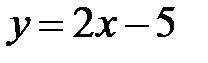относительно х;

Переобозначим переменные, получим искомую обратную функцию

Она определена и возрастает на R.

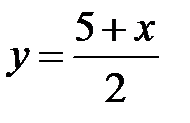
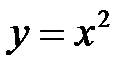
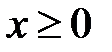
Пример 2. Показать, что для функции при существует обратная функция, и найти ее аналитическое выражение.

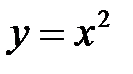
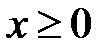
Решение. – квадратичная функция. При функция непрерывна, монотонно возрастает в своей области определения, следовательно, она обратима. Найдем ее:

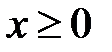
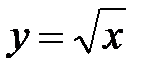
Так как по условию , то

– обратная функция для

Источник

Обратная функция

Что такое обратная функция? Как найти функцию, обратную данной?

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо :

1) В формулу функции вместо y подставить x, вместо x — y:

2) Из полученного равенства выразить y через x:

Найти функцию, обратную функции y=2x-6.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).

Теорема (необходимое и достаточное условие обратимости функции)

Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.

Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.

Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.

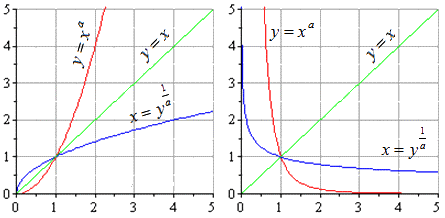
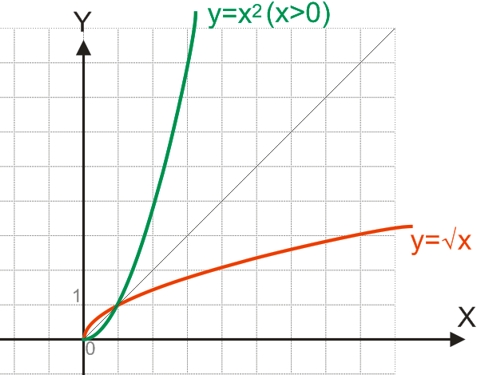
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.

Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).

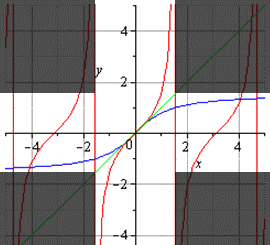
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:

В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.

1 комментарий

Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?

Источник

Взаимно обратные функции

Функция, обратная данной

По определению (см. §34 справочника для 7 класса)

Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Пусть некоторое соответствие задано таблицей:

Алгоритм вывода формулы функции, обратной данной

Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.

Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.

Шаг 3. Ограничений на x и y нет

Шаг 3. Ограничений на x и y нет

Шаг 3. На исходную функцию накладываются ограничения

Шаг 3. На обратную функцию накладываются ограничения

Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.

Свойства взаимно обратных функций

1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.

2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.

4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.

5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.

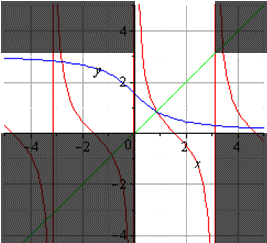
Графики пар взаимно обратных функций, найденных выше:

Примеры

Пример 1. Задайте формулой функцию, обратную данной.

Меняем аргумент и значение: x = 5y-4

Меняем аргумент и значение: x = 4y+1

$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$

Пример 2. Найдите функцию, обратную данной.

Постройте график исходной и обратной функции в одной системе координат.

$x = y^2 \Rightarrow y = \pm \sqrt$

$x = y-3 \Rightarrow y = x+3$

$x = \frac<1> \Rightarrow y = \frac<1> -1$

$x = 1+ \sqrt \Rightarrow y = (x-1)^2+3$

Источник