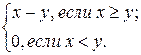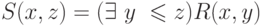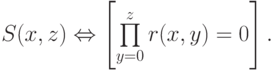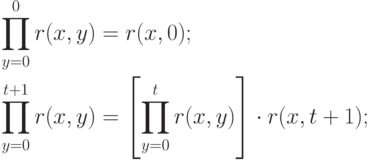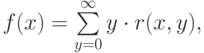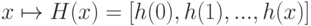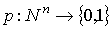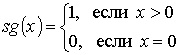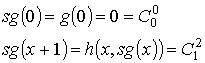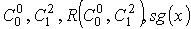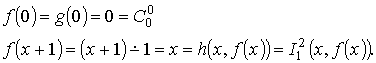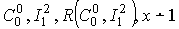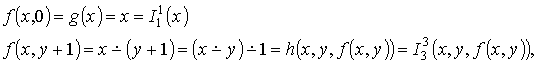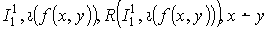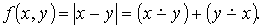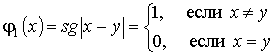Как доказать что функция примитивно рекурсивная

Примитивно рекурсивные функции

Содержание

Рекурсивные функции [ править ]

Строительные блоки рекурсивных функций [ править ]

Рассмотрим примитивы, из которых будем собирать выражения:

Примитивно рекурсивные функции [ править ]

Благодаря проекторам мы можем делать следующие преобразования:

Арифметические операции на примитивно рекурсивных функциях [ править ]

n-местный ноль [ править ]

[math] \textbf 0 [/math] — функция нуля аргументов.

[math] \textbf 0^<1>(y) = \mathrm(y) [/math]

[math] \textbf 0^(x_1,\ldots,x_,y) = \mathrm(y) [/math]

Константа [math] \textbf M [/math] [ править ]

Сложение [ править ]

[math] \mathrm(x) = x [/math]

[math] \mathrm(x, y, z) = \mathrm(z) [/math]

[math] \mathrm\langle<>\mathrm,\mathrm\rangle (x,y) = \left\<\begin \mathrm(x) & y = 0\\ \mathrm(x, y-1,\mathrm\langle<>\mathrm,\mathrm\rangle(x, y-1)) & y \gt 0 \end\right.[/math]

[math]=\left\ <\begin x & y = 0\\ \mathrm(\mathrm \langle<>\mathrm,\mathrm\rangle(x, y-1)) & y \gt 0 \end\right.[/math]

[math]=\left\ <\begin x & y = 0\\ \mathrm(\mathrm(x, y-1)) & y \gt 0 \end\right. [/math]

Можно преобразовать в более простой вид.

[math] \mathrm(x,0) = x [/math]

[math] \mathrm(x,y) = \mathrm (\mathrm(x,y-1)) [/math]

Умножения [ править ]

[math] \mathrm(x,0) = \mathrm(x) [/math]

Вычитания [ править ]

[math] \mathrm(0) = \mathrm(0) [/math]

[math] \mathrm(x+1) = x [/math]

Теперь рассмотрим [math] \mathrm_{(x,y) [/math]}

[math] \mathrm_{(x,0) = x [/math]}

Операции сравнения [ править ]

Сначала выразим [math] \mathrm>(x) = \mathrm(x,0) [/math]

[math] \mathrm(0) =\mathrm(0) [/math]

Теперь все остальные функции

[math] \mathrm(x,y) = \mathrm(\mathrm(x,y),\mathrm(y,x)) [/math]

Условный оператор [ править ]

[math] \mathrm(0,x,y) = y [/math]

[math] \mathrm(c,x,y) = x [/math]

Деление [ править ]

Теперь само деления

[math] \mathrm(0,y) = \mathrm(y) [/math]

Остаток от деления выражается так:

Работа со списками фиксированной длины [ править ]

Теоремы [ править ]

Теорема о примитивной рекурсивности вычислимых функций [ править ]

[math] \mathrm([L,R,S,C],t) = [L,R,S,C] [/math]

Источник

Операция примитивной рекурсии

Будем говорить, что (n+1) – местная функция f получается из n – местной функции g и (n+2) – местной функции h с помощью операции примитивной рекурсии, если при любых значениях x₁, x₂,…, x_n выполняются равенства:

Эти равенства называют схемой примитивной рекурсии. И тот факт, что функция f получается из функций g, h c помощью операции примитивной рекурсии, записывается следующим образом: f=R(g,h).

Определение 1 Функция f называется примитивно рекурсивной функцией, если она получается из простейших функций с помощью операций суперпозиции и примитивной рекурсии, взятых конечное число раз в любой последовательности.

Из данного определения следует, что любая примитивно рекурсивная функция является числовой функцией.

Множество всех примитивно рекурсивных функций обозначим через P_n.p.

Пример 5 Доказать, что функция f(x,y)= x+y примитивно рекурсивна.

Действительно. Справедливы следующие тождества

Отсюда следует, что x+y = R(g(x) = x, h(x,y,z) = z+1). Так как функции g, h – простейшие функции, то x + y 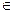P_n.p.

Пример 6 Доказать, что функция f(x,y) = x?y примитивно рекурсивна.

Действительно. Справедливы следующие тождества:

f(x,y+1) = x(y+1) = xy+x = f(x, y) + x

Отсюда следует, что

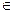
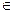
Как следует из примера 1 функция h(x,y,z) = x+z P_n.p. А это значит, что xy P_n.p.

Рассмотрим функцию x 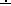y =

Пример 7 Показать, что функция f(x,y) = x 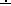y примитивно рекурсивна.

В начале заметим, что функция x 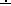1 примитивно рекурсивна. Действительно:

0 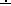1 = 0 = g(x)

(x+1) 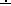1 = x = h(x,y)

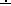
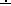
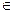
Следовательно, x 1 = R(g(x) = 0, h(x,y) = x). Итак, x 1 P_n.p.

Далее, нетрудно показать, исходя из определения усечённой разности, что эти функции удовлетворяют также равенствам:

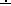
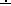
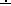
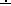
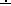
x 0 = x = g(x)

x (y+1) = (x y) 1 = h(x, y, x y)

для любых x и y. Данные тождества показывают, что

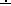
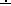
x y = R(g(x) = 0, h(x,y,z) = z α).

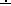
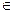
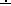
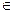
Так как функция h(x,y,z) = z α P_n.p., то x y P_n.p.

Так как любая примитивно рекурсивная функция является числовой функцией, то, очевидно, что x – y 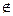P_n.p.

Пример 8 Покажем, что 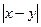– примитивно рекурсивная функция.

Действительно. Нетрудно показать, что 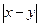=(x y)+(y x). Теперь полученный результат следует из примера 5 и примера 7.

Операция минимизации. Будем говорить, что n-местная функция g(x₁,x₂,…,x_n) полученная из (n+1)-местной функции f(x₁,x₂,…,x_n,y) с помощью операции минимизации или оператора наименьшего числа, если для любых x₁, x₂,…, x_n, y равенство g(x₁,x₂,…,x_n) = y выполняется тогда и только тогда, когда:

Используется следующее обозначение:

Про функцию g говорят, что она получена из функции f при помощи операции минимизации.

Определение 2 Функция f называется частично рекурсивной функцией, если она может быть получена из простейших функций с помощью операции суперпозиции, примитивной рекурсии и минимизации, взятых конечное число раз в любой последовательности.

Класс частично рекурсивных функций обозначим P_rp.

Обозначим через P_p ­­– класс рекурсивных функций, т.е. всех числовых функций из P_rp.

Пример 9 Доказать, что частично числовая функция 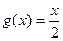частично рекурсивна.

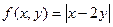
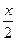
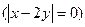
Вначале заметим, что данная функция получается из функции с помощью операции минимизации, т.е. = M_y .

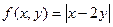
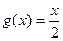
Согласно примерам 2 и 4 функция примитивно рекурсивна. А это значит, что – частично рекурсивная функция.

Данный пример показывает, что класс P_rp существенно шире, чем класс P_p. Можно сказать, что и класс P_p существенно шире, чем класс P_np, т.е.

Источник

Рекурсивные функции

Примитивно рекурсивные множества

Будем называть множество примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна. (Вариант: если оно является множеством нулей примитивно рекурсивной функции ; это то же самое, так как можно сделать подстановку в функцию .)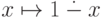

Пересечение и объединение примитивно рекурсивных множеств примитивно рекурсивны (сложим или перемножим функции, множествами нулей которых они являются). Дополнение примитивно рекурсивного множества примитивно рекурсивно. Отождествляя множества со свойствами, можно сказать, что конъюнкции, дизъюнкции и отрицания примитивно рекурсивных свойств будут примитивно рекурсивны.

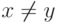
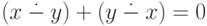
Свойства x=y и примитивно рекурсивны ( x=y тогда и только тогда, когда ).

Теперь можно записать формулу для прибавления единицы по модулю n (для чисел, меньших n ):

После этого функцию x mod n ( остаток от деления на n ) можно определить рекурсивно:

Покажем, что ограниченные кванторы, примененные к примитивно рекурсивным свойствам (множествам ), дают снова примитивно рекурсивные свойства. Это означает, например, что если свойство R(x,y) примитивно рекурсивно, то свойства

А произведение легко определить рекурсивно:

с суммированием можно поступить аналогичным образом.

а суммирование можно ограничить сверху выражением g(x) и воспользоваться примитивной рекурсивностью ограниченной суммы.

Другие виды рекурсии

Мы приведем два примера последнего типа: совместное определение нескольких функций и использование произвольных меньших значений аргумента.

Совместная рекурсия. Пусть две одноместные функции f и g заданы соотношениями:

где a и b некоторые числа, а функции F и G примитивно рекурсивные функции трех аргументов. Покажем, что тогда функции f и g примитивно рекурсивны.

Чтобы доказать это, нам потребуется примитивно рекурсивная нумерация пар такая функция 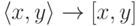(номер пары мы обозначаем квадратными скобками), которая была бы примитивно рекурсивна вместе с двумя обратными функциями (дающими по номеру пары ее первый и второй члены). Тогда мы сможем написать рекурсивное определение для функции h(n)=[f(n),g(n)] :

где функции p₁ и p₂ дают по номеру пары первый и второй ее члены. Если функция h примитивно рекурсивна, то и функции f и g (композиции h с функциями p₁ и p₂ ) также примитивно рекурсивны.

Заметим в заключение, что аналогичная конструкция применима для большего числа одновременно определяемых функций и для функций от большего числа аргументов.

Все эти функции (и другие аналогичные) сводятся к различным операциям с простыми числами и множителями, которые мы в сущности уже разбирали.

Теперь мы докажем, что функция

Источник

Как доказать что функция примитивно рекурсивная

Как нам известно, предикатом называют логическую функцию определенную на заданном множестве объектов. Будем рассматривать в качестве области определения предиката конечный набор, состоящий из натуральных чисел. Таким образом, рассматриваемые предикаты представляют логические функции вида:

В качестве примера предикатов можно привести следующие логические функции:

;
;
.

(17)

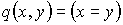
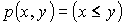
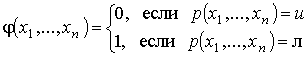
По определению операции примитивной рекурсии получаем, что:

Следовательно, ПРО данной функции является последовательность функций:

Функция f(x,y) = |x-y| определяется следующим образом:

(19)

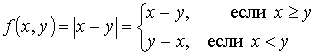
Прежде чем доказать, что функция f(x,y) = |x-y| является примитивно рекурсивной, рассмотрим следующие функции:

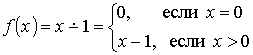
1) (20)
2) (21)

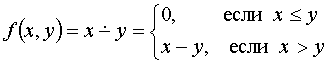
1) Рассмотрим функцию (20). По определения операции примитивной рекурсии получаем, что

Следовательно, ПРО для данной функции является последовательность функций:

2) Рассмотрим теперь функцию (21). По определения операции примитивной рекурсии получаем, что:

Исходя из последнего примера, функцию (19), будем представлять следующим образом:

Теперь можно говорить, что выбранная представляющая функция (18), т.е. φ 1 (x) = sg|x-y| для предиката p 1 (x,y) = (x=y) является ПРФ и удовлетворяет исходным условиям, т.е.

Для предиката p 2 (x,y) = (x в качестве представляющей функции можно брать

Тогда нетрудно проверить, что следующие функции являются представляющими функциями для соответствующих логических операций относительно предикатов, представленных в таблице 1:

(23)
(24)
(25)
(26)

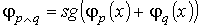
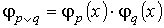
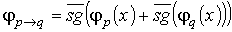
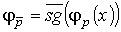
В качестве упражнения, проверьте самостоятельно, что представленные функции действительно удовлетворяют требуемому условию как представляющие функции предиката.

Источник

Примитивно-рекурсивные функции

Пусть заданы функции:

Соотношения (1) и (2) называются схемой примитивной рекурсии. Соотношение (1) задает граничное условие, а соотношение (2) рекурсивно выражает значения функции f через другое значение этой функции.

Предположим, что функции g и h являются вычислимыми. В этом случае функция f также является вычислимой.

2. Используя соотношение (2) и алгоритм вычисления функции h, можно последовательно вычислить значения

ОПРЕДЕЛЕНИЕ

Функции, получаемые из простейших функций с помощью конечного числа применений операций суперпозиции и примитивной рекурсии, называются примитивно-рекурсивными.

Из приведенного определения следует, что всякая примитивно-рекурсивная функция является всюду определенной функцией. Кроме того, все примитивно-рекурсивные функции вычислимы.

Упражнение. Показать, что если f(x₁, x₂) является примитивно-рекурсивной функцией, если она выражается через примитивно-рекурсивные функции g и h с помощью соотношений

f(0, x) = g(x); (1)

f(y+1, x) = h(x, y, f(y, x)). (2)

Доказательство справедливости приведенного в упражнении утверждения обосновывать примитивную рекурсивность функций, определяемых рекурсивными схемами, в которых рекурсия ведется по произвольной переменной.

Рассмотрим примеры примитивно-рекурсивных функций.

1. Сумма f(x, у) = x + у задается следующей схемой примитивной рекурсии:

f(x, 0) = (x);

f(x, у+1) = S(f(x, у)).

2. Произведение p(x, у) = x ´ у задается схемами:

p(x, 0) = O(x);

p(x, у+1) = x+ p(x, у).

Здесь p выражается через функции O(x) и f( 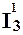(x₁, x₂, x₃), ( x₁, x₂, x₃)), где f — это примитивно-рекурсивная функция из предыдущего примера.

3. Экспонента e(x) = 2 x может быть задана соотношениями:

e(0) = S(0);

e(x+1) = 2×e(x).

Функции S(0(y)) и 2y — примитивно-рекурсивные. Поэтому функция e(x) также является примитивно-рекурсивной.

4. Функции sg(x) и (x), определяемые как:

sg(x) = и (x) = , задаются следующими схемами:

sg(0) = 0; (x) = 1;

sg(x+1) = 1. (x+1) = 0.

d(0) = 0;

d(x+1) = x.

m (x, 0) = x;

m (x, у+1) = d(m(x, у)).

Функции из примеров 5 и 6 являются аналогами арифметического вычитания для множества целых неотрицательных чисел. Такие функции по определению равны нулю, если вычитаемое больше уменьшаемого.

Используя приведенные ранее функции, можно доказывать примитивную рекурсивность и других известных числовых функций.

Например, рассмотрим функцию mod(x,y), принимающую значение, равное остатку от деления числа x на число y.

Для определенности положим, что при делении на нуль остаток всегда равен 0.

Определим mod(x, y) схемой:

mod(0, y) = 0; (1)

Здесь рекурсия ведется по первой переменной.

В соотношении (2) реализовано очевидное свойство остатка от деления значения x+1 на y, которое можно выразить следующим соотношением:

mod(x+1, y) либо равен mod(x, y)+1, если mod(x, y)

Аналогичными соотношениями можно выразить функцию для целочисленного деления div(x, y).

Для определенности будем считать, что div(x, 0) = x, поскольку функция целочисленного деления не является всюду определенной.

div(0, y) = 0;

div(x+1, y) = div(x, y)+ (y-(mod(x, y)+1)).

Например, для функцииmod(x, y) необходимо образовать вспомогательную функциюg(x, y)= mod( (x, y), (x, y)). Такая функция может быть выражена с помощью схемы примитивной рекурсии.

Поэтому mod также является примитивно-рекурсивной функцией, поскольку получается из примитивно-рекурсивной функции g обратной перестановкой переменных.

При обосновании примитивной рекурсивности некоторых функций могут оказаться полезными свойства, доказываемые в следующих теоремах.

ТЕОРЕМА 8.1

Доказательство

Очевидно, что функция f может быть задана следующей схемой примитивной рекурсии:

Источник