Как доказать что функция строго монотонна

Как доказать что функция строго монотонна

Пусть \(y = f\left( x \right)\) является дифференцируемой функцией на интервале \(\left( \right).\) Функция называется возрастающей (или неубывающей ) на данном интервале, если для любых точек \(, \in \left( \right),\) таких, что \( строго возрастающей на интервале \(\left( \right).\)

Аналогично определяются убывающая (или невозрастающая ) и строго убывающая функции.

Если функция \(f\left( x \right)\) дифференцируема на интервале \(\left( \right)\) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Снова рассмотрим функцию \(y = f\left( x \right),\) считая ее дифференцируемой на некотором интервале \(\left( \right).\) Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Поскольку \(f’\left( c \right) \ge 0,\) то правая часть равенства неотрицательна. Следовательно, \[f\left( <> \right) \ge f\left( <> \right).\] т.е. функция \(y = f\left( x \right)\) является возрастающей на интервале \(\left( \right).\)

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая строго возрастающей функции.

\(f’\left( x \right) \ge 0\;\forall\;x \in \left( \right);\)

Производная \(f’\left( x \right)\) тождественно не равна нулю ни в каком промежутке \(\left[ <,> \right] \in \left( \right).\)

Условие \(1\) содержится в теореме \(1\) и является признаком неубывающей функции. Дополнительное условие \(2\) требуется для того, чтобы исключить участки постоянства функции, в которых производная функции \(f\left( x \right)\) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы \(2\) следует такая формулировка достаточного признака:

Соответственно, условие \(f’\left( x \right) строго убывающую функцию.

Число точек, в которых \(f’\left( x \right) = 0,\) является, как правило, конечным. Согласно теореме \(2\), они не могут плотно заполнять какой-либо промежуток в интервале \(\left( \right).\)

Приведем также признак строгого возрастания (убывания) функции в точке:

Если \(f’\left( <> \right) > 0\), то функция \(f\left( x \right)\) строго возрастает в точке \(\);

Если \(f’\left( <> \right) сумма функций \(f + g\) также возрастает (убывает) на этом интервале.

Если функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) то противоположная функция \(-f\) убывает (возрастает) на этом интервале.

Если функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) то обратная функция \(\large\frac<1>\normalsize\) убывает (возрастает) на этом интервале.

Если функции \(f\) и \(g\) возрастают (убывают) на интервале \(\left( \right)\) и, кроме того, \(f \ge 0\), \(g \ge 0\), то произведение функций \(fg\) также возрастает (убывает) на этом интервале.

Если функция \(g\) возрастает (убывает) на интервале \(\left( \right),\) а функция \(f\) возрастает (убывает) на интервале \(\left( \right),\) где \(g:\left( \right) \to \left( \right),\) то композиция функций \(f \circ g\) (т.е. сложная функция \(y = f\left( \right)\) также возрастает (убывает) на интервале \(\left( \right).\)

Данная функция является суммой функций \(\) и \(3.\)

Первую функцию \(\) можно рассматривать как произведение двух одинаковых функций \(\). Из примера \(1\) следует, что квадратичная функция \(\) строго возрастает при \(x \ge 0.\) Следовательно, функция \(\) также строго возрастает при \(x \ge 0\) на основании свойства \(4\).

Второе слагаемое \(3\) представляет собой трехкратную сумму функций \(\) и, поэтому, также является строго возрастающей (на основании свойства \(1\)).

Итак, исходная функция \(f\left( x \right) = + 3\) является суммой двух строго возрастающих функций и, следовательно, также строго возрастает при \(x \ge 0.\)

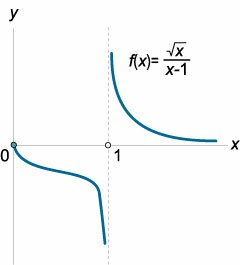
Для контроля рассмотрим также неравенство \(f’\left( x \right) Рис.5

Следовательно, на основании достаточного признака монотонности, функция строго возрастает при \(x \in \left( <\large\frac<1>\normalsize,\infty > \right)\) и строго убывает при \(x \in \left( <0, \large\frac<1>\normalsize> \right).\) Ее вид схематически приведен на рисунке \(10\).

На основании достаточного признака монотонности заключаем, что функция возрастает при \(x \in \left( <0,\large\frac<1><2>\normalsize> \right)\) и убывает при \(x \in \left( <\large\frac<1><2>\normalsize,1> \right).\) График функции представляет собой полуокружность с центром в точке \(\left( <\large\frac<1><2>\normalsize,0> \right)\) и радиусом \(<\large\frac<1><2>\normalsize>\) (рисунок \(14\)).

Источник

Общие сведения

Функцией вида р = f(r) называется зависимость ее значения от переменной величины «r» или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.

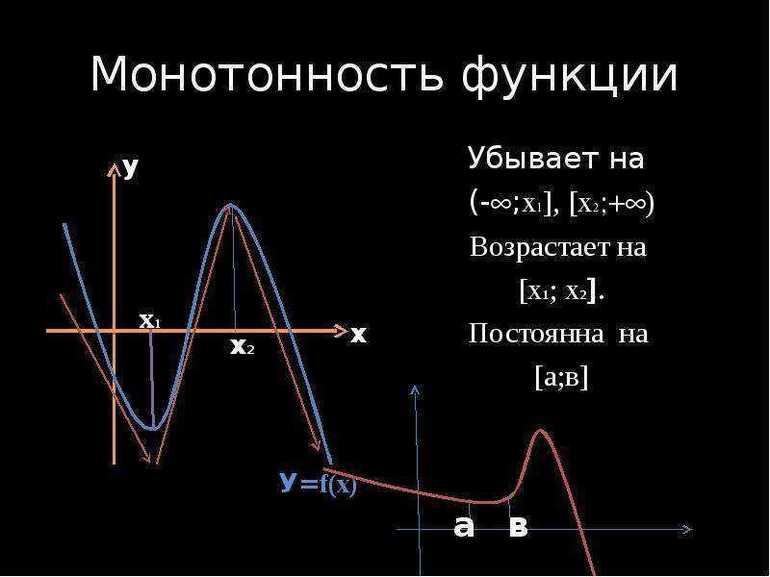
Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) = f(r2) соответственно. Кроме того, нужно учитывать, что r1 =» следует заменить на строгий « »: f(r1) f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:

Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.

Теорема о пределе

Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.

Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.

Критерии возрастания и убывания

Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:

Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) = 0 соответственно (при r ∈ данному интервалу).

Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) 0.

Основные свойства

Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:

После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.

Базовые знания

Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:

Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.

Нахождение производной

Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.

Рисунок 1. Дифференциалы простых выражений.

Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:

Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.

Корни уравнений и критические точки

Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.

Источник

Алгебра

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Возрастание и убывание функций

Посмотрим на график произвольной функции:

Видно, что область определения ф-ции – это промежуток [– 6; 4].

На графике сначала ф-ция как бы «поднимается». При увеличении х растет значение у. Так происходит до точки (1; 5). После этого ситуация меняется, при увеличении аргумента значение ф-ции начинает падать. В математике принято говорить, что ф-ция возрастает на промежутке [– 6; 1] и функция убывает на промежутке [1; 4]. Можно сказать и иначе – ф-ция у является возрастающей функцией на множестве [– 6; 1] и убывающей функцией на множестве [1; 4].

Рассмотрим это определение возрастающей функции подробнее. Построим произвольную возрастающую ф-цию и выберем на ней две точки со значениями аргумента х₁ и х₂. Также отметим значения ф-ции в этих точках, у(х₁) и у(х₂):

По определению, если х₁ меньше х₂, то и у(х₁) »и « у(х₁). По определению получаем, что у = 2х – 3 – возрастающая ф-ция.

Промежутки монотонности основных функций

Мы ранее уже изучили несколько видов ф-ций. Посмотрим, какие у них промежутки монотонности.

Поведение линейной ф-ции у = kх + b зависит исключительно от значение коэффициента k. Если он больше нуля, то функция возрастает на промежутке (– ∞; + ∞), то есть на всей числовой прямой. Если же k n зависит от показателя n. Если он нечетный, то получается ф-ция, возрастающая на всей числовой прямой:

Если же число n четное, то степенная ф-ция будет убывать на промежутке (– ∞:0] и возрастать на промежутке [0; + ∞):

Пример. Найдите значения параметра a, при котором ф-ция

у = (5а – 2)х +16

является возрастающей.

Решение. Данная ф-ция является линейной ф-цией вида у = kx + b, где в роли коэффициента k выступает выражение (5а – 2). Ф-ция будет возрастать, если этот коэффициент будет больше нуля, то есть

Получаем, что ф-ция будет возрастающей при значениях а, больших 0,4, или, другими словами, при а∊(4; + ∞).

Свойства монотонных функций

Монотонные функции имеют ряд примечательных свойств, которые могут помогать при решении задач. Вспомним, что некоторые ф-ции могут при различных значениях аргументов принимать одинаковое значение. Например, таковой является степенная ф-ция у = х 2 :

С точки зрения графиков это означает, что горизонтальная линия может пересекать график ф-ции в нескольких точках:

С другой стороны, это значит, что уравнение х 2 = 4 имеет два корня, 2 и ( – 2).

Если же ф-ция строго монотонна, то такая ситуация невозможна. Любое ее значение может быть получено только при одном значении аргумента.

Действительно, если ф-ция монотонна, то любая горизонтальная прямая сможет пересечь ее график не более чем в одной точке:

Это также означает, что, если у(х) – строго монотонная ф-ция, а b– произвольное число, то уравнение у(х) = b имеет не более одного корня. Так, у уравнения х 3 = 8 есть только один корень (он равен 2), потому что х 3 – монотонная ф-ция.

Рассмотрим следующее свойство монотонных функций.

Действительно, ранее мы уже изучали сжатие и растягивание графиков. умножение ф-ции на постоянное число как раз и ведет к подобным преобразованиям. Ясно, что при этом не происходит изменение монотонности ф-ций:

Например, парабола у = х 2 возрастает на промежутке [0; + ∞), значит, и ф-ция у = 3х 2 также возрастает на этом же промежутке:

Проще говоря, при умножении ф-ции на положительное число ее промежутки монотонности не изменяются.

А что же произойдет при умножении ф-ции на отрицательное число. Она не только сожмется или растянется, но ещё и отобразится симметрично относительно оси Ох. В результате промежутки возрастания ф-ции превратятся в промежутки убывания, и наоборот.

Проиллюстрируем это на примере ф-ций у = х 2 и у = – х 2 :

Видно, что на промежутке (– ∞; 0] ф-ция у = – х 2 возрастает, в то время как обычная парабола убывает. На промежутке [0; + ∞)ситуация противоположная.

Если две ф-ции одновременно возрастают на одном промежутке, то и их сумма также будет возрастать на этом промежутке.

Например, ф-ции у = х 5 и у = 4х возрастают на всей числовой прямой. Следовательно, возрастающей является и ф-ция у = х 5 + 4х.

Пример. Решите уравнение

х 7 + 2х – 3 = 0

Решение. Можно заметить, что число 1 является корнем этого уравнения. Действительно, подставим единицу в уравнение и получим верное равенство:

Докажем, что других корней уравнение не имеет. В его левой части стоит сумма двух возрастающих ф-ций, у = х 7 и у = 2х – 3. Следовательно, и ф-ция у = х 7 + 2х – 3 также является возрастающей на всей числовой прямой. Это значит, что исследуемое уравнение имеет не более 1 корня, то есть корень х = 1 – единственный.

Пример. Докажите, что у уравнения

не более одного корня.

Выражение в левой части имеет смысл только при положительных х. Ведь если х 2 :

В общем случае эту особенность можно доказать так:

у(– х) = (– х) 2 = х 2 = у(х)

В математике есть специальный термин для обозначения ф-ций, обладающих таким свойством. Их называют четным функциями.

Определение четной функции можно записать и так, чтобы в нем фигурировали формулы:

Для проверки того, является ли функция четной, достаточно подставить в нее вместо аргумента х величину (– х).

Пример. Докажите, что ф-ция у = х 4 + 3х 2 является четной.

Решение. Подставим в ф-цию значение (– х):

у(– х) = (– х) 4 + 3(– х) 2 = х 4 + 3х 2

Получили исходную ф-цию у(х). Значит, исследуемая функция является четной.

Пример. Четна ли ф-ция

Решение снова подставим в ф-цию значение (– х):

Получили изначальную ф-цию. Следовательно, она – четная.

Почему же четные ф-ции симметричны относительно оси Оу? Из определения следует, что если графику четной ф-ции принадлежит точка (х₀;у₀), то ему же принадлежит точка (– х₀;у₀). Посмотрим, как они располагаются на координатной плоскости:

Они симметричны относительно оси Оу. Если же для каждой точки графика есть симметричная точка, также ему принадлежащая, то и в целом график симметричен относительно вертикальной оси.

Такая симметрия (относительно точки), называется центральной. Геометрически она означает, каждой точке графика в I четверти с двумя положительными координатами соответствует точка графика в III четверти с такими же координатами, но взятыми со знаком «минус»:

Существует множество ф-ций, обладающих подобной симметрией. В математике их все называют нечетными функциями. У них противоположным значениям аргументов соответствуют противоположные значения ф-ции, а график нечетной функции всегда симметричен относительно начала координат.

Чаще используется определение, содержащее формулу:

Покажем это свойство у ф-ции у = х 3 :

Для того, чтобы доказать нечетность ф-ции, надо поставить в нее (– х) вместо х. Если получилась исходная ф-ция с противоположным знаком, то это значит, что ф-ция нечетная.

Пример. Докажите, что ф-ция у = х 5 + х – нечетная.

Решение: Подставим (– х):

у(– х) = (– х) 5 + (– х) = –х 5 – х = – (х 5 + х) = – у(х)

Получили исходную ф-цию, но со знаком «минус», поэтому ф-ция является нечетной.

Пример. Докажите нечетность ф-ции у = 5/х + 4х.

Решение. Подставляем в ф-цию (– х):

у = 5/(– х) + 4(– х) = – 5/х – 4х = – (5/х + 4х) = – у(х)

Снова получили исходную ф-цию со знаком минус, следовательно, мы исследовали нечетную ф-цию.

Известно, что любое целое число либо четное, либо нечетное. Однако с ф-циями всё по-другому. Существует множество ф-ций, которые не относятся ни к тем, ни к другим. Чтобы доказать, что ф-ция не является ни четной, ни нечетной, достаточно продемонстрировать, что хотя бы для одного значения х не выполняются условия у(– х) = у(х) и у(– х) = – у(х).

Пример. Докажите, что у = х 3 + х 2 – ни четная, ни нечетная ф-ция.

Решение. Определим значение ф-ции при, например, х = 1 и х = –1

у(– 1) = (– 1) 3 + (– 1) 2 = 0

Получили, что при противоположных х значения у не являются ни одинаковыми, ни противоположными. Значит, рассматриваемая ф-ция не подходит под приведенные определения четности и нечетности.

Свойства четных и нечетных функций

Рассмотрим важные свойства, помогающие быстро определять четность и нечетность ф-ций.

Так, ф-ции у = х 3 и у = 1/х – нечетны. Значит, нечетна и их сумма у = х 3 + 1/х.

Другими словами, ф-цию можно «перевернуть», и она всё равно сохранит свою четность. Так, ф-ция 5х 4 + х 2 четная, поэтому и ф-ция

останется такой же.

Вообще рассматриваемое свойство ф-ции часто называют ее четностью. Так, про две рассматриваемые ф-ции у = х 3 и у = х 9 можно сказать, что они обладают одинаковой четностью (обе нечетные), а у = х 5 и у = х 7 обладают различной четностью (одна из них четная, а другая нечетная).

Например, ф-ции у = 5х 3 + 6х и у = 9х 5 имеют одинаковую четность (обе нечетные), а потому их произведение у = 9х 5 (5х 3 + 6х) является четным. С другой стороны, у = х 5 и у = х 8 + у 6 имеют различную четность, следовательно, их произведение у = х 5 (х 8 + у 6 ) нечетное.

Докажем справедливость этого правила. Пусть есть две ф-ции, у = у(х) и g = g(х), которые обладают какой-нибудь четностью. Определим четность их произведения у(х)•g(х). Для этого рассмотрим 3 различных случая:

Пример. Определите четность ф-ции у = (8х 4 + 3х 2 )(7х 5 + 2х)

Решение. Ф-ция из условия представляет собой произведение двух других ф-ций: у = 8х 4 + 3х 2 и у = 7х 5 + 2х. Первая из них является суммой двух четных и поэтому сама четная. Вторая ф-ция, наоборот, нечетная. Следовательно, их произведение – это тоже нечетная ф-ция.

Ответ: Нечетная ф-ция.

Пример. Определите четность ф-ции у = (х 6 + х 2 )(х 10 + х 8 )

Решение. Так как ф-ции у = х 6 + х 2 и у = х 10 + х 8 имеют одинаковую четность (обе четные), то их произведение является четным.

Для изучения следующего свойства ф-ций необходимо сначала рассмотреть понятие сложной ф-ции. Так называют ф-цию, которую получают подстановкой одной «простой» ф-ции в другую.Например, пусть есть ф-ции g = х 2 и у = х 3 + 2х. Подставив вторую в первую, получим

Ещё пример сложной ф-ции:

у = 2(9х 2 + 4х + 1) 3 + 3(9х 2 + 4х + 1)

Она получена путем подстановки выражения 9х 2 + 4х + 1 в ф-цию у = х 3 + 3х. В общем случае, если в ф-цию у = f (x) подставляют g(x), то используют запись у = f (g(x)). Иногда вместо термина «сложная функция» используют аналогичное понятие «композиция функций».

Итак, сформулируем ещё одно свойство четных функций:

которая будет четной. При этом природа ф-ции у = 5х + 7 + 1/х не играет никакой роли. Мы могли бы взять любую другую ф-цию, например, у = 958,235х 3 – 12,25х 2 + 19х + 2/3, и подставив в нее х 2 вместо х, получить ф-цию

у = 958,235(х 2 ) 3 – 12,25(х 2 ) 2 + 19х 2 + 2/3

которая будет четной.

Ограниченные и неограниченные функции

В математике говорят, что ф-ция у = х 2 ограничена снизу. То есть для любого допустимого х выполняется неравенство у(х) ⩾ а, где а – это какое-то произвольное число. И действительно, неравенство х 2 ⩾ 0 выполняется при всех значениях х. Также выполняются неравенства

Дадим определение функции, ограниченной снизу

Очевидно, что если неравенство у(х) ⩾ а выполняется хотя бы для одного числа а, то оно выполняется и для всех а, которые ещё меньше. Так, из справедливости неравенства х 2 ⩾ 0 автоматически следует справедливость неравенства х 2 ⩾ – 1,5, так как

Аналогично в математике существует понятие функции, ограниченной сверху.

В качестве примера ограниченной сверху ф-ции можно привести у = 4 – х 2 :

Ясно, что неравенство 4 – х 2 ⩽ 4 выполняется при всех х, то есть ни одна точка графика не лежит выше прямой у = 4.

Иногда бывает так, что функция ограничена одновременно и снизу, и сверху. Их называют ограниченными функциями.

Ф-ция, не попадающее под это определение, называется неограниченной функцией. В качестве примера неограниченной функции можно привести линейную ф-цию у = х + 1.

График ограниченной ф-ции находится в своеобразной «полосе» из горизонтальных линий, которые ограничивают его сверху и снизу. Примером ограниченной ф-ции является

С одной стороны, у этой дроби и числитель, и знаменатель – положительное число, поэтому она ограничена снизу прямой у = 0. С другой стороны, дробь тем больше, чем меньше ее знаменатель (если они оба положительны). Минимальное значение выражения х 2 + 1 – это единица (при х = 0), а поэтому максимальное значение дроби равно 4/1 = 4. Поэтому график ограничен сверху прямой у = 4.

Пример. Ограничена ли ф-ция

Решение. Выделим в ф-ции целую часть:

Так как величина 5х 2 + 5 всегда положительна, то и дробь

а значит, и вообще вся ф-ция положительна, то есть ограничена снизу прямой у = 0

С другой стороны, дробь будет принимать максимальное значение при минимальном значении знаменателя, которое равно 5 (при х = 0) При х = 0 имеем

Получается, что ф-ция ограничена сверху прямой у = 1,4.

Пример. Ограничена ли ф-ция

Решение. Величина х 2 всегда положительна, то есть х 2 ⩾ 0. Преобразуем это неравенство, умножив его на (– 1) и добавив к нему 16:

Получили, что подкоренное выражение не превосходит 16, а значит, и корень из него не больше, чем

То есть график будет ограничен прямой у = 4 сверху. С другой стороны, арифметический квадратный корень не может быть отрицательным числом, а потому его график ограничен снизу прямой у = 0. Для наглядности покажем график исследуемой ф-ции:

Квадратичная функция

В качестве ф-ции можно использовать квадратный трехчлен, например:

у = – 1,5х 2 + 19х + 0,5

у = 0,005х 2 + 654,25х – 124

Все эти ф-ции заданы с помощью выражения, представляющего собой квадратный трехчлен, поэтому в математике их называют квадратичными функциями.

Если коэффициент перед х 2 окажется равным нулю, то ф-ция превратится из квадратичной в линейную:

0х 2 + bx + c = bx + c

Попытаемся понять, как выглядит график квадратичной функции. Для этого начнем рассматривать частные случаи и использовать правило растяжения и сжатия, а также параллельного переноса графиков ф-ций.

Если в выражение для квадратичной ф-ции подставить значения

то получится уже известная нам степенная ф-ция у = х 2 :

Её графиком является парабола.

График ф-ции у = ах 2 – это тоже парабола (где а – некоторое число), которая однако, получена из «обычной» параболы у = х 2 путем сжатия или растяжения графика. Если коэффициент а является отрицательным, то парабола «перевернется» то есть отобразится симметрично относительно оси Ох. Покажем примеры нескольких графиков у = ах 2 :

Напомним, что при добавлении к ф-ции какого-нибудь постоянного числа n ее график переносится на n единиц вверх. Зная это можно легко получить график ф-ции у = ах 2 + с из графика у = ах 2 :

Таким образом, графиком ф-ции у = ах 2 + с является парабола, чья вершина поднята на с единиц вверх.

Как изменится график квадратичной ф-ции у = ах 2 + с, если в вместо х возводить в квадрат выражение (х +m), где m – произвольное число? В этом случае ф-ция примет вид у = а(х +m) 2 + с. Вершина параболы должна будет сместиться на m единиц влево:

Теперь докажем, что любая квадратичная ф-ция может быть представлена как в виде у = а(х + m) + n, где m и n – некоторые числа (в том числе и отрицательные). Похожие преобразования мы производили, когда учились решать квадратные уравнения. Запишем саму квадратичную ф-цию:

Вынесем множитель а за скобки:

Далее попытаемся преобразовать трехчлен в скобках, используя формулу квадрата суммы. Для этого добавим к нему и сразу же вычтем величину (b/2a) 2 :

Теперь раскроем внешние скобки:

Теперь произведем две замены:

Используя их, можно записать:

Получили, что любую квадратичную ф-цию можно свести к виду у = а(х + m) 2 + n. Что это значит и для чего мы это доказывали? Из этого факта следует, что график любой квадратичной ф-ции может быть получен из обычной параболы у = х 2 за счет трех действий.

Итак, как будет выглядеть график квадратичной ф-ции? В общем случае он является параболой, центр которой располагается не в точке (0;0), а в некоторой другой точке (х₀; у₀):

Если мы вернемся к доказательству того, что любую квадратичную ф-цию можно представить в виде у = а(х + m) 2 + n, то увидим, что число m рассчитывается по формуле

Так как график из-за этого числа m перемещается влево, а не вправо, то координата вершины х₀ рассчитывается по формуле:

Нет смысла составлять такую же формулу для определения координаты вершины у₀, ведь можно подставить х₀ в сам ф-цию и так узнать вторую координату вершины.

Пример. Определите вершину параболы, задаваемой ф-цией

у = 2х 2 + 8х + 5

Решение. Выпишем коэффициенты а, b и c квадратичной ф-ции:

Зная их, легко рассчитаем координату х вершины параболы:

Теперь подставим это число в исходную ф-цию и определим координату у вершины параболы:

у₀ = у(х₀) = 2(– 2) 2 + 8(– 2) + 5 = 8 – 16 + 5 = – 3

Напомним, что нули ф-ции – это те точки, в которых ее график пересекает ось Ох. Для их поиска необходимо приравнять ф-цию к нулю и решить уравнение. В случае с квадратичной ф-цией мы получим квадратной уравнение.

Пример. Постройте график ф-ции у = х 2 – 4х + 3, отметьте на нем вершину параболы и нули ф-ции.

Решение. Приравняем ф-цию к нулю:

Решим это уравнение

D = b 2 – 4ас = (– 4) 2 – 4•1•3 = 16 – 12 = 4

Итак, нашли нули ф-ции: 1 и 3. Теперь найдем вершину параболы:

у₀ = у(х₀) = 2 2 – 4•2 + 3 = 4 – 8 + 3 = – 1

Вершина находится в точке (2; – 1). Теперь отметим ее, а также нули ф-ции на графике, и соединим их линией, похожей на параболу:

При необходимости для точности построения всегда можно вычислить значение ф-ции в нескольких дополнительных точках и провести параболу через них. Здесь мы этого делать не будем

Ответ: вершина параболы – точка (2; – 1), нули ф-ции х₁ = 1 и х₂ = 3

Обратите внимание, что в рассмотренном примере вершина параболы оказалась ниже нулей, поэтому ее ветви смотрят вверх. Вообще, если коэффициент а > 0, то ветви смотрят вверх, а если а 2 – 4х + 6

у = – 3х 2 + 6х – 4

Решение. Начнем с первой ф-ции. Сначала найдем ее нули:

D = b 2 – 4ас = (– 4) 2 – 4•(– 2)•6 = 16+48 = 64

Найдем вершину. Сначала используем обычную формулу:

Далее просто проверим себя, найдя среднее арифметическое нулей ф-ции:

Как и ожидалось, получились одинаковые результаты! Вычислим теперь у₀:

у₀ = у(х₀) = – 2(– 1) 2 – 4(– 1) + 6 = – 2 + 4 + 6 = 8

Итак, вершина первой ф-ции – это точка (– 1; 8).

Перейдем ко второй ф-ции. Попробуем найти ее нули:

D = b 2 – 4ас = 6 2 – 4•(– 3)•(– 4) = 36–48 = – 16

Дискриминант отрицательный, значит, корней у уравнения нет. Не будет и нулей и ф-ции. Найдем вершину параболы

Найдем координату у₀ вершины:

у₀ = у(х₀) = – 3•1 2 + 6•1 – 4 = – 3 + 6 – 4 = – 1

Отметим, что у обоих графиков коэффициент а отрицательный, а потому их ветви будут смотреть вниз. Построим их графики:

Иногда приходится решать обратную задачу – по графику квадратичной ф-ции находить выражение, задающее эту ф-цию. Для ее решения необходимо подставлять в общий вид квадратичной ф-ции

значения квадратичной функции, взятые из графика (то есть координаты точек параболы) и получать уравнения, из которых можно найти величины a, b и c.

Пример. Запишите выражение для квадратичной ф-ции, имеющей следующий график:

Решение. Заметим, что графику параболы принадлежит точка с координатами (0; 3). Подставим эти числа, х = 0 и у = 3, в квадратичную ф-цию:

Итак, мы нашли, что коэффициент с = 3. Осталось найти а и b. Возьмем ещё одну точку, скажем, (1; 0), и подставим ее координаты (вообще в большинстве случаев удобно брать точки, одна из координат которой равна 0 или, на худой конец, единице):

Возьмем точку с координатами (– 3; 0):

Получили два уравнения с двумя неизвестными: a + b = – 3 и 9а – 3b = – 3. Решим систему, составленную из них:

Подставим первое уравнение во второе и получим:

Нашли а. Теперь подставим его в уравнение для b:

b = – 3 – а = – 3 – (– 1) = – 2

Получили b = – 2. Мы нашли все коэффициенты, а потому можем записать ф-цию в аналитическом виде:

Источник