Как доказать что граф не гамильтонов
05. Гамильтонов цикл и гамильтонов граф. Условия Дирака, Оре и Поша, гарантирующие существование в графе гамильтонова цикла
Пусть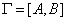 
— некоторый граф. Он называется Гамильтоновым, если в нем сущест-вует простой цикл, содержащий все вершины графа. Например, каждый полный граф – гамиль-тонов, потому что в нем проведены всевозможные ребра и, в частности, те, благодаря которым возможен обход по всем вершинам. А вот пример графа, не являющегося гамильтоновым:
Общих и легко осуществляемых действий, с помощью которых можно было бы достоверно выяснить, является ли данный граф гамильтоновым, не существует. Однако, имеются доста-точные условия на гамильтоновость, которые проверятются легко. Недостаток здесь состоит в том, что даже если ни одно из этих условий не выполняется, граф может оказаться гамильто-новым. В дальнейшем в этой лекции будет молчаливо предполагаться, что число вершин в лю-бом рассматриваемом графе не меньше трех.
Вот пример графа Дирака:
Вот пример графа Оре:
А вот пример графа, не являющегося графом Оре и, тем не менее, графа гамильтонова:
Нетрудно заметить, что всякий граф Дирака автоматически является графом Оре. Но вот пример графа Оре, не являющегося графом Дирака:
Для которого и строится функция 
:
;
Написанное означает, что функция 
в каждом целом неотрицательном 
принимает значение, равное количеству вершин графа , степень которых не превосходит . Такую функцию называют Функцией Поша графа .
Для примера построим функцию Поша следующего графа:
Молчание — золото: доказательство существования Гамильтонова цикла в графе
Заменив такую сложную конструкцию плоским графом, изоморфным исходному, получим задачу, которую далее рассмотрим в системе протоколов с нулевым разглашением.
Доказательство с нулевым разглашением
Очень убедительное (но не абсолютно определенное) свидетельство, что теорема верна, и что доказывающий знает это самое доказательство, дает интерактивный вероятностный протокол, называющийся доказательством с нулевым разглашением.
Интерактивность в данном определении говорит о том, что стороны общаются в течение нескольких раундов. В стандартных математических доказательствах имеет место только один вид взаимодействия: доказывающий дает проверяющему доказательство «на проверку», и на этом все заканчивается. В нашем же случае процесс доказательства утверждения превращается в разговор, который заканчивается убеждением проверяющего (если все идет хорошо).
Как убедить кого-то в существовании Гамильтонова цикла, не раскрывая сам цикл
Пусть обеим сторонам известен некоторый граф 
, вершины которого пронумерованы от 
до 
. Необходимо доказать проверяющему существование цикла в G, который посещает каждую вершину ровно один раз.
На вход системе с нулевым разглашением мы подаем
, где 
— положительное целое число, которое играет роль параметра безопасности и является количеством последовательных взаимодействий между сторонами: чем больше 
, тем больше уверенность проверяющего в доказательстве.
Дальнейшие шаги будут выполняться 
раз.
Доказывающая сторона выбирает случайную перестановку чисел 
и рисует матрицу смежности для графа, помечая строки и столбцы в соответствии с этой перестановкой. Получается новый граф, изоморфный исходному, построенный по данной матрице, если бы нумерация строк и столбцов у нее шла в естественном порядке.
Проще говоря, мы заменяем исходный граф на его изоморфную копию.
Приватное состояние матрицы, доступное только доказывающей стороне. Публичное состояние матрицы, известное обеим сторонам.
Проверяющая сторона получает скрытую матрицу и делает выбор:
Попросить доказывающую сторону открыть
сетки, соответствующих ребрам цикла Гамильтона. Процесс раскрытия симметричен: если показана запись 
в матрице, доказывающая сторона должна также показать запись
.
C другой стороны, можно попросить доказывающую сторону открыть граф целиком.
Результат для проверяющей стороны в первом случае будет выглядеть, например, так:
Наличие 1 во всех открытых квадратах говорит о существовании ребер между соответствующими вершинами графа. Так как мы открывали по условию те квадраты, которые отвечают ребрам цикла Гамильтона, получаем доказательство существования такого цикла в графе.
Если проверяющий имел бы возможность обращаться к доказывающему только с первой просьбой, последний мог бы его легко обмануть, и, не зная Гамильтонова цикла исходного графа G, мог бы подменить его на другой с тем же количеством вершин, в котором сам знал бы цикл. Короче говоря, проверяющий, прося показать весь граф целиком, хочет убедиться в том, что он действительно изоморфен исходному.
Выбор того, что проверяющий будет просить у доказывающего, на каждом шаге определяется «подбрасыванием монетки».
Если все в порядке, проверяющая сторона принимает доказательство.
Если же первом случае проверяющая сторона увидит в открытых квадратах 0, она поймет, что доказывающая сторона не владеет знанием о цикле Гамильтона. Аналогично, по описанной выше причине, проверяющая сторона во втором случае тоже может понять, что доказывающий пытается ее обмануть, и в итоге она отклонит доказательство.
Докажем, что проверяющая сторона, благодаря разговору, не может получить никакой «лишней» информации.
Может показаться, что в первом случае проверяющему предоставляется знание, благодаря которому он способен самостоятельно полностью узнать доказательство.
Это было бы верно, если бы он знал перестановку вершин, переводящую шифрованный граф в исходный, но поскольку за один раунд можно обратиться только с одной просьбой, и каждый раз изоморфная копия G меняется, то найти перестановку – дело безнадёжное – это значило бы решить проблему изоморфизма графов.
Что и требовалось доказать.
Заключение
Рассмотрим задачу аутентификации субъекта. Она состоит в проверке подлинности одной стороны другой, например, при входе в операционную систему пользователь может доказывать свою лигитимность вводом пароля.
Если решать ее таким простым способом, то гарантия того, что он не попадет в руки злоумышленников, не очень велика.
Конечно, при таком условии нельзя быть абсолютно уверенным в том, что аутентификация субъекта будет стопроцентной. Но проверяющий каждый раз может запросить любую часть информации, причём несколько раз. К тому же, можно использовать при этом Гамильтоновы циклы, получая относительно надёжную систему доступа, ведь вероятность в каждом раунде успешно обманывать проверяющую сторону равна 1/2^k, где k – число взаимодействий сторон.
Материал подготовлен при использовании литературы:
Manuel Blum «How to Prove a Theorem So No One Else Can Claim It«
Шнайер Б. Прикладная криптография, 2-е издание: протоколы, алгоритмы, исходные тексты на языке Си //Под редакцией ПВ Семьянова. М., Триумф. – 2002.
Теория графов в криптографии. Обзор основных подходов
Введение
Правильная раскраска графа в протоколах нулевого разглашения
Задача о правильной раскраске графа является одной известнейших проблем в области разметки графов. Формулируется она следующим образом: если дан граф
и количество цветов k (хроматическое число), то существует ли такая раскраска вершин графа G, при которой никакие две вершины, соединенные ребром, не были бы окрашены одним цветом?
Поиск хроматического числа, при котором данная задача разрешима, входит в класс NP-полных (т.е. решаемых не менее чем за полиномиальное время, что очень медленно). Более того, в данной работе было доказано, что при k=3 в случае планарного 4-регулярного графа доказать раскрашиваемость или ее отсутствие также можно не быстрее полиномиального времени. Поэтому даже 3-раскрашиваемость графа имеет большой интерес в криптографии и имеет практическое применение, к примеру, в протоколах нулевого разглашения.
Подробное описание задачи нулевого разглашения можно найти здесь. Если кратко, смысл заключается в доказательстве проверяющей стороне правильности утверждения без раскрытия самого алгоритма, с помощью которого ответ был получен. Идея протокола нулевого разглашения заключается в генерации последовательности итераций (сеансов связи), в результате каждой из которых контролер получает ответ на какой-либо вопрос. Этот вопрос не позволяет узнать решение задачи, но зато увеличивает вероятность того, что доказывающая сторона говорит правду. Завершением цикла является либо условие достижения некоторого количества последовательно верных ответов, либо получение ложного ответа, т.е. факт обмана.
Приведем пример. Пусть к студенту подходит школьник начальных классов и просит его решить квадратное уравнение. Из-за своего самолюбия, первый не желает раскрыть ребенку алгоритм нахождения дискриминанта, и потому просто диктует численный ответ. Но школьник хочет убедиться в том, что его не обманули. Тогда студент просит составить другое произвольное квадратное уравнение, чтобы повторить эксперимент. Если и в этот раз ребенок, подставив числа в выражение, получит тождество, то его степень доверия к человеку вырастет. Этот процесс генерации квадратных уравнений и его корней продолжается настолько долго, насколько требуется, чтобы убедить проверяющего в том, что источник достоверен. Важно отметить, что любой протокол нулевого разглашения должен удовлетворять трем свойствам:
Являться полным (порог доверия может быть задан сколь угодно близким к 100%).
Являться корректным (неправильный ответ приводит к потере доверия).
Иметь нулевое разглашение (проверяющий лишь убеждается в том, что ответы верные, но он ничего не узнает о том, как они получены).
Если алгоритм нахождения корней квадратного уравнения тривиален, то задача правильной раскраски графа NP-полна, потому ее решение для чрезмерно больших графов имеет коммерческую ценность. Предложим алгоритм нулевого разглашения на основе 3-раскрашиваемости с использованием распространенного протокола RSA.
Пусть доказывающая сторона, Алиса, знает правильную раскраску в три цвета
Планарный 4-регулярный граф с хроматическим числом k = 3
Для каждой вершины Алиса формирует случайное число r и заменяет в нем два младших бита на 00 (R), 01(G), 10(B) соответственно.
Для каждой вершины Алиса формирует параметры для RSA.
для каждой вершины посылает Бобу значения
Теперь Боб случайно выбирает в графе G одно ребро и сообщает Алисе данные об этом ребре. В ответ Алиса высылает два числа:
На основе которых Боб вычисляет цвета вершин, которые соединены выбранным ребром:
0,\ G=(V,E)» alt=»N=a|E|,\ a>0,\ G=(V,E)» src=»https://habrastorage.org/getpro/habr/upload_files/1cb/aa0/e67/1cbaa0e6776dd2f9e97f1fe2f7333fef.svg» width=»245″ height=»22″/>
Данный алгоритм удовлетворяет условию полноты. Вероятность того, что Алиса не разоблачена, составляет:
Важно отметить, что данный алгоритм удовлетворяет условию нулевого разглашения. Из-за того, что на каждой итерации цветовая палитра меняется, Боб, имея раскраску каждого ребра, не сможет подобно пазлу воссоздать правильную раскраску всего графа. Также нетрудно убедиться в том, что алгоритм является корректным.
Поиск гамильтонова цикла в графе
Если раскраска графа была иллюстрационным примером протокола нулевого разглашения, то задача поиска гамильтонова цикла лежит в основе его современной реализации.
Опишем идею алгоритма. Пусть Алиса знает гамильтонов цикл в графе Г и хочет доказать это Бобу (граф ему известен).
Алиса строит граф G, изоморфный графу Г. К примеру, она перенумеровывает вершины, сохраняя их первоначальные связи. Полученный граф представляется матрицей смежности H.
Матрица H шифруется в F, к примеру, по тому же алгоритму RSA:
и отправляется Бобу.
Получив матрицу F (зашифрованный граф G), Боб задает Алисе один из двух вопросов:
Какой гамильтонов цикл у графа G (а)?
Действительно ли G изоморфен Г (б)?
На вопрос (а) Алиса расшифровывает в F ребра, соответствующие гамильтонову циклу в G. На вопрос (b) Алиса расшифровывает граф G полностью, а также предоставляет перестановки, с помощью которых из Г получился G.
Получив ответ, Боб проверяет правильность расшифровки путем повторного шифрования Г и сравнения с F. Таким образом, он убеждается либо в корректности гамильтонова цикла в G, либо в изоморфности графов Г и G. Далее, если обмана зафиксировано не было, увеличить степень доверия и перейти к началу.
Отметим важные аспекты данного протокола. Во-первых, зачем Алисе строить изоморфный граф? Ответ: без этого Боб, получив ответ на вопрос (a), узнал бы гамильтонов цикл в исходом графе Г, что противоречит условию нулевого разглашения.
В-третьих, зачем Бобу задавать два вопроса, а не ограничиться лишь первым? В таком случае Алиса смогла бы сгенерировать свой собственный граф с уже имеющимся гамильтоновым циклом и, очевидно, Боб не обнаружит никаких противоречий в том, что гамильтонов цикл существует и корректен.
Вероятность обмана на t итерациях не превосходит
Доказательство простое и основано на том, что пара вопросов образует бинарное дерево исходов. Подробное доказательство того, почему данный протокол является протоколом нулевого разглашения, можно прочитать тут.
Графы как представление обобщённых клеточных автоматов
Поиск псевдослучайных функций является важной задачей криптографии. Они используются в блочных шифрах (AES) и алгоритмах хеширования (SHA-3). Существуют критерии качества псевдослучайных функций: выполнение строгого лавинного эффекта, анализ на коллизии, степень нелинейности и др. Они в той или иной степени оценивают близость функции к случайной, для чего существуют стандартизированные пакеты тестов (NIST statistical test suit).
Данный подход широко распространен, т.к. он имеет простую аппаратную реализацию. Классическим примером клеточного автомата, используемого в криптографии, является линейный конгруэнтный генератор псевдослучайных чисел на основе регистра сдвига.
ГПСЧ на основе регистра сдвига (период не максимальный)
Можно заметить, что модель клеточного автомата легко представима в виде графа. Его вершинами являются ячейки памяти с заданными локальными функциями связи, число аргументов которых определяется наличием или отсутствием ребер.
Граф ГПСЧ на регистре сдвига с точки зрения клеточного автомата
Таким образом, «качество» псевдослучайной функции в рамках рассматриваемой модели (клеточного автомата) будет определяться решением трех задач:
Как задать входные значения и номер итерации?
Какова структура графа обобщённого клеточного автомата?
Как задать локальные функции связи?
Подробные ответы на данные вопросы изложены здесь. В рамках заданной темы достаточно осветить второй пункт. Из соображений непредсказуемости и простоты аппаратной реализации граф должен удовлетворять следующим свойствам:
Быть приближенным к случайному (для псевдослучайности функции)
Иметь наименьший диаметр из теоретически возможных (для экономии аппаратных ресурсов)
Быть регулярным с минимальной степенью связности (для простоты задания локальных функций связи и повышения эффективности аппаратной реализации)
Не быть двудольным (для исключения быстрого рекурсивного разбиения на подграфы)
Быть масштабируемым на разное число ячеек памяти
есть максимальный по модулю, но не равный d, компонент спектра R. Чем же R отличаются от других?
то для минимизации h нужно брать вторую по величине компоненту спектра наиболее близкой к наибольшей. Это условие как раз хорошо выполняется в графах Рамануджана.
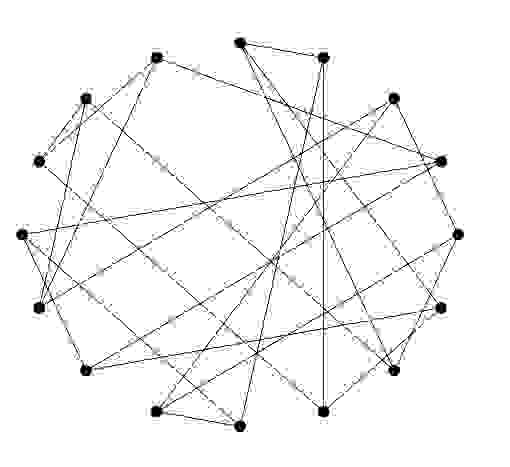
Сгенерировать случайный регулярный граф с заданным числом вершин.
Проверить граф на связность. Если он не связен, перейти к п.1.
Ниже приведен пример сгенерированного таким образом графа Рамануджана:
Randomly-generated 3-regular Ramanujan graph with N = 16 vertices
О графе состояний детерминированного генератора псевдослучайных чисел
Рассмотрим пример. Пусть с помощью ГПСЧ была получена последовательность чисел: <1, 5, 3, 3, 2, 4, 6, 2, 0, 4>. Тогда граф состояний будет выглядеть следующим образом:
Граф сосотояний ГПСЧ
Рассмотрим более практичный пример. Пусть дан простой детерминированный ГПСЧ, у которого каждое состояние имеет один образ (линейно конгруэнтный генератор, генератор на регистре сдвига, и др.). Пусть этих состояний всего 10 (от 0 до 9 включительно). При тестировании устройства была получена очень длинная последовательность псевдослучайных чисел, и после ее обработки построили граф состояний:
Граф состояний детерминированного ГПСЧ
Видно, что данный генератор отнюдь не идеальный: при максимальном периоде 10 на графе можно найти циклы длиной 5, 3 и даже 1. Граф самого безопасного ГПСЧ на десяти состояних должен был бы выглядеть так:
Граф состояний детерминированного ГПСЧ с максимально возможным периодом
Очевидно, что на практике число состояний детерминированного ГПСЧ делают очень большим. Это увеличивает вероятность того, что средняя длина цикла велика. В хороших ГПСЧ она достигает трехзначной степени двойки. Наличие циклов меньшей длины ухудшает его качество, т.к. может привести к полной детерминированности маленького и замкнутого множества состояний. Циклы в графе можно искать c помощью поиска в глубину с отслеживанием ранее проиндексированных вершин.
Заключение
Таким образом, в данной статье были рассмотрены базовые понятия и алгоритмы из теории графов, имеющие практическое применении в криптографии. Освещены такие понятия, как NP-полнота, нулевое разглашение и др. Приведено множество иллюстративных примеров (граф Рамануджана, ГПСЧ на регистре сдвига) и реализаций алгоритмов с ссылками на источники. Надеюсь, что данная статья будет полезной для любопытных читателей.
задан 8 Ноя ’20 1:12
Надо пояснить, что такое |G|, и что такое ||G||. Это не общепринятые обозначения, то есть их кто-то вводил, и при этом пояснял.
Также надо уточнить, какие графы рассматриваются (только простые, или не обязательно).
спасибо большое за замечание, исправил
@gg_math15: а тут на форуме нет службы личных сообщений. Что конкретно Вас интересует?
@gg_math15: так это и надо было там спросить, а не пытаться что-то скрыть или закрыть. Форум ведь и существует для обсуждений.
1 ответ
отвечен 8 Ноя ’20 11:19
@gg_math15: я бы советовал Вам начинать с того, что проверять каждое утверждение на истинность. У нас граф простой. Вершины v и w соединены ребром. Остальные рёбра или инцидентны v, или инцидентны w, или ни то, ни другое. То есть сказанное является правдой, причём очевидной правдой. Тогда она принимается, и читаем дальше. Если задумываться каждый раз над вопросом «зачем», то трудно будет дочитать до конца. И уже когда всё прочитано и понято, можно перечитывать и задавать вопросы такого уровня. Тогда станет ясно, для чего это говорилось: для вывода, что из v или w выходит мало удаляемых рёбер.
(продолжение) Назначение той фразы в том, что множество рёбер разделено на непересекающиеся части. Тогда, если в одной из них рёбер много, то в другой мало.
А почему в графе G’ останется больше f(n-1) рёбер? Ведь мы удаляли n-3 рёбра из графа Kn, а не из графа G на n вершинах. Кроме того, следует учитывать что рёбра графа G, инцидентные вершине v, также не вошли в G’, а их было больше n/2.
Наверное, нужно сказать, что в графе G с f(n) ребрами не более (n-2) рёбер инцидентно вершине v (так как одно ребро, инцидентное v и w, мы удалили), а значит, в графе G’ не менее f(n) рёбер.