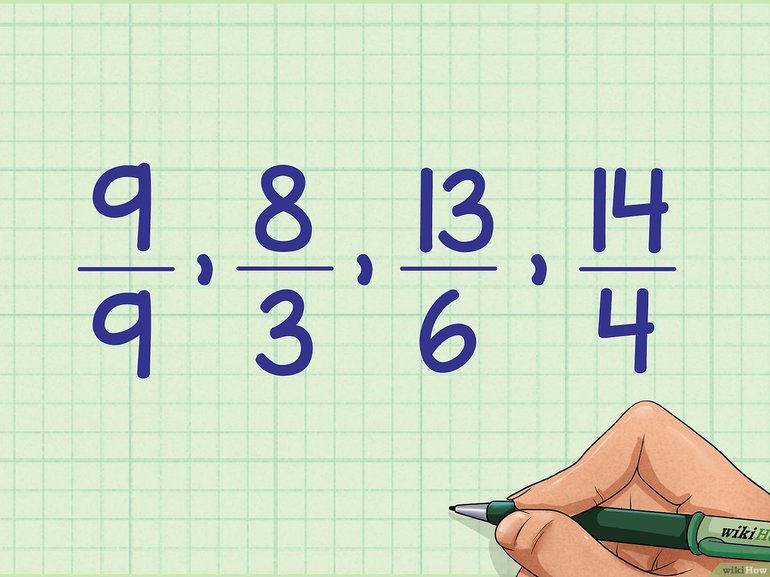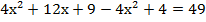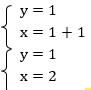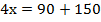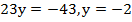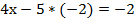Как доказать что кратно
Дроби с кратными от 1 до 5
На единицу делится любое целое число.
Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.
Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.
Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.
Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
Правило делимости на четыре звучит так: если две последние цифры номера кратны четырем либо оно в конце имеет два нуля, то отношение получится без остатка.
Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.
Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.
Свойства делителей от 6 до 10
Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.
Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.
Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.
Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:
Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.
В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:
Найти признак делимости на 8 очень легко. Формулировка закона такова: последние три цифры должны быть 000 или 888. Легко можно произвести вычисления с 789000: оно делится на 8, так как оканчивается на 000. Множество 289673888 тоже кратно 8, поскольку заканчивается на 888.
Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.
Разрядные единицы
Любое число можно разделить на разрядную единицу, если у него одинаковое или большее количество нулей в конце. Например, 5790 можно поделить на 10, так как в конце один ноль. Еще примеры:
Невозможно разделить 128700 на 1000, так как у разрядной единицы нулей больше, а также 237480 на 100 и другие подобные.
Делители от 11 и выше
Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.
Онлайн-задание с ответом: 7535, 74019 и 50486.
Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:
Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:
В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:
Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.
Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.
Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.
Например, 6942:
Еще пример — 754:
Признак делимости на составное число
Если делитель составной, необходимо его разложить на простые множители, которые не имеют общих кратных, кроме единицы. Пример: 15 раскладывается на 3 и 5. Любое неизвестное кратно 15, если одновременно кратно трем и пяти.
Также и с другим составным: 18 раскладывается на 2 и 9. Нельзя брать множители 3 и 6, так как они не простые, у них общее кратное 3. Например, 456 кратно трем, проверка: 4+5+6=15, также кратно 6 (при разложении на 2 и 3). Однако калькулятор выводит запятую. Если взять множители 2 и 9, будет видно, что двум — кратно, а девяти — нет, ведь сумма равна 15, которая не кратна 9.
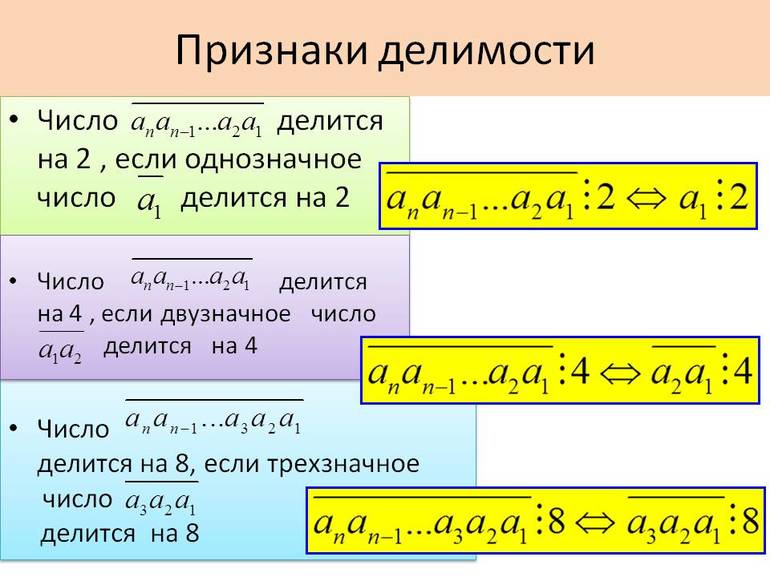
Таблица кратных от 2 до 10
Для удобства школьникам и их родителям предлагается таблица признаков делимости чисел от 2 до 10. Она наглядно и кратко демонстрирует всю вышеизложенную теоретическую часть:
| Делимость на: | Признак числа: |
| 2 | Оканчивается четной цифрой: 0, 2, 4,6, 8 |
| 3 | Сумма цифр, их которой оно состоит, делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Окончание на 5 или 0 |
| 6 | Одновременная кратность 2 и 3 |
| 8 | Три последние цифры кратны 8 |
| 9 | Сумма цифр кратна 3 |
| 10 | Окончание равно нулю |
Вышеизложенное доказывает, что к любому натуральному числу можно подобрать простой или составной признак кратности. На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.
Доказательство кратности и уравнение
Существует обратная задача – разложить многочлен на множители, она решается также с помощью формул сокращенного умножения.
Пример 6: доказать что число 
Очевидно, что если мы будем выполнять все вычисления, это будет сложно и долго, но если заметить формулу, то работа значительно упрощается. Итак, мы видим разность кубов. Распишем выражение:
В результате преобразований мы получили выражение, один из множителей которого равен 25, очевидно, что это выражение кратно 25.
Пример 7: решить уравнение:
Напомним, что решить уравнение – означает найти такие значения х, которые обращают выражение в верное числовое равенство. Распишем в уравнении квадрат суммы и разность квадратов:
Соберем неизвестные слева, а свободные члены справа и приведем подобные:
Из полученного элементарного уравнения найдем значение х:
Запишем еще несколько формул, которые можно вывести:
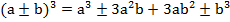
Чтобы вывести данные формулы, нужно выполнить умножение скобок, и вы убедитесь в их справедливости.
Итоги урока
Вывод: мы рассмотрели формулы сокращенного умножения, записали вид основных из них и некоторые доказали. Мы рассмотрели примеры различной сложности, чтобы окончательно закрепить данный материал.
1. Преобразовать выражение в многочлен:
а) (а – 2)(а + 2); б) (7а + 8в)²; в) (с³ – 0,1)².
2. Решить уравнение:
3. Упростить выражение и найдите его значение:
Урок 5:Повторение. Разложение многочленов на множители.
На данном уроке мы вспомним все изученные методы разложения многочлена на множители, рассмотрим примеры к ним.
1. Методы разложения многочленов на множители.
Напомним, что многочлен есть алгебраическая сумма одночленов, а одночлен – это произведение чисел и степеней.
Вспомним способы разложения многочлена на множители.
1. В каждом члене многочлена может быть общий множитель, отсюда первый способ – метод вынесения общего множителя за скобки, то есть такого множителя, который присутствует во всех членах многочлена. Рассмотрим пример 1, вынесем общий множитель за скобки, для этого определим, какие переменные представлены во всех членах, и вынесем их в минимальной степени:

Напомним, что, перемножив вынесенный множитель на скобку, можно проверить правильность вынесения.
В обоих членах есть скобка 
2. Метод группировки. Не всегда в многочлене можно вынести общий множитель. В таком случае нужно его члены разбить на группы таким образом, чтобы в каждой группе можно было вынести общий множитель, и постараться разбить так, чтобы после вынесения множителей в группах появился общий множитель у всего выражения, и можно было бы продолжить разложение. Рассмотрим пример 3:

Сгруппируем первый член со вторым, третий с четвертым и вынесем общие множители в группах:
У выражения появился общий множитель. Вынесем его:

3. Применение формул сокращенного умножения. Рассмотрим пример 4:
Мы расписали заданный многочлен по известной формуле разности кубов.
Комментарий: мы увидели в заданном многочлене формулу суммы кубов и разложили его.
4. Метод выделения полного квадрата. Он базируется на формулах квадрата суммы и квадрата разности. Напомним их:

Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Рассмотрим пример 6:

Итак, первое выражение – это 
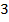
Свернем полный квадрат разности:

Преобразуем полученное выражение, применяя формулу разности квадратов, напомним, что разность квадратов двух выражений есть произведение суммы на их разность:

Напомним, что, перемножив скобки, можно проверить правильность разложения.
Подведение итогов урока
Вывод: мы вспомнили все изученные методы разложения многочленов на множители и рассмотрели примеры. Вспомнили определение и некоторые свойства алгебраических дробей, решили несколько типовых задач, с ними связанных.
1. Вынести общий множитель за скобки:
а) 8х – 8у; б) 5ху – 7х; в) 25х³ – 10х² + 5х;
2. Решить уравнение:
а) (7х – 10)(х + 5) = 0; б) 12у² – 60у = 0; в) х³ + х² – 4х – 4 = 0.
3. Докажите, что выражение:
а) 5¹³ – 5¹¹ делится на 24; б) 125³ + 625² делится на 6.
4. Разложите на множители способом группировки:
а) 3(а + с) + х(а + с); б) 6х – 6у + ах – ау;
Урок 6: Повторение. Системы двух линейных уравнений с двумя переменными.
1. Определение системы уравнений с двумя переменными
Напомним, что из себя представляет система двух линейных уравнений с двумя переменными. Это система вида:
Из первого уравнения 


Bторое линейное уравнение:



Запишем систему в другом виде:
Мы знаем, что множеством решений первого уравнения является множество точек, лежащих на соответствующей ему прямой, аналогично и для второго уравнения множество решений – это множество точек на другой прямой. Две прямые могут пересекаться – и тогда у системы будет единственное решение, единственная пара чисел х и у будет удовлетворять одновременно обоим уравнениям. Это происходит, если 




2. Способ подстановки
На данном уравнении можно продемонстрировать сразу несколько способов решения систем уравнений.
1 способ – способ подстановки: выразим во втором уравнении х и подставим полученное выражение в первое уравнение:
Подставим найденное значение у во второе уравнение и найдем значение х:
3. Способ алгебраического сложения
2 способ – способ алгебраического сложения: выполним сложение уравнений:
Из полученного уравнения найдем х:
Теперь вычтем из первого уравнения системы второе:
Таким образом, мы получили решение системы двумя способами, и это решение – точка с координатами (2; 1).
4. Системы уравнений с одним решением
В данном случае удобнее применить способ алгебраического сложения, вычтем из второго уравнения первое. Получаем:
Подставим значение у во второе уравнение и найдем х:
В данной системе нет переменных с одинаковыми коэффициентами, но мы можем их уравнять самостоятельно, для этого выполним преобразования:
Выполним сложение уравнений:
Подставим полученное значение у в первое уравнение и определим значение х:
5. Системы, имеющее бесконечное множество или не имеющие решений
Разделим второе уравнение на два:
Вычтем из первого уравнения второе:
Очевидно, что полученное выражение не зависит от значений переменных системы и не является верным числовым равенством, значит, система не имеет решений. В данном случае рекомендуется графически доказать, что система не имеет решений, для этого из уравнений записать линейные функции, построить их и показать, что прямые параллельны.
Очевидно, что, если разделить второе уравнение на два, получим первое уравнение:
Мы получили два одинаковых уравнения, значит, чтобы довести решение системы до конца, можем оставить одно: 

Графическая иллюстрация (рис. 1):
6. Подведение итогов урока
Вывод: мы рассмотрели системы двух линейных уравнений с двумя переменными, варианты и способы их решения. Мы вспомнили некоторые термины, понятия и свойства и решили примеры для закрепления техники.
1. Решите систему тремя способами: сложением, подстановки, графическим:
2. Сколько решений имеет система:
3. Решите систему любым способом:
Урок 7:Алгебраические дроби. Арифметические операции над алгебраическими дробями.Основные понятия.
На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется по 

1. Определение и примеры алгебраических дробей
Рациональные выражения делятся на целые и дробные выражения.
Определение.Рациональная дробь – дробное выражение вида 



Примерырациональных выражений: 



Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных 


Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.