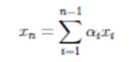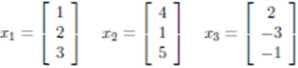Как доказать что матрица симметрична

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

kdnuggets

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:

Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

TimoElliott

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

Ортогональные матрицы

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

TimoElliott

Область значений и нуль-пространство матрицы

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают

Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx

), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

Собственные значения и собственные векторы

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

Источник

Symmetric Matrix

Then A′A is a p × p symmetric matrix and is decomposed as A′A = V Λ V′, where V is an orthogonal matrix whose columns are eigenvectors of A′A and Λ is a diagonal matrix whose diagonal elements are eigenvalues of A′A.

Related terms:

Vector and Matrix Operations for Multivariate Analysis

2.6.1 Symmetric Matrices

Figure 2.1 shows, in schematic form, various special matrices of interest to multivariate analysis. The first property for categorizing types of matrices concerns whether they are square (m = n) or rectangular. In turn, rectangular matrices can be either vertical (m > n) or horizontal (m

As we shall show in later chapters, square matrices play an important role in multivariate analysis. In particular, the notion of matrix symmetry is important. Earlier, a symmetric matrix was defined as a square matrix that satisfies the relation

That is, a symmetric matrix is a square matrix that is equal to its transpose. For example,

Symmetric matrices, such as correlation matrices and covariance matrices, are quite common in multivariate analysis, and we shall come across them repeatedly in later chapters. 7

A few properties related to symmetry in matrices are of interest to point out:

The product of any (not necessarily symmetric) matrix and its transpose is symmetric; that is, both AA′ and A′A are symmetric matrices.

If A is any square (not necessarily symmetric) matrix, then A + A′ is symmetric.

If A is symmetric and k is a scalar, then kA is a symmetric matrix.

The sum of any number of symmetric matrices is also symmetric.

The product of two symmetric matrices is not necessarily symmetric.

Later chapters will discuss still other characteristics of symmetric matrices and the special role that they play in such topics as matrix eigenstructures and quadratic forms.

Matrix Algebra

Spectral Decomposition

Any symmetric matrix A can be written as

where Λ is a diagonal matrix of eigenvalues of A and V is an orthogonal matrix whose column vectors are normalized eigenvectors. This decomposition is called as spectral decomposition.

For example, eigenvalues of a symmetric matrix

are 50 and 25. The corresponding eigenvectors are (4/5, 3/5)′ and (−3/5, 4/5)′. Then, A can be written as

If A is a nonsingular symmetric matrix, A r = VΛ r V′. If A is a nonsingular symmetric idempotent matrix, eigenvalues of A should be 0 or 1 since A 2 = A leads to Λ 2 = Λ.

Symmetric Matrix

A matrix S is symmetric if it equals its transpose. Real matrices of the form AA T and A T A are symmetric and have nonnegative eigenvalues.

Illustration

A symmetric matrix

A symmetric matrix of the form S.Transpose[S]

MatrixForm [R1 = S.Transpose[S]]

■ A symmetric matrix of the form Transpose[S].S

A symmetric matrix of the form (A + A T )

For every square matrix A, the matrix (A + A T ) is symmetric

SymmetricMatrixQ [A + Transpose [A]]

Elements of linear algebra

Theorem 2

A symmetric matrix A of order n is:

positive definite iff all the leading principal (upper-leftmost) minors are positive:

negative definite iff all the leading principal (upper-leftmost) minors alternate in sign, beginning with a negative minor;

positive semidefinite iff all the principal (not necessarily upper-leftmost) minors are ≥0, with the minor of order n equal to zero, i.e., |A| = 0;

negative semidefinite iff each one of the principal (not necessarily upper-leftmost) minors of even order is ≥ 0, each one of the principal (not necessarily upper-leftmost) minors of odd order is ≤ 0, with the minor of order n equal to zero, i.e., |A| = 0;

indefinite in all the other cases.

Let us see now how we can implement a quadratic form in Excel through the following example.

Krylov Subspace Methods

21.9 The Minres Method

If a symmetric matrix is indefinite, the CG method does not apply. The minimum residual method (MINRES) is designed to apply in this case. In the same fashion as we developed the GMRES algorithm using the Arnoldi iteration, Algorithm 21.8 implements the MINRES method using the Lanczos iteration. In the resulting least-squares problem, the coefficient matrix is tridiagonal, and we compute the QR decomposition using Givens rotations.

MINRES

function minresb(A,b,x₀,m,tol,maxiter)

% Solve Ax = b using the MINRES method

% Input: n × n matrix A, n × 1 vector b,

% initial approximation x₀, integer m ≤ n,

% error tolerance tol, and the maximum number of iterations, maxiter.

% Output: Approximate solution x_m, associated residual r,

% and iter, the number of iterations required.

% iter = −1 if the tolerance was not satisfied.

while iter ≤ maxiter do

Solve the (m + 1) × m least – squares problem T m ¯ y m = β e 1

using Givens rotations that take advantage of the tridiagonal

if r

end if

end while

end function

MINRES does well when a symmetric matrix is well conditioned. The tridiagonal structure of T_kmakes MINRES vulnerable to rounding errors [69, pp. 84-86], [72]. It has been shown that the rounding errors propagate to the approximate solution as the square of κ (A). For GMRES, the errors propagate as a function of the κ (A). Thus, if A is badly conditioned, try mpregmres.

Example 21.11

Convergence

Like GMRES, there is no simple set of properties that guarantee convergence. A theorem that specifies some conditions under which convergence will occur can be found in Ref. [73, pp. 50-51].

Remark 21.6

If A is positive definite, one normally uses CG or preconditioned CG. If A is symmetric indefinite and ill-conditioned, it is not safe to use a symmetric preconditioner K with MINRES if K −1 A is not symmetric. Finding a preconditioner for a symmetric indefinite matrix is difficult, and in this case the use of GMRES is recommended.

Congruent Symmetric Matrices

Two symmetric matrices A and B are said to be congruent if there exists an orthogonal matrix Q for which A = Q T BQ.

Illustration

Two congruent symmetric matrices

Q.Transpose [Q] == IdentityMatrix [2]

Congruence and quadratic forms

The previous calculations show that following two matrices are congruent:

Decomposition of Matrix Transformations: Eigenstructures and Quadratic Forms

5.6.4 Recapitulation

At this point we have covered quite a bit of ground regarding eigenstructures and matrix rank. In the case of nonsymmetric matrices in general, we noted that even if a (square) matrix A could be diagonalized via

the eigenvalues and eigenvectors need not be all real valued. (Fortunately, in the types of matrices encountered in multivariate analysis, we shall always be dealing with real-valued eigenvalues and eigenvectors.)

In the case of symmetric matrices, any such matrix A is diagonalizable, and orthogonally so, via

where T′ = T −1 since T is orthogonal. 13 Moreover, all eigenvalues and eigenvectors are necessarily real. If the eigenvalues are not all distinct, an orthogonal basis–albeit not a unique one–can still be constructed. Furthermore, eigenvectors associated with distinct eigenvalues are already orthogonal to begin with.

The rank of any matrix A, square or rectangular, can be found from its eigenstructure or that of its product moment matrices. If A_n×n is symmetric, we merely count up the number of nonzero eigenvalues k and note that r(A) = k ≤ n. If A is nonsymmetric or rectangular, we can find its minor (or major) product moment and then compute the eigenstructure. In this case, all eigenvalues are real and nonnegative. To find the rank of A, we simply count up the number of positive eigenvalues k and observe that r(A) = k ≤ min(m, n) if A is rectangular or r(A) = k ≤ n if A is square.

Finally, if A is of product-moment form to begin with, or if A is symmetric with nonnegative eigenvalues, then it can be written–although not uniquely so–as A = B′B. The lack of uniqueness of B was illustrated in the context of axis rotation in factor analysis.

Algorithmic Graph Theory and Perfect Graphs

2 Symmetric Matrices

all pivots are chosen along the main diagonal whose entries are each nonzero

correspond precisely to the perfect vertex elimination schemes of G(M). By Theorem 4.1 we obtain the equivalence of statements (ii) and (iii), first obtained by Rose [1970 ], in the following theorem. We present a generalization due to Golumbic [1978 ].

Theorem 12.1

Let M be a symmetric matrix with nonzero diagonal entries. The following conditions are equivalent:

M has a perfect elimination scheme;

M has a perfect elimination scheme under restriction (R);

G(M) is a triangulated graph.

Before proving the theorem, we must introduce a bipartite graph model of the elimination process. This model will be used here and throughout the chapter.

An edge e = xy of a bipartite graph H = (U, E) is bisimplicial if Adj(x) + Adj(y) induces a complete bipartite subgraph of H. Take note that the bisimpliciality of an edge is retained as a hereditary property in an induced subgraph. Let σ = [e₁, e₂, …, e_k] be a sequence of pairwise nonadjacent edges of H. Denote by S_i the set of endpoints of the edges e₁, …, e_i and let S₀ = ∅. We say that σ is a perfect edge elimination scheme for H if each edge e_i is bisimplicial in the remaining induced subgraph H U − S i − 1 and H U − S n has no edge. Thus, we regard the elimination of an edge as the removal of all edges adjacent to e. For example, the graph in Figure 12.5 has the perfect edge elimination scheme [x₁y₁, x₂y₂, x₃y₃, x₄y₄]. Notice that initially x₂y₂ is not bisimplicial. A subsequence σ′ = [e₁, e₂, …, e_k] of σ(k ≤ n) is called a partial scheme. The notations H – σ′ and H U − S k will be used to indicate the same subgraph.

Proof of Theorem 12.1

We have already remarked that (ii) and (iii) are equivalent, and since (ii) trivially implies (i), it suffices to prove that (i) implies (iii). Let us assume that M is symmetric with nonzero diagonal entries, and let σ be a perfect edge elimination scheme for B(M).

Corollary 12.2

A symmetric matrix with nonzero diagonal entries can be tested for possession of a perfect elimination scheme in time proportional to the number of nonzero entries.

Proof

Theorem 12.1 characterized perfect elimination for symmetric matrices. Moreover, it says that it suffices to consider only the diagonal entries. Haskins and Rose [1973 ] treat the nonsymmetric case under (R), and Kleitman [1974 ] settles some questions left open by Haskins and Rose. The unrestricted case was finally solved by Golumbic and Goss [1978 ], who introduced perfect elimination bipartite graphs. These graphs will be discussed in the next section. Additional background on these and other matrix elimination problems can be found in the following survey articles and their references: Tarjan [1976 ], George [1977 ], and Reid [1977 ]. A discussion of the complexity of algorithms which calculate minimal and minimum fill-in under (R) can be found in Ohtsuki [1976 ], Ohtsuki, Cheung, and Fujisawa [1976 ], Rose, Tarjan, and Lueker [1976 ], and Rose and Tarjan [1978 ].

Large Sparse Eigenvalue Problems

22.4 Eigenvalue Computation Using the Lanczos Process

As expected, a sparse symmetric matrix A has properties that will enable us to compute eigenvalues and eigenvectors more efficiently than we are able to do with a nonsymmetric sparse matrix. Also, much more is known about convergence properties for the eigenvalue computations. We begin with the following lemma and then use it to investigate approximate eigenpairs of A.

Lemma 22.1

Proof

Taking the norm of the equality and noting that the <p_i> are orthonormal, we obtain

Note that ∑ i = 1 n p i p i T = I (Problem 22.4). Let λ_k be the eigenvalue closest to θ, i.e., |λ_k − θ| ≤ |λ_i − θ| for all i, and we have

Recall that the Lanczos process for a symmetric matrix discussed in Section 21.8 is the Arnoldi process for a symmetric matrix and takes the form

It follows from Lemma 22.1 that there is an eigenvalue λ such that

Example 22.5

The very ill-conditioned (approximate condition number 2.5538×10 17 ) symmetric 60000×60000 matrix Andrews obtained from the Florida sparse matrix collection was used in a computer graphics/vision problem. As we know, even though the matrix is ill-conditioned, its eigenvalues are well conditioned ( Theorem 19.2 ). The MATLAB statements time the approximation of the six largest eigenvalues and corresponding eigenvectors using eigsymb. A call to residchk outputs the residuals.

〉〉 tic;[V, D] = eigssymb(Andrews, 6, 50);toc;

Elapsed time is 5.494509 seconds.

Eigenpair 1 residual = 3.59008e-08

Eigenpair 2 residual = 1.86217e-08

Eigenpair 3 residual = 2.31836e-08

Eigenpair 4 residual = 7.68169e-08

Eigenpair 5 residual = 4.10453e-08

Eigenpair 6 residual = 6.04127e-07

22.4.1 Mathematically Provable Properties

This section presents some theoretical properties that shed light on the use and convergence properties of the Lanczos method.

In Ref. [76, p. 245], Scott proves the following theorem:

Theorem 22.1

This theorem says that if the spectrum of A is such that δ_A/4 is larger than some given convergence tolerance, then there exist poor starting vectors which delay convergence until the nth step. Thus, the starting vector is a critical component in the performance of the algorithm. If a good starting vector is not known, then use a random vector. We have used this approach in our implementation of eigssymb.

The expository paper by Meurant and Stratkos [70, Theorem 4.3, p. 504] supports the conclusion that orthogonality can be lost only in the direction of converged Ritz vectors. This result allows the development of sophisticated methods for maintaining orthogonality such as selective reorthogonalization [2, pp. 565-566], [6, pp. 116-123].

There are significant results concerning the rate of convergence of the Lanczos algorithm. Kaniel [77] began investigating these problems. Subsequently, the finite precision behavior of the Lanczos algorithm was analyzed in great depth by Chris Paige in his Ph.D. thesis [78]; see also Paige [79–81]. He described the effects of rounding errors in the Lanczos algorithm using rigorous and elegant mathematical theory. The results are beyond the scope of this book, so we will assume exact arithmetic in the following result concerning convergence proved in Saad [3, pp. 147-150].

Theorem 22.2

Let A be an n-by-n symmetric matrix. The difference between the ith exact and approximate eigenvalues λ_i and λ i ( m ) satisfies the double inequality

Remark 22.3

Error bounds indicate that for many matrices and for relatively small m, several of the largest or smallest of the eigenvalues of A are well approximated by eigenvalues of the corresponding Lanczos matrices. In practice, it is not always the case that both ends of the spectrum of a symmetric matrix are approximated accurately. However, it is generally true that at least one end of the spectrum is approximated well.

Least-Squares Problems

16.2.1 Using the Normal Equations

Find the Cholesky decomposition A T A = R T R.

Solve the system R T y = A T b using forward substitution.

Solve the system Rx = y using back substitution.

Example 16.4.

There are three mountains m₁, m₂, m₃ that from one site have been measured as 2474 ft., 3882 ft., and 4834 ft. But from m₁, m₂ looks 1422 ft. taller and m₃ looks 2354 ft. taller, and from m₂, m₃ looks 950 ft. taller. This data gives rise to an overdetermined set of linear equations for the height of each mountain.

In matrix form, the least-squares problem is

A T A = [ 3 − 1 − 1 − 1 3 − 1 − 1 − 1 3 ] has the Cholesky decomposition

[ 1.7321 − 0.5774 − 0.5774 0 1.6330 − 0.8165 0 0 1.4142 ] x = y

Algorithm 16.1 uses the normal equations to solve the least-squares problem.

Least-Squares Solution Using the Normal Equations

% Solve the overdetermined least-squares problem using the normal equations.

% Input: m × n full-rank matrix A, m ≥ n and an m × 1 column vector b.

% Output: the unique least-squares solution to Ax = b and the residual

Use the Cholesky decomposition to obtain A T A = R T R

Solve the lower triangular system R T y = c

Solve the upper triangular system Rx = y

return [ x ‖ b − A x ‖ 2 ]

NLALIB: The function normalsolve implements Algorithm 16.1 by using the functions cholesky and cholsolve.

The efficiency analysis is straightforward.

Cholesky decomposition of A T A : n 3 3 + n 2 + 5 n 3 flops

Forward and back substitution: 2 ( n 2 + n − 1 ) flops

The total is n 2 ( 2 m + n 3 ) + 2 m n + 3 n 2 + 11 3 n − 2 ≃ n 2 ( 2 m + n 3 ) flops

There may be some loss of significant digits when computing A T A. It may even be singular to working precision.

We will see in Section 16.3 that the accuracy of the solution using the normal equations depends on the square of condition number of the matrix. If κ (A) is large, the results can be seriously in error.

Источник