Как доказать что окружность вписанная
Вписанная окружность
Теорема
| В любой треугольник можно вписать окружность. |
Доказательство
Дано: произвольный 
АВС.
Доказать: в АВС можно вписать окружность.
Доказательство:
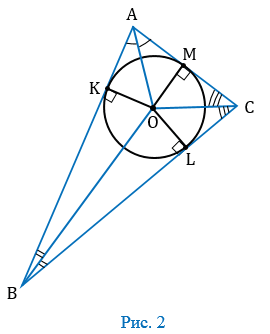
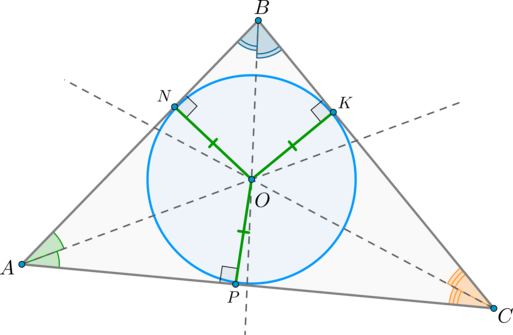
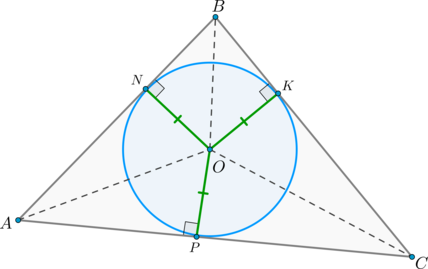
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).
2. Точка О равноудалена от сторон АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в АВС. Теорема доказана.
Замечание 1
| В треугольник можно вписать только одну окружность. |
Доказательство
Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.
Замечание 2
| Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. |
Доказательство
Замечание 3
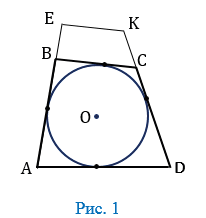
| Не во всякий четырехугольник можно вписать окружность. |
Доказательство
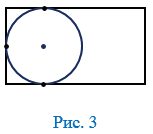
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон (Рис.3), но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.
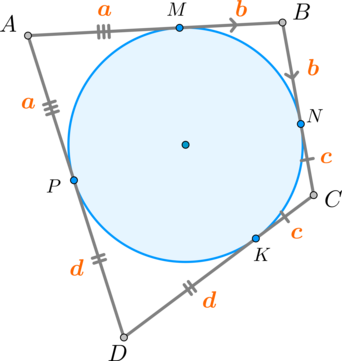
Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
| В любом описанном четырехугольнике суммы противоположных сторон равны. |
Доказательство
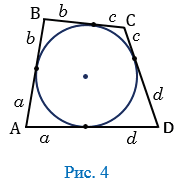
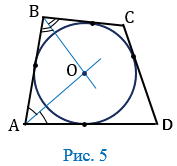
Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD =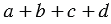 
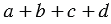
и ВС + АD = , следовательно, АВ + СD = ВС + АD.
Верно и обратное утверждение:
| Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. |
Доказательство
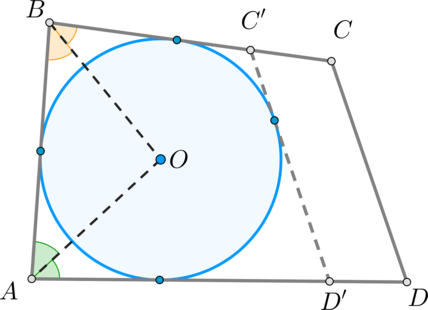
Пусть в выпуклом четырехугольнике АВСD
АВ + СD = ВС + АD. (1)
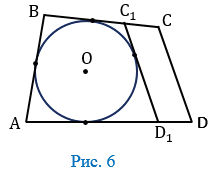
Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).
Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.
АВ + С1D1 = ВС1 + AD1. (2)
Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству
т.е. в четырехугольник С1СDD1 одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. к аждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Вписанная окружность (ЕГЭ 2022)
Ну что, юнга, уверен, что знаешь все про окружности?
Пров вписанную точно знаешь. А про вневписанную слышал?
Ничего страшного, сейчас ты во всём разберешься!
Вписанная окружность — коротко о главном
Вписанная в треугольник окружность — окружность, которая касается всех (трёх) сторон треугольника.
В любой треугольник можно вписать окружность, причём единственным образом.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Отрезки от вершин треугольника до точек касания выражаются по формулам:
Площадь треугольника через радиус вписанной окружности:
\( \displaystyle S=p\cdot r\), где \( \displaystyle p=\frac
Вневписанная окружность – окружность, которая касается одной стороны треугольника и продолжений двух других сторон.
Центр вневписанной окружности лежит на пересечении биссектрисы внутреннего угла треугольника (\( \displaystyle \angle A\)) и биссектрис двух внешних углов (\( \displaystyle \angle B\) и \( \displaystyle \angle C\)).
Площадь треугольника через радиус вневписанной окружности:
\( \displaystyle <_<\Delta ABC>>=(p-a)\cdot r\), где \( \displaystyle p=\frac
Вписанная окружность — подробнее
Здесь мы будем говорить об окружностях, связанных с треугольником. Оставим пока в стороне страшное слово «вневписанная» и поговорим об окружности, вписанной в треугольник.
Итак, что же это такое?
Окружность называется вписанной в треугольник, если она касается всех(трёх) его сторон.
Для всякого ли треугольника можно подобрать такую окружность? И как найти ее центр?
На эти вопросы отвечает следующая теорема:
Во всякий треугольник можно вписать окружность, причём единственным образом.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
И повторим ещё раз то, что очень нужно запомнить:
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Если тебя заинтересовал вопрос о том, почему это все три биссектрисы обязаны пересечься, и какое отношение имеют биссектрисы к тому, что окружность касается сторон треугольника, то добро пожаловать к теме «Биссектриса».
Но для начала хватит просто запомнить то, что центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Теперь немножко о радиусе.
Радиус вписанной окружности
Посмотри, пусть у нас в \( \displaystyle \Delta ABC\) вписана окружность с центром \( \displaystyle O\).
Тогда отрезки \( \displaystyle OK\), \( \displaystyle OL\), и \( \displaystyle OM\) – радиусы этой окружности.
Поэтому они, конечно же, равны, но ещё – они все перпендикулярны сторонам. Это происходит оттого, что радиус, проведенный в точку касания, перпендикулярен касательной.
Итак, запомни и используй:
Вписанная окружность и отрезки сторон треугольника
Давай представим, что мы откуда-то узнали все три стороны треугольника.
Можно ли найти как-то отрезочки \( \displaystyle AK\), \( \displaystyle KC\), \( \displaystyle BL\) и.д. —отрезки, на которые точки касания разбивают стороны треугольника?
Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).
Посмотри внимательно: из точки \( \displaystyle A\) проведено две касательных, значит их отрезки \( \displaystyle AK\) и \( \displaystyle AM\) равны.
Мы обозначим их «\( \displaystyle x\)».
Далее, точно так же:
\( \displaystyle BM=BL=y\) (обозначили).
\( \displaystyle CK=CL=z\) (обозначили).
Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины «\( \displaystyle a\)», «\( \displaystyle b\)», «\( \displaystyle c\)» — смотри на рисунок. Что же теперь получилось?
А вот, например, отрезок «\( \displaystyle a\)» состоит из двух отрезков «\( \displaystyle y\)» и «\( \displaystyle z\)», да и отрезки «\( \displaystyle b\)» и «\( \displaystyle c\)» тоже из чего-то состоят. Запишем это всё сразу:
Ух ты! Выход в алгебру! Три уравнения и три неизвестных! Сейчас решим!
Сложим первые два уравнения и вычтем третье:
\( \displaystyle \left\< \begin
А теперь сложим первое и третье уравнение и вычтем второе:
\( \displaystyle \left\< \begin
И последний шаг: сложим второе и третье, а потом вычтем первое.
Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.
Секрет вот в чём: те стороны, на которых есть «\( \displaystyle x\)» («\( \displaystyle b\)» и «\( \displaystyle c\)») будут с плюсом, а та сторона, где нет «\( \displaystyle x\)» (это «\( \displaystyle a\)»), будет с минусом.
Ну, а пополам поделить всё хозяйство. С другими буквами точно так же
На «\( \displaystyle a\)» и «\( \displaystyle c\)» есть «\( \displaystyle y\)» — они с плюсом, на «\( \displaystyle b\)» нет «\( \displaystyle y\)» — она с минусом
На «\( \displaystyle a\)» и «\( \displaystyle b\)» есть «\( \displaystyle z\)» — они с плюсом, на «\( \displaystyle c\)» нет «\( \displaystyle z\)» — она с минусом.
Вписанная окружность и площадь
Здесь скажем совсем коротко:
Есть такая формула:
\( \huge\displaystyle S=p\cdot r\),
где \( \displaystyle p\) — это полупериметр треугольника, то есть \( \displaystyle p=\frac
Вневписанная окружность
Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:
Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.
Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон.
А как ты думаешь, сколько у одного треугольника может быть вневписанных окружностей? Вот, представь себе, аж три!
Захватывает дух? Насладись впечатлением.
А еще подумай над тем…
А сейчас вернёмся к одной какой-нибудь вневписанной окружности и узнаем всего один, но очень важный факт:
До дальней точки касания вневписанной окружности ровно полупериметр
или что то же самое: \( \displaystyle AK=AM=p\), где \( \displaystyle p\) — полупериметр.
Доказывать не будем, но ещё раз посмотри и запомни:
До «дальней» точки касания вневписанной окружности – ровно полупериметр треугольника.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Слово лучшему ученику — тебе! 🙂
Навыки работы с окружностями показывают, насколько ты хорош в планиметрии. Это действительно сложная тема.
А сегодня ты с ней разобрался. Ты большой молодец!
Мы будем очень рады узнать твое мнение об этой статье. Для нас оно очень важно.
Напиши внизу в комментариях, что думаешь об этой статье. Помогла ли она тебе?
Нравится ли тебе работать с окружностями? И стало ли это делать легче после прочтения этой статьи? 🙂
Остались вопросы? Задай их! Там же, в комментариях.
Мы обязательно ответим тебе!
Добавить комментарий Отменить ответ
Один комментарий
Некоторые комментарии прошлых лет к этой статье:
Андрей
11 июля 2018
Прекрасное обьяснение, спасибо большое!
Александр (админ)
12 июля 2018
И тебе спасибо, Андрей. За теплые слова.
Юлия
09 сентября 2018
все просто и понятно, спасибо большое!
Александр (админ)
09 сентября 2018
И тебе спасибо, Юлия! Очень приятно слышать!
Миша
28 сентября 2018
не подскажите, почему отрезок о3б перпендикулярен отрезку о1о2?
Александр
21 августа 2019
Это биссектрисы смежных углов.
Денис
24 февраля 2019
Божественные рисунки!) Мне в школе для урока по геометрии надо подготовить несколько рисунков. Подскажите, пожалуйста, какой программой вы пользуетесь для построения рисунков?
Александр (админ)
07 марта 2019
Денис, прошу прощения, пост твой пропустил. Только сейчас отвечаю. Но врядли чем-то помогу. Рисунки делались так: сначала их от руки делала Елена Евгеньевна (наш математик), а потом профессиональный дизайнер Настя их перерисовывала. По-моему в фотошопе.
Окружность: вписанная в многоугольник или угол
Определения
В этом случае многоугольник \(P\) называется описанным около окружности.
Теорема
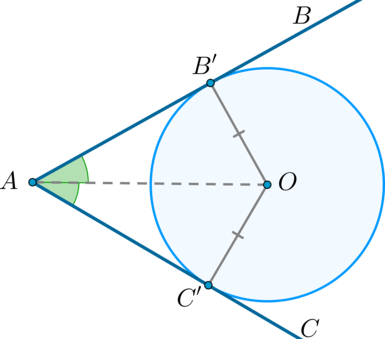
Центр вписанной в угол окружности лежит на его биссектрисе.
Доказательство
Теорема
В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.
Доказательство
Данная окружность единственна, т.к. если предположить, что существует другая вписанная в \(\triangle ABC\) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.
Таким образом, попутно была доказана следующая теорема:
Следствие
Биссектрисы треугольника пересекаются в одной точке.
Теорема о площади описанного треугольника
Если \(a,b,c\) – стороны треугольника, а \(r\) – радиус вписанной в него окружности, то площадь треугольника \[S_<\triangle>=p\cdot r\] где \(p=\dfrac
Доказательство
Но \(ON=OK=OP=r\) – радиусы вписанной окружности, следовательно,
Следствие
Если в многоугольник вписана окружность и \(r\) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на \(r\) : \[S_<\text<опис.мног-к>>=p\cdot r\]
Теорема
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство
Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Предположим, что это не так. Тогда \(CD\) либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).
\[AB+C’D’=BC-CC’+AD-DD’ \Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD\]
Получили, что в четырехугольнике \(C’CDD’\) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, \(CD\) касается окружности.
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.
Теоремы
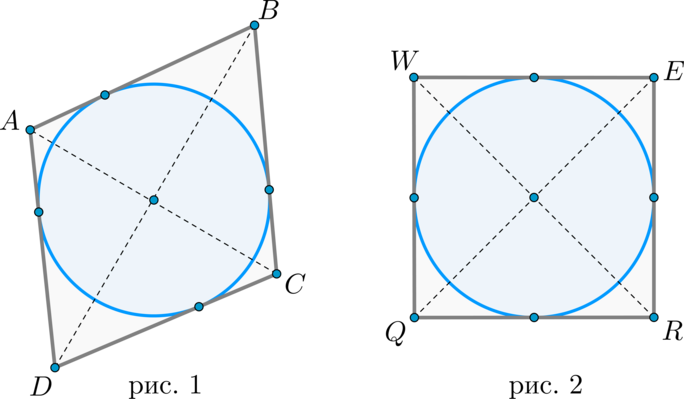
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.
Доказательство
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.
Окружность, вписанная в треугольник. Теоремы и их рассмотрение
Вам будет интересно: Казахская академия спорта и туризма. Факультеты, структура вуза
Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:
В треугольник можно вписать только одну окружность.
Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:
Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.
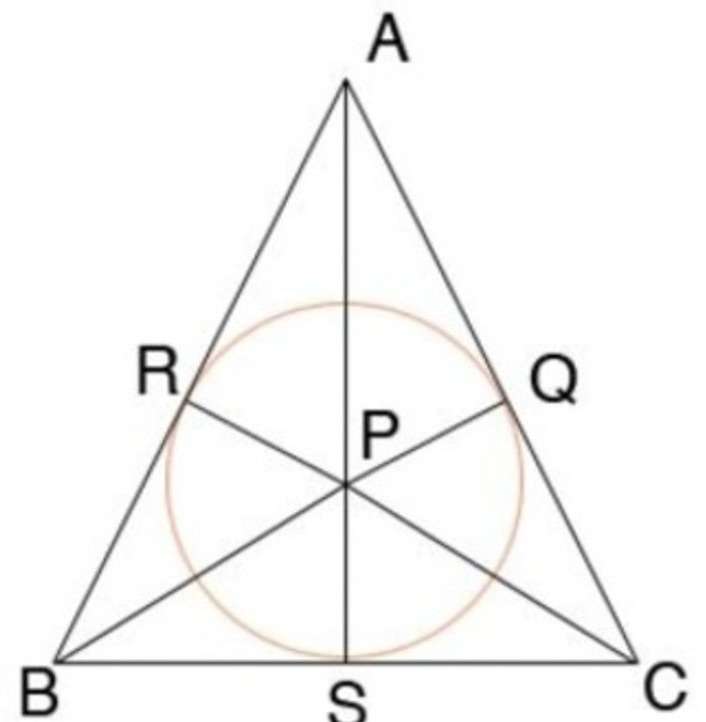
Окружность, вписанная в равнобедренный треугольник
Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.
Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).
Свойства теоремы об окружности, вписанной в треугольник:
Окружность, вписанная в прямоугольный треугольник
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.
Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.
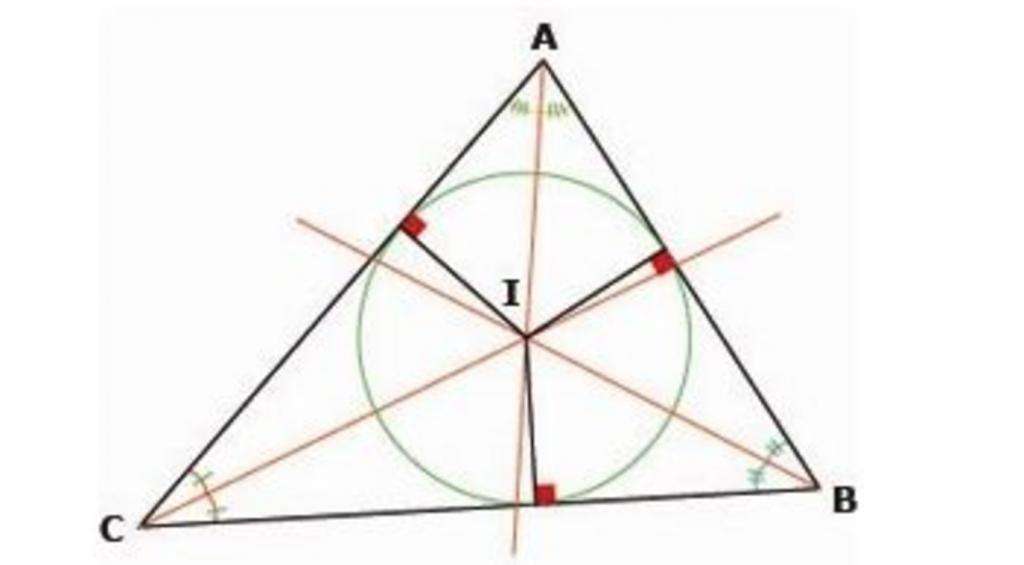
Формулировка теоремы о вписанной окружности
В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.
Теорема о центре окружности, вписанной в треугольник
Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.
Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.