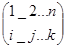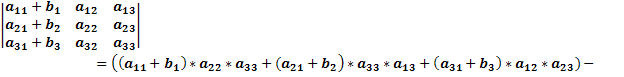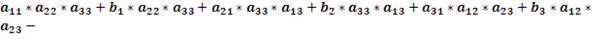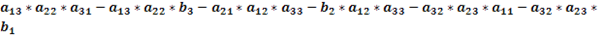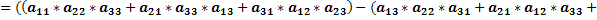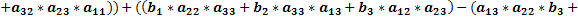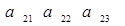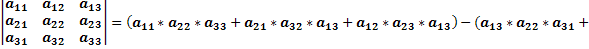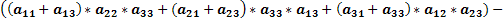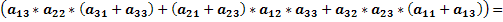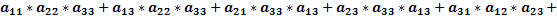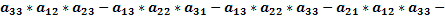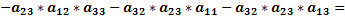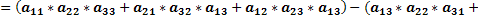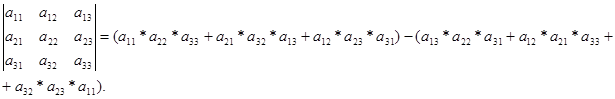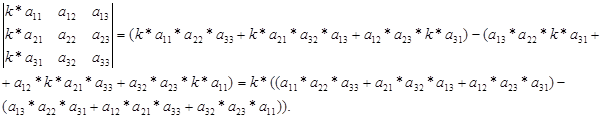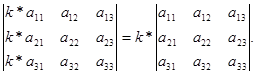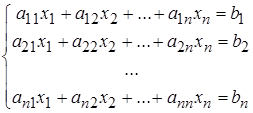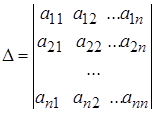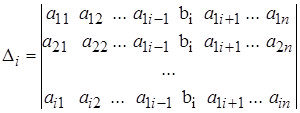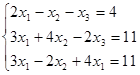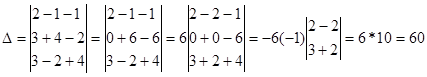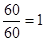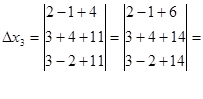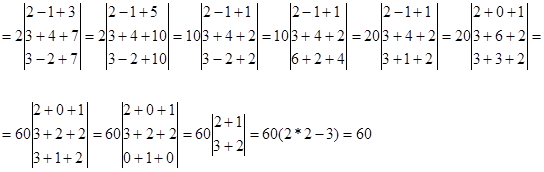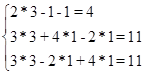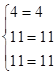Как доказать что определитель матрицы делится на число

Линейная алгебра: Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Открыта свободная публикация вакансий для математиков	26.09.2019 16:34
	Актуарий в PPF Life Insurance (Junior)	25.03.2021 21:35
	Разделу «Задачки и головоломки» исполнилось два года	21.08.2021 01:51

Помогите решить пожалуйста:
Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Доказать, почему det матрицы :
1 0 8 1
1 4 0 3
2 0 9 3
1 5 4 1
делится на 23 тоже.

Редактировалось 2 раз(а). Последний 12.11.2009 20:23.

помогите ещё: каким способом легче всего вычислить детерминант симметрической матрицы типа:

$\left(\begin x_1 & a & b \\ a & x_2 & c \\ b & c & x_3 \end\right)$

Редактировалось 3 раз(а). Последний 12.11.2009 21:02.

Редактировалось 1 раз(а). Последний 12.11.2009 21:02.

Цитата
sidi98765
Помогите решить пожалуйста:
Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Доказать, почему det матрицы :
1 0 8 1
1 4 0 3
2 0 9 3
1 5 4 1
делится на 23 тоже.

Редактировалось 1 раз(а). Последний 12.11.2009 21:03.

Цитата
sidi98765
Помогите решить пожалуйста:
Даны числа 1081, 1403, 2093, 1541, которые делятся на 23.

Доказать, почему det матрицы :
1 0 8 1
1 4 0 3
2 0 9 3
1 5 4 1
делится на 23 тоже.

Ее определитель будет равен произведению собственных значений. Поэтому, если Вы умеете простым способом найти собственные значения, то и определитель мгновенно сыщется.

Редактировалось 1 раз(а). Последний 13.11.2009 11:04.

Источник

Доказательства свойств определителя

Свойство №1: Определитель не изменяется при транспортировании матриц (строк и столбцов).

Доказательство:

Опр. Матрицы A_ji называется транспонированной матрицей A_ij

= det A = det A T

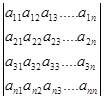
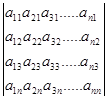
Выберем любое слагаемое из суммы определителя.

Следовательно определители равны.

Свойство №2: Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.

Доказательство:

Пусть дана матрица, один столбец которой равен 0.

=detA подсчитаем определитель данной матрицы.

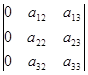
Подсчитаем определитель данной матрицы, используя правило равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям.

=0*а₂₂*а₃₃+а₁₂*а₂₃*0+а₃₂*а₁₃*0 = 0

=-(а₁₃*а₂₂*0+а₁₂*а₃₃*0+а₂₃*а₃₂*0)=0

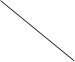
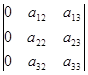
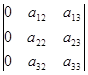
Свойство №3: Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.

Доказательство:Возьмём матрицу определитель которой равен detA и переставим в ней 2 столбца. Получим:

,после перестановки получим: .

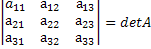
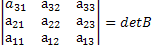
Посчитаем определители обеих матриц. Получим:

Получили, что det A=-det B.

Свойство №4: Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.

Доказательство:

Возьмём матрицу, в которой элементы первого столбца равны a_ij+b_j и посчитаем её определитель.

.

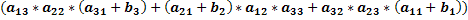
Раскроем скобки и приведём подобные слагаемые.

.

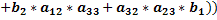
То есть: .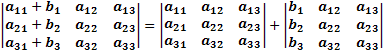

Свойство №5: Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.

Доказательство:

Пусть дан определитель detA≠0, содержащий две равные строки.

= detA ; =

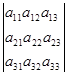
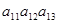
Поменяем местами эти равные строки. Получим новый определитель.

.

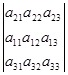
Так как данный определитель получен из определителя detA перестановкой строк, то из предыдущего свойства следует, что полученный определитель принимает значение –detA. В то же время, количество слагаемых и модуль значений определителей detA и –detA равны, то справедливо будет равенство detA=-detA. Из данного равенства следует что detA=0. Свойство доказано.

Свойство №6: Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).

Доказательство:

Возьмём матрицу коэффициентов и посчитаем её определитель.

Прибавим к первому столбцу третий. Получим новую матрицу.

.

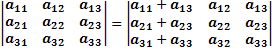
Посчитаем её определитель.

.

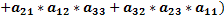
Свойство №7: Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.

Доказательство:Возьмём матрицу и посчитаем её определитель.

То есть.

5. Пример применения правила Крамера для решения систем n уравнений с n неизвестными

Определители очень широко используются при решении и исследовании систем линейных n уравнений с n неизвестными. Правило решения такой системы с помощью определителей называется правилом Крамера. Покажем это правило на примере.

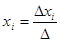
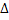
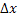
Правило Крамера: правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных , где — определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а _I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.

Пусть дана система из трех уравнений с тремя неизвестными:

Посчитаем определитель матрицы системы, составленной из коэффициентов при неизвестных:

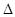
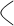
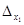
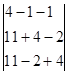
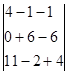
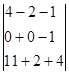
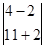
После подсчета определителя системы, подсчитаем определители неизвестных. Для этого вырезаем из столбец данной переменной, а на его место ставим столбец свободного члена.

= = = 6 = 6 = 6*(4*2-(-2)*11)=180

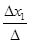
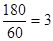
Согласно правилу Крамера значение неизвестной переменной равно частному от определителя данной неизвестной и определителя системы. Значит переменная x_{1= ;} x₁= .

Действуя по тому же алгоритму, найдем значения переменных x₂ и x₃:

По правилу равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям матрицы получим:

= 2*11*4+3*11*(-1)+4*(-2)*3= 88-33-24=31 =60

-2*(-2)*11-3*4*4 – (-1)*11*3= 44-48+33=29

Значит x₂=

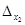
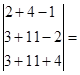
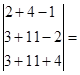
Значит x₃=

Для доказательства истинности правила Крамера, проверим полученные значения переменных, подставив полученные значения в систему:

После подстановки мы получили верное числовое равенство, значит, правило Крамера истинно для решения системы n уравнений с n неизвестными. Ответ: (3;1;1)

Глава 2.Векторное произведение

Источник