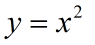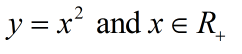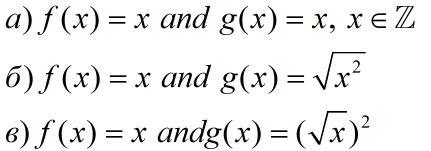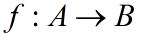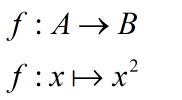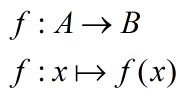Как доказать что отображение инъекция
Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения
Содержание:
Сюръекция, инъекция и биекция
По этой ссылке вы найдёте полный курс лекций по математике:
Правило, задающее отображение f: X (или функцию /), можно условно изобразить стрелками (рис. 2.1). Бели в множестве У есть хотя бы один элемент) на который не указывает ни одна из стрелок, то это свидетельствует о том, что область значений функции f не заполняет все множество У, т.е. f(X) С У. Если же область значений / совпадает с У, т.е. f
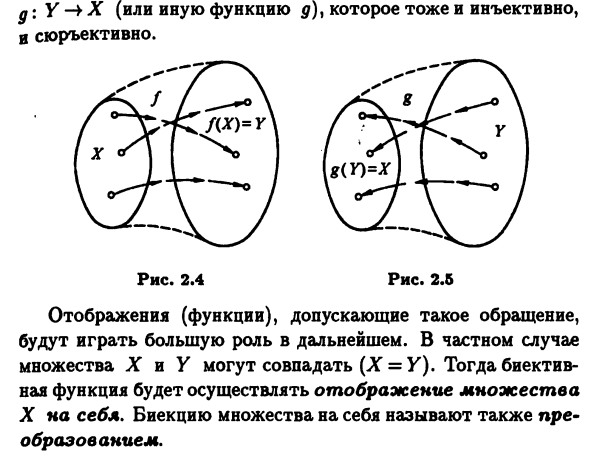
По сути, функция / в этом случае устанавливает взаимно однозначное соответствие между множествами X и У, и потому ее часто называют взаимно однозначной функцией. Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.
При этом никакие два элемента из X не могут быть соединены стрелкой с одним и тем же элементом из У, ибо / инъективна, и никакие два элемента из У не могут быть соединены стрелками с одним и тем же элементом из X из-за требования единственности образа в определении 2.1 отображения.
Каждый элемент из X участвует в попарном соединении, поскольку X — область определения функции /. Наконец, каждый элемент из У тоже участвует в одной из пар, ибо / сюръективна. Роли X и У в этом случае как бы совершенно одинаковы, и если повернуть все стрелки вспять (рис. 2.5), то получим иное отображение или иную функцию д), которое тоже и инъективно, в сюръективно. Отображения (функции), допускающие такое обращение, будут играть большую роль в дальнейшем.
| В частном случае множества X и У могут совпадать (X = У). |
Тогда биективная функция будет осуществлять отображение множества X на себл. Биекцию множества на себя называют также пре-образов анием. 2.3. Обратное отображение Пусть /: X —? У — некоторая биекция и пусть у € У. Обозначим через /_1(у) единственный элемент х€Х, такой, что /(г) = у. Тем самым мы определим некоторое отображение 9 : Y Xу которое является снова биекцией. Ее называют обратным отображением, или обратной биекцией к /. Часто ее также называют просто обратной функцией и обозначают /»*. На рис. 2.5 функция д как раз и является обратной к /, т.е. д = f’1.
Возможно вам будут полезны данные страницы:
Очевидно, что каждой паре (а, Ь) действительных чисел а, 6 6R соответствует на плоскости точка М, имеющая эти числа своими координатами. И обратно, каждой точке М плоскости соответствует пара (а, 6) действительных чисел а и 6. В общем случае пары (а, Ь) и (6, а) определяют разные точки, т.е. существенно, какое из двух чисел а и b стоит в обозначении пары на первом месте. Таким образом, речь идет об упорядоченной паре. В связи с этим пары (а, 6) и (6, а) считают равными между собой, и они определяют одну и ту же точку на плоскости, если только а = 6. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Множество всех пар действительных чисел, а также множество точек плоскости обозначают R2. Это обозначение связано с важным в теории множеств понятием прямого (или дек ар-това) произведения множеств (часто говорят просто о произведении множеств). Определение 2.2.
Произведением множеств А и В называют множество Ах В возможных упорядоченных пар (ж, у), где первый элемент взят из А, а второй — из В, так что Равенство двух пар (х, у) и (&’, у’) определяют условиями х = х’ и у = у7. Пары (я, у) и (у, х) считают различными, если хфу. Это особенно важно иметь в виду, когда множества А и В совпадают. Поэтому в общем случае А х В ф В х Л, т.е. произведение произвольных множеств не коммутативно, но оно дистрибутивно по отношению к объединению, пересечению и разности множеств: где обозначает одну из трех названных операций.
Произведение множеств
Если же X С R, а У = R2, то график функции также есть множество точек в R3, которое может представлять некоторую линию, пересекаемую плоскостью х = const лишь в одной точке М с тремя координатами х> yi, у2 (рис. 2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
MT1102: Линейная алгебра (введение в математику)
Пусть %%f%% — отображение множества %%X%% в множество %%Y%%.
Инъективное отображение
Отображение %%f%% называется инъективным,
Другими словами, отображение %%f%% инъективно, если образы различных элементов из %%X%% также различны.
Пример
Сюръективное отображение
Другими словами, отображение %%f%% сюръективно, если каждый элемент %%y \in Y%% является образом хотя бы одного элемента %%x \in X%%.
Пример
Отображение %%f(x) = \sin(x)%%, определенное на множестве %%\mathbb R%%, с множеством %%Y = [-2,2]%% не является сюръективным, т.к. для элемента %%y = 2 \in Y%% нельзя найти прообраз %%x \in X%%.
Биективное отображение
Отображение %%f%% называется биективным, если оно инъективно и сюръективно. Биективное отображение также называется взаимно однозначным или преобразованием.
Обычно, словосочетания «инъективное отображение», «сюрьективное отображение» и «биективно отображение» заменяют на «инъекция», «сюръекция» и «биекция» соответственно.
Обратное отображение
Пусть %%f: X \to Y%% — некоторая биекция и пусть %%y \in Y%%. Обозначим через %%f^<-1>(y)%% единственный элемент %%x \in X%% такой, что %%f(x) = y%%. Тем самым мы определим некоторое новое отображение %%g: Y \to X%%, которое снова является биекцией. Ее называют обратным отображением.
Пример
Пусть %%X, Y = \mathbb R%% — множество действительных чисел. Функция %%f%% задана формулой %%y = 3x + 3%%. Имеет ли данная функция обратную? Если да, то какую?
Для того чтобы узнать имеет ли данная функция обратную ей, необходимо проверить является ли она биекцией. Для этого проверим является ли данное отображение инъективным и сюръективным.
Так как %%f%% — инъекция и сюръекция, то %%f%% — биекция. И, соответственно, обратным отображением является %%x = \frac
Элементы абстрактной алгебры. Часть II. Виды отображений.
И снова привет. Сегодня мы поговорим о видах отображений. Надеюсь, пост https://pikabu.ru/story/yelementyi_abstraktnoy_algebryi_chas. был усвоен.
P. S. Не стоит ограничивать отображения числовыми функциями: им от этого обидно. Например, соответствие между множеством всех когда-либо живших людей и множеством родителей (тут упорядоченные пары) будет отображением.
Общий взгляд на отображение
Определение. Отображение f множества A на множество B называется сюръективным, если для каждого элемента из B найдётся хотя бы один прообраз в A.
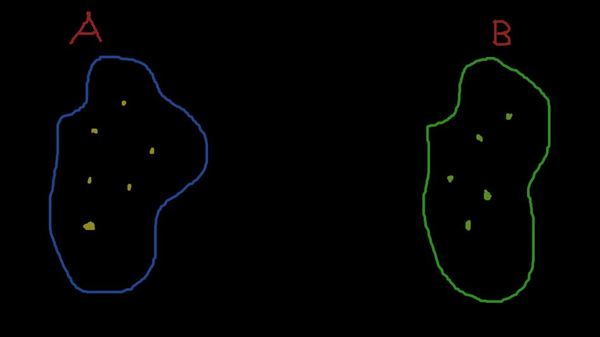
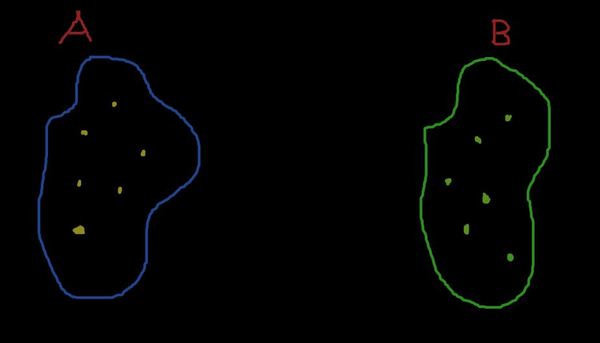
Чёйта такое? Это легко пояснить на схемах со стрелочками. Итак, нарисуем множества A и B
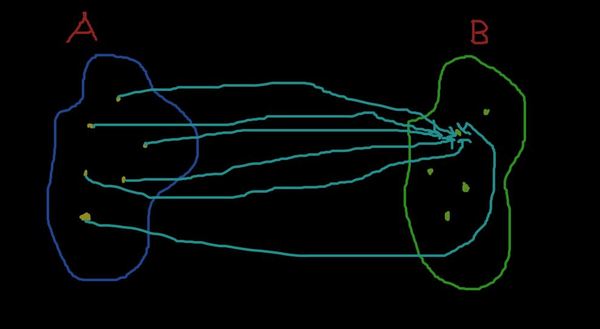
Зададим отображение множества A на B. Оно будет ставить каждой точечке из A какие-то точечки из B. Как всё это может выглядеть? Ну, например, так
Все точки из A превратились в конкретную точку из B. Кстати, такое отображение называется постоянным.
А может быть и так
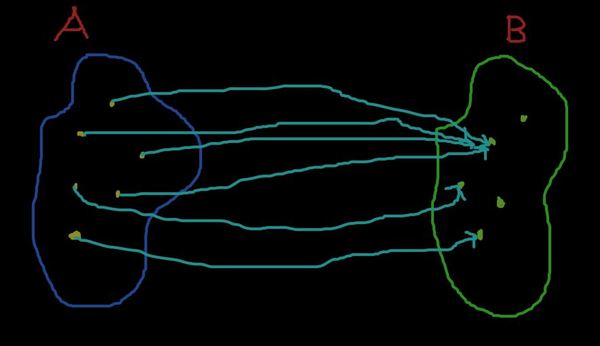
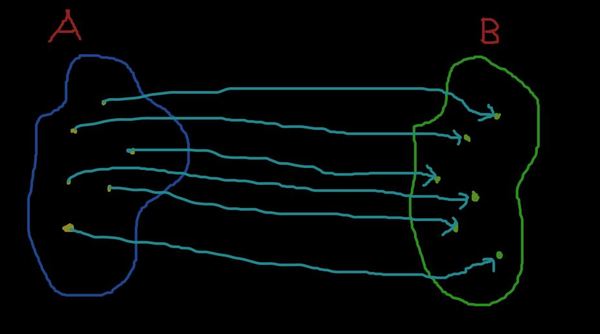
Давайте исправим ситуацию и наделим все точки прообразами в A.
Шедевр. Теперь каждый элемент в B имеет прообраз в A! И, конечно, это свойство нашего отображения (именно оно диктует, кто и какой будет иметь прообраз). А теперь посмотрите определение сюръекции и заметьте, что наше некое отображение суть пример сюръекции!
Нижняя точка выделяется тем, что имеет два прообраза в A (в неё входят две стрелочки). Это тоже особенность отображения. С тем же успехом мы можем взять одну стрелочку из нижней точки и перетащить её в верхнюю. Тогда, разумеется, получится новая сюръекция.
Давайте добавим ещё примеров.
Числовая функция f(x) = x, отображающая R на R, суть сюръекция.
Отображение g множества трёхзначных чисел на множество цифр от 0 до 9, ставящее в соответствие трёхзначному числу его 2-е число (в середине которое), суть сюръекция. Действительно, для каждого числа от 0 до 9 найдётся некоторое трёхзначное число. Например, для 1 можно найти 119, 118, 610 и так далее.
Но найти сюръективное отображение одного множества на другое не всегда возможно. Давайте отныне договоримся (это не касается примеров), что мы будем рассматривать конечные множества.
Итак, между двумя множествами A и B можно установить сюръективное отображение тогда и только тогда, когда n(A) >= n(B).
И вправду. Если n(A) n(B), мы не сможем напихать стрелочки так, чтобы элементы в B имели только один прообраз в A (не обязательно все элементы = это не обязательно сюръекция). У нас просто в A будет избыток стрелочек!
Давайте посмотрим на случай n(A) = n(B).
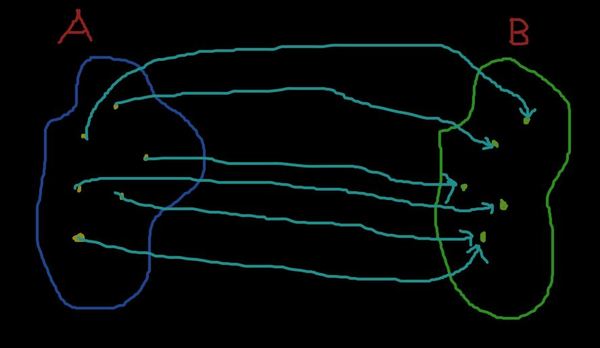
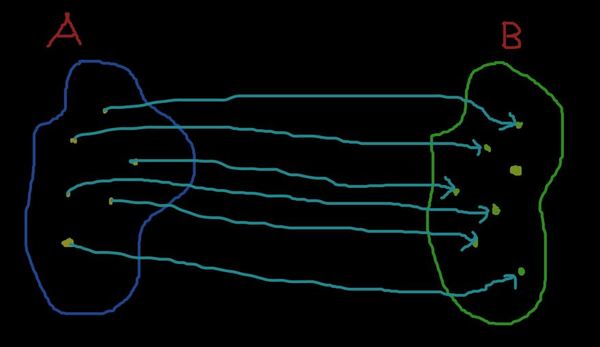
Среди всех возможных отображений выделяется один класс отображений, который выглядит так
Красиво! Элементы в B имеют ровно один прообраз в A. Никаких избытков стрелочек, все равноправны, всё по Марксу-Энгельсу.
Короче говоря, разные элементы A переходят в разные элементы B (имеют разные образы при отображении).
Определение. Отображение, при котором разные элементы отображаемого множества имеют разные образы, называется инъекцией.
Наука | Научпоп
6.1K поста 69K подписчиков
Правила сообщества
ВНИМАНИЕ! В связи с новой волной пандемии и шумом вокруг вакцинации агрессивные антивакцинаторы банятся без предупреждения, а их особенно мракобесные комментарии — скрываются.
Основные условия публикации
— Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
— Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
— Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
— Видеоматериалы должны иметь описание.
— Названия должны отражать суть исследования.
— Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
Не принимаются к публикации
— Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
— Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
— Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
— Оскорбления, выраженные лично пользователю или категории пользователей.
— Попытки использовать сообщество для рекламы.
— Многократные попытки публикации материалов, не удовлетворяющих правилам.
— Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает @SupportComunity и общество пикабу.
>делятся на сюръекцию, инъекцию, биекцию и всё остальное
Не совсем хорошо сказано.
Биекция является сюръекцией и инъекцией, слово «делятся» обычно подразумевает разделение на неперсекающиеся классы.
Помню эту херь в универе, так и не разобрался НАХРЕНА ЭТО ВООБЩЕ НУЖНО? Почему когда объясняют подобную поеботу, не дают сразу какой нибудь жизненный пример, где это используется, чтоб можно было сразу понять, но нет, вот тебе куча какой то сумбурной херни, зубри это
Теперь серьезно, я так и не понял, почему для сюръективного отображения мощность множества прообразов должна быть выше мощности множества образов. В определении сюръекции вроде нигде не говорится, что каждый элемент из А может иметь лишь один образ.
Сюръективное не инъективное отображение: f: R²→R, f(x,y)=x ∀(x,y).
Не сюръективное инъективное отображение: f: R→R², f(x)=(x,0) ∀x.
Сюръективное инъективное отображение: f: R²→R², f(x,y)=(x+y,x-y) ∀(x,y).
Ох я помню изучал такую фигню на физмате, а потом отчислился и поступил в медунивер.
Какой приз за правильные ответы?
Элементы абстрактной алгебры. Часть I. Введение. Отображения (общие понятия).
Здравствуй, дорогой читатель!
В первую очередь этот цикл рассказов обращён ко всем тем, кто не варится в котле математики, но интересуется последним. Это школьники, прозревшие студенты гуманитарных специальностей и просто все любители абстрактных вещей.
• Какие-никакие азы школьной математики, которые знает каждый хорошист.
Во-вторых, я буду давать по ходу изложения упражнения. Советую их все выполнять. Если возникнут проблемы, то пишите в комментарии.
Вот. Первой на очереди будет теория групп. Поехали, кубик Рубика ждёт!
Отображения (общие понятия)
Всегда нужно с чего-то начинать, с какого-то общего языка для конкретно данной области. Например, мат. анализ начинают с действительных чисел и функций действительного переменного, топологию с теории множеств. Нам же нужны множества и отображения. Первое мы опустим, потому что мы лишь знакомимся. Оно будет поясняться по ходу дела, косвенно. А вот отображения мы с вами просто обязаны рассмотреть в силу причин, которые будут известны чуть позже. Итак.
Помните те функции, которые проходят на уроке алгебры? Давайте посмотрим на них внимательнее.
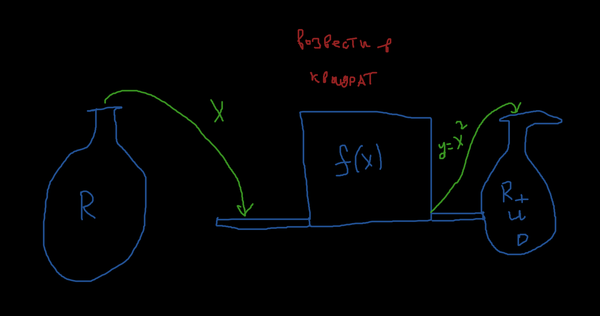
У нас есть мешок всех действительных чисел (область определения функции), некая машина, которая имеет вход и выход, и мешок, в который помещаются преобразованные в машине элементы. Мы достаём из мешка некоторое число x, несём его на машину, которая исполняет заданный функцией алгоритм («возведи в квадрат»), а после выдаёт уже преобразованный элемент y и скидывает его в мешок. Вот так и работает функция.
Если мы каким-то боком перетащим всё содержимое из мешка R в машину, то получим мешок действительных положительных цифр и нуля.
Давайте перетащим первую цифру. Что берём? Давайте, пожалуй, 2.
Итак, берём двойку и несём её на вход машины. Она, эта f(), принимает в себя 2, получая f(2). Далее она выполняет алгоритм и выдаёт нам 4, складывая его в мешок. Видите, как всё просто?
Упражнение 1. Попрактикуйтесь с цифрами 5, 70, 1000.
Однако мы можем задать с такую вещь:
Определение. Две функции f(x) и g(x) равны тогда и только тогда, когда совпадают их области определения и каждый элемент из области определения они преобразуют одинаково.
Пусть наши функции заданы на одной и той же области определения, пусть они преобразуют все элементы из неё одинаково, кроме одного. Но если этот один «таракан» существует, то он рушит всё равенство! Аналогично с областями определения.
Упражнение 2. Какие из следующих функций равны:
Обратите внимание на выделенное слово. Мы должны задавать первый мешок так, чтобы каждый элемент можно было бы запихать в машину. Это не всегда возможно.
Пусть машина имеет правило 1/x. Если наш мешок суть R, то там валяется 0. Можем ли мы затолкать в машину ноль? Нет, она будет упорно его выплёвывать, может, даже сломается, ведь ей, бедной, придётся выдавать на выходе 1/0. Ох, жалко машину. Пожалейте машину и выбросьте из мешка те элементы, которые не заталкиваются в машину.
Познакомимся с несколько новой символикой.
Вот у нас функция f(x). Вытащим оттуда букву f. Она символизирует правило, диктующее соответствие. Тогда вот так
и обозначается отображение множества A во множество B по правилу f.
Если брать нашего робота, то эта запись показывает преобразования мешков. Мы вместо отдельных элементов первого мешка заталкиваем в машину весь мешок. На выходе получаем новый мешок, содержащий элементы, преобразованные по правилу f. В первом примере у нас мешок R преобразуется в (R+) + 0.
Если брать x = 2, то получится:
Терминология вполне естественна, не правда ли?
Упражнение 3. Исследуйте какие-нибудь известные вам функции в новых терминах и символах.
На сегодня всё. Продолжим чуть позже. На следующем «уроке» мы посмотрим на разные виды отображений и найдём связь с комбинаторикой. Всего доброго.
только для инъекций
Инъективная функция не обязательно должна быть сюръективной (не все элементы кодомена могут быть связаны с аргументами), а сюръективная функция не обязательно должна быть инъективной (некоторые изображения могут быть связаны с более чем одним аргументом). Четыре возможных комбинации инъективных и сюръективных признаков показаны на соседних диаграммах.
СОДЕРЖАНИЕ
Инъекция
Ниже приведены некоторые факты, связанные с инъекциями:
Surjection
Ниже приведены некоторые факты, относящиеся к сюрпризам:
Биекция
Ниже приведены некоторые факты, относящиеся к предубеждениям:
Мощность
Примеры
Важно указать домен и кодомен каждой функции, поскольку при их изменении функции, которые кажутся одинаковыми, могут иметь разные свойства.
Характеристики
Теория категорий
История
Инъективно-сюръективно-биективная терминология (как существительные, так и прилагательные) была первоначально введена французской группой Бурбаки до их широкого распространения.
Сюръекция, инъекция и биекция



Сюръекция, инъекция и биекция
Установить согласно в соответствии с определением 2.1. F: X- ¥ Y сбрасывается для Vy € YЗх € X: > (X) = у. На рисунке в данном случае каждый элемент По крайней мере, одна стрелка ведет к множеству У (рисунок 2.2). В то же время Некоторые элементы Y могут иметь несколько стрелок. Эта функция не обязательно сюръективна. Стрелка Не все элементы множества Y связаны (рисунок 2.3). так Функция f: X-> Y, если есть два Различные элементы из X имеют свои изображения Отображение / два разных элемента Ue Y, или Vy € f (X) СY 3 \ xeX: f (x) = y. Отображение F: X- * Y Называется биекция
Стригущий лишай на все элементы Стрелка, то / называется функцией впрыска, или Инъекции. Людмила Фирмаль
Проецирование каждого элемента GY это изображение Некоторые только призы Элемент X, т.е. Vy 6 f (X) = Y 3 \ x € X: f (x) = y. по существу Функция / в этом случае Установите 1: 1 Соответствие между множеством X И U, поэтому его часто называют Индивидуальная функция. Очевидно, что функция / биективна. Когда она и выстрел, и выстрел. здесь Корпус стрелки (рисунок 2.4) соединяет элементы попарно От X с каждым элементом из U. Кроме того, 2 Элементы из X не могут быть связаны одной стрелкой С тем же элементом из Y, / инъективен, нет двух Y элементы не могут быть связаны одной стрелкой И Х с тем же элементом, требование уникальности Карта Определение 2.1 изображение.
Каждый элемент или X Поскольку X является регионом, он будет участвовать в спаривании Определение функции. Наконец, каждый элемент Y Поскольку / является выстрелом, он присоединяется к одной из пар. Роль X и U В этом случае, это точно так же, как это, Все стрелки перевернуты (рисунок 2.5), что дает другое отображение Рисунок 2.3 d: Y- * X (или другая функция ξ). Это тоже выстрел. И умозрительно. Рисунок 2.4 Рисунок 2.5 Отображения (функции), которые позволяют такие вызовы, Это сыграет большую роль в будущем. Особые случаи Наборы X и Y могут совпадать (X = Y). тогда Функция bijection отображает набор Мой икс Биекция набора к себе предварительно Образование.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института