Как доказать что отрезок является высотой
Определение и свойства высоты треугольника
В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.
Определение высоты треугольника
Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.
Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).
Обычно высота обозначается буквой h (иногда как ha – это означает, что она проведена к стороне a).
Высота в разных видах треугольников
В зависимости от вида фигуры высота может:
Свойства высоты треугольника
Свойство 1
Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).
Свойство 2
При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:
Свойство 3
Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.
Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.
Свойство 4
Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.
Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.
Свойства высоты прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.
Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть
Свойства высоты в прямоугольном треугольнике
Свойство 1
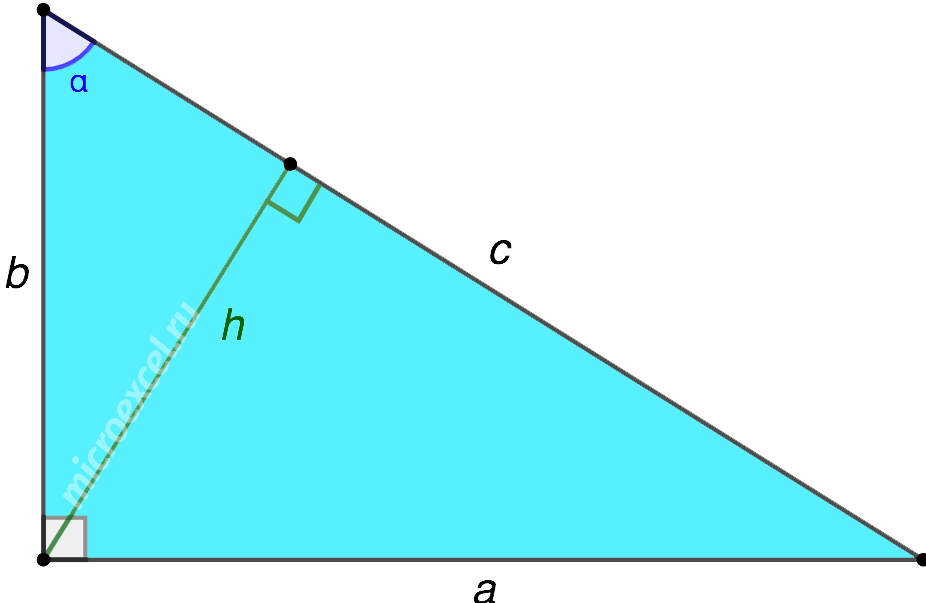
В прямоугольном треугольнике две высоты (h1 и h2) совпадают с его катетами.
Третья высота (h3) опускается на гипотенузу из прямого угла.
Свойство 2
Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.
Свойство 3
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC. Следовательно, ∠BAD = ∠ACD.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.
Свойство 4
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:
1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:
2. Через длины сторон треугольника:
Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :
Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение
Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
Доказательство
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
ВЫСОТА ТРЕУГОЛЬНИКА В ЗАДАЧАХ
Высота треугольника участвует во многих интересных задачах, о которых будет идти речь в данном материале.
Докажем, прежде всего, что высоты треугольника (или их продолжения) пересекаются в одной точке.
□ 1 способ. Проведем через вершины треугольника прямые, параллельные их противолежащим сторонам и получим треугольник (рис.1). Тогда высоты данного треугольника являются, очевидно, серединными перпендикулярами сторон треугольника, поэтому они пересекаются в одной точке Н, она называется ортоцентром данного треугольника.
3 способ. Найдем длины отрезков (где )
Рассмотрим некоторые задачи.
□ Так как – как углы со взаимно перпендикулярными сторонами
(рис.4), то Рассмотрев подобные треугольники и получим равенство (1). ■
Задача 2.
Задача3.
Треугольник вписан в окружность. Доказать, что отрезок, соединяющий основания двух высот треугольника, перпендикулярен к радиусу окружности, проведенному в третью вершину.
Задача 4.
В треугольнике стороны ортоцентрического треугольника равны 5, 12 и 13. Найти площадь данного треугольника.
□ Пусть и – высоты, и (рис.7).
Задача5.
2) Из равенства углов и следует, что прямые ипересекаются в одной точке – центре описанной окружности треугольника.
Шарыгин И. Ф. Геометрия. Задачник 9-11М., Дрофа, 1997
Свойства высот треугольника. Ортоцентр
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если 

Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам
Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)
2. В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и