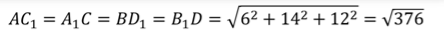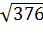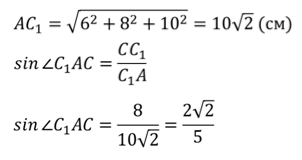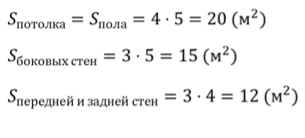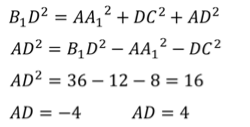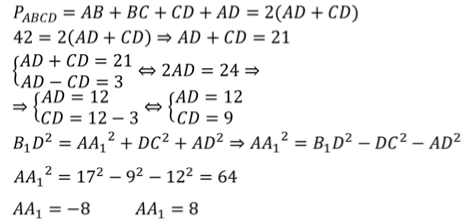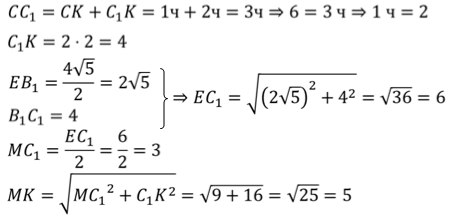Как доказать что параллелепипед прямоугольный

Прямоугольный параллелепипед. Что это такое?

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

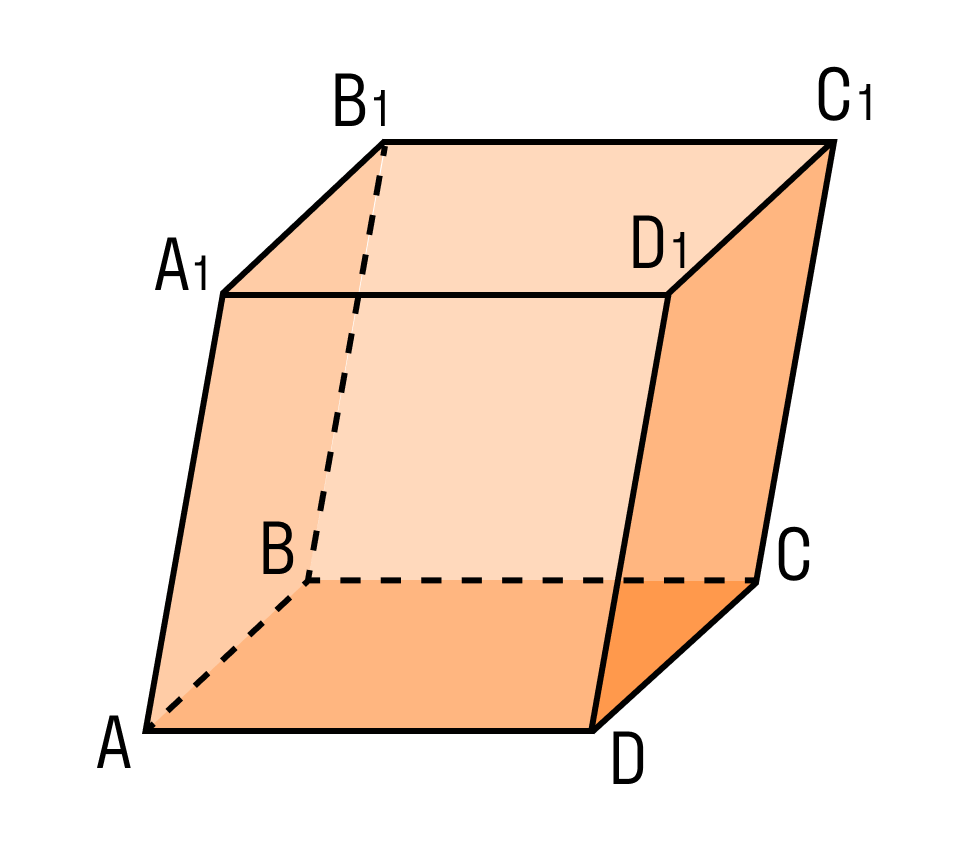
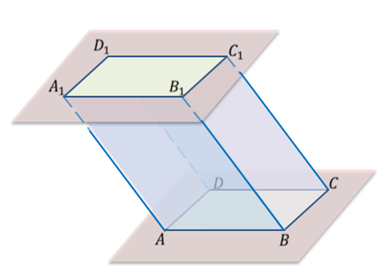
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

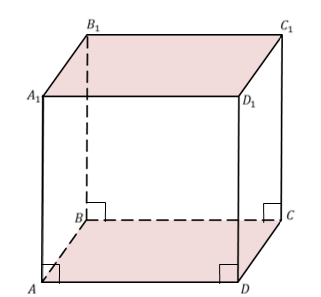
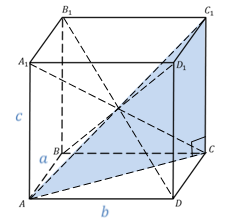
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

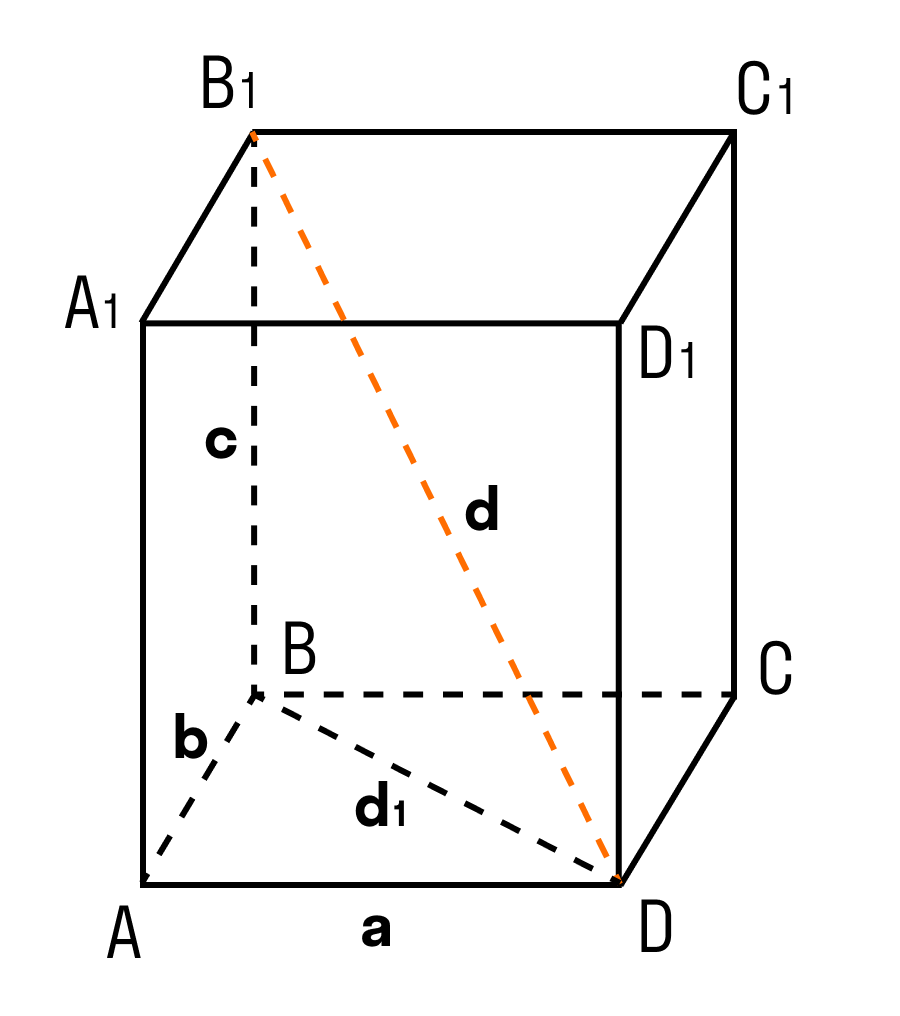
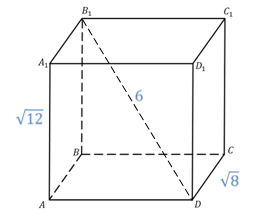
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

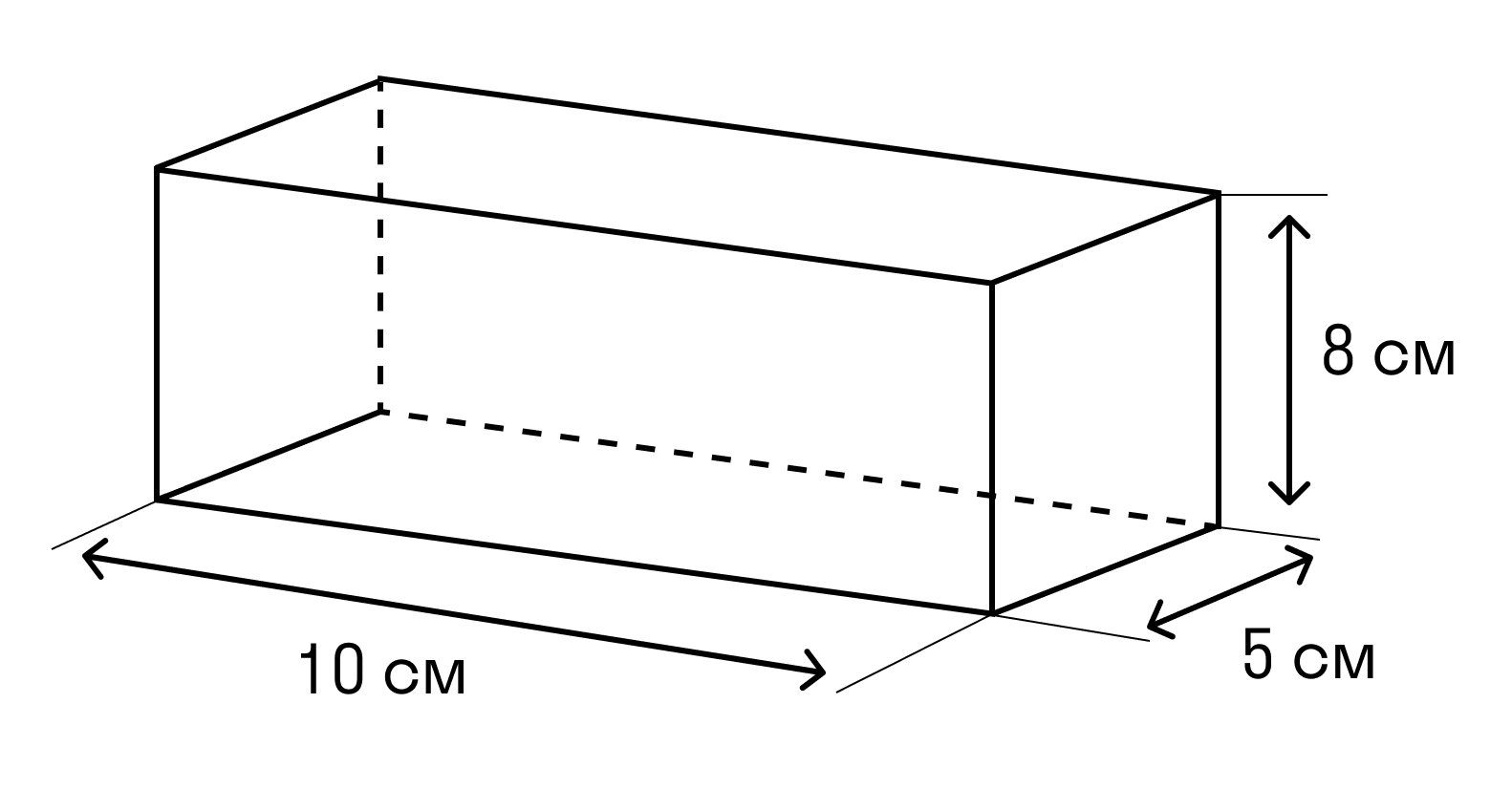
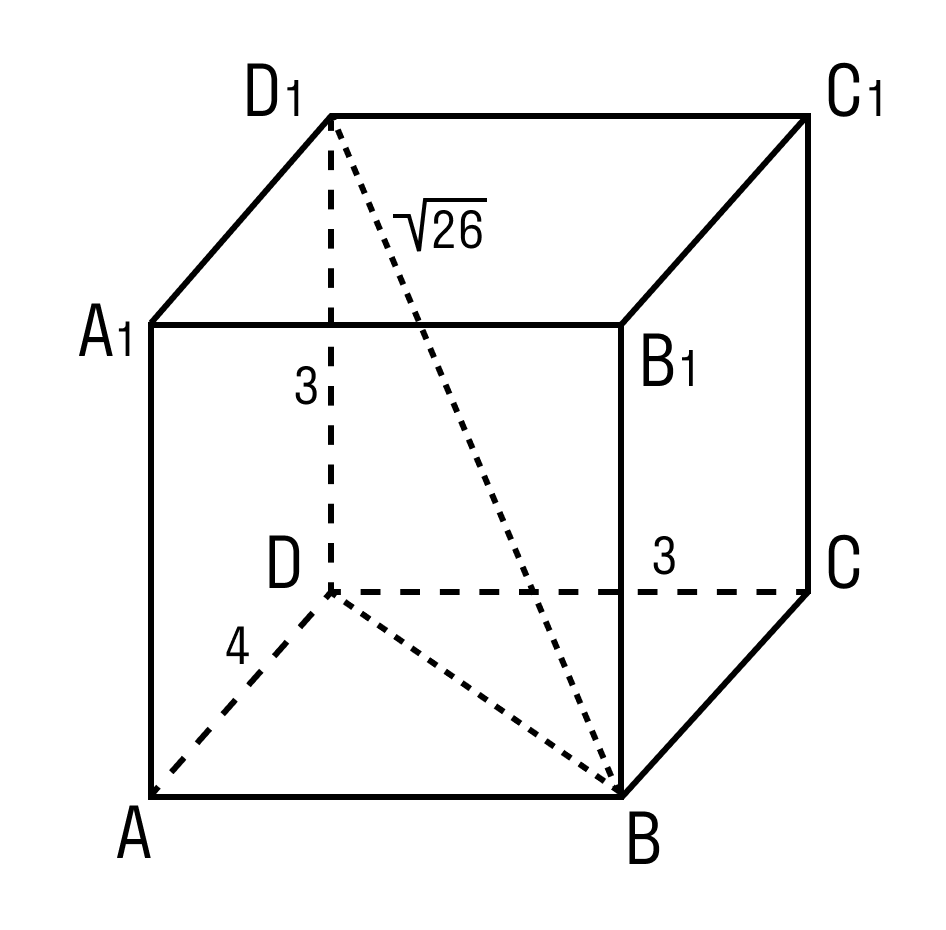
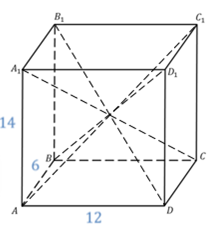
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

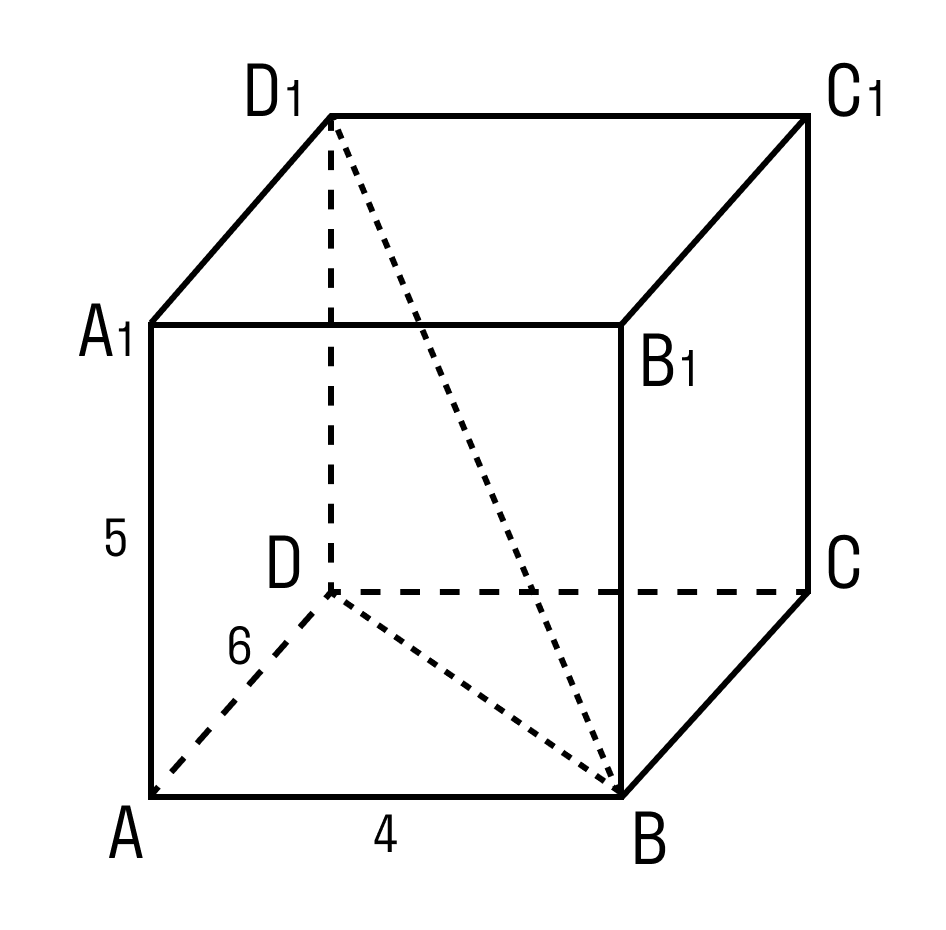
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

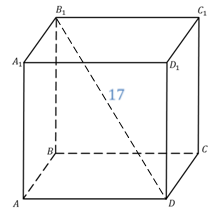
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник

Как доказать что параллелепипед прямоугольный

1. Противоположные грани параллелепипеда параллельны и равны.

(фигуры равны, то есть их можно совместить наложением)

АВСD = А 1 В 1 С 1 D 1 (равные параллелограммы по определению),

АА 1 В 1 В = DD 1 С 1 С (так как АА 1 В 1 В и DD 1 С 1 С – противоположные грани параллелепипеда),

АА 1 D 1 D = ВВ 1 С 1 С (так как АА 1 D 1 D и ВВ 1 С 1 С – противоположные грани параллелепипеда).

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

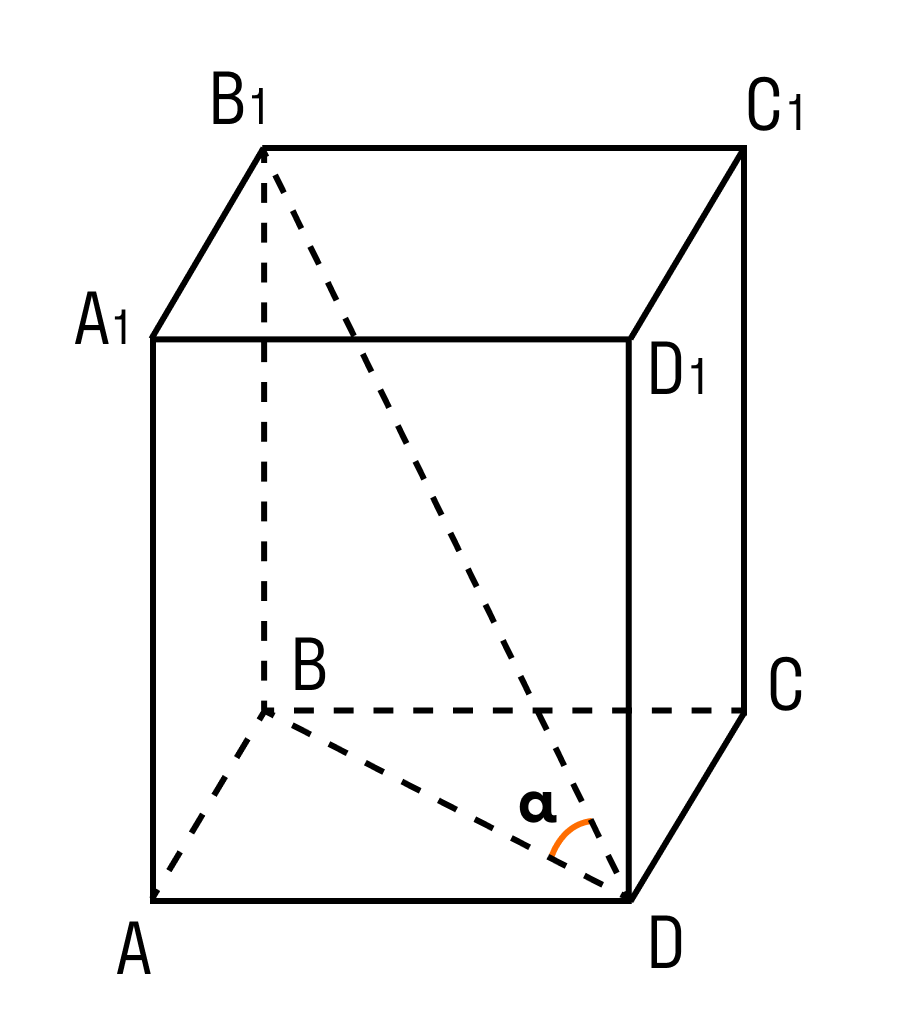
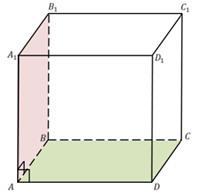
Пусть боковое ребро АА 1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА 1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.

Параллелепипед АВСDА 1 В 1 С 1 D 1 – прямоугольный (рис. 4), если:

1. АА 1 ⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).

2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.

1. В прямоугольном параллелепипеде все шесть граней прямоугольники.

АВСD и А 1 В 1 С 1 D 1 – прямоугольники по определению.

2. Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольники.

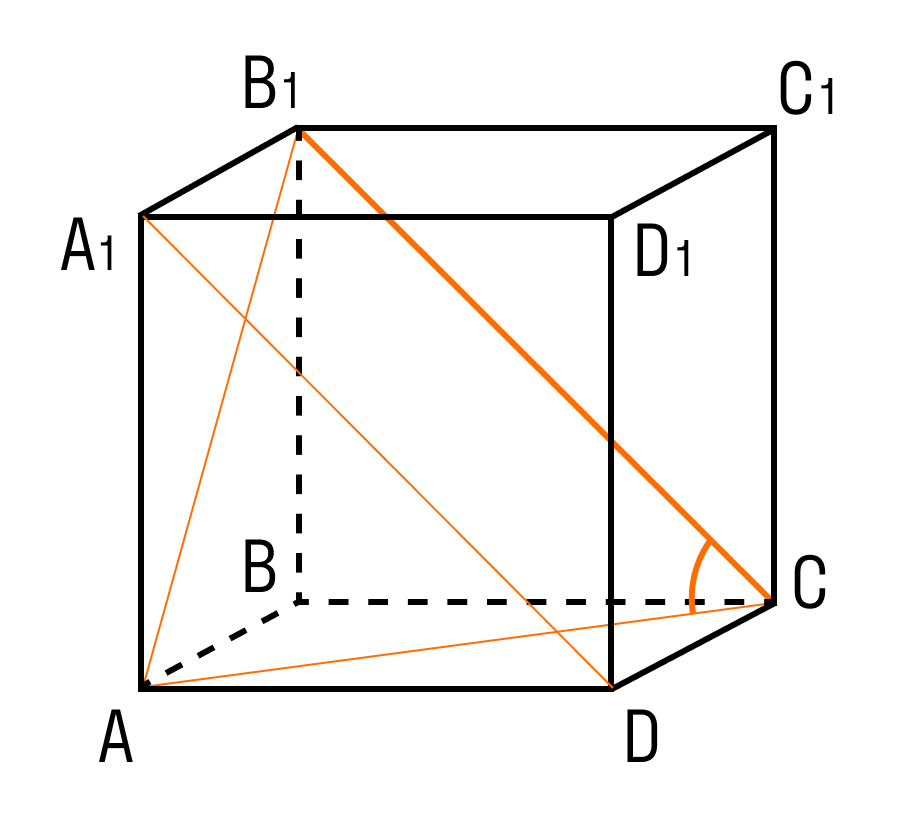
3. Все двугранные углы прямоугольного параллелепипеда прямые.

Рассмотрим, например, двугранный угол с ребром АВ, т. е. двугранный угол между плоскостями АВВ 1 и АВС.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.

Примечание. Длины трех ребер, исходящих из одной вершины, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.

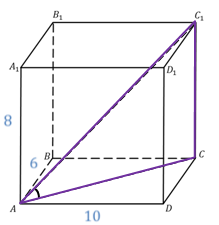
Дано: АВСDА 1 В 1 С 1 D 1 – прямоугольный параллелепипед (рис. 5).

Доказать: .

Прямая СС 1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС 1 А – прямоугольный. По теореме Пифагора:

Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:

Но ВС и AD – противоположные стороны прямоугольника. Значит, ВС = AD. Тогда:

Следствие : Диагонали прямоугольного параллелепипеда равны.

Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 6), тогда АС 1 = СА 1 = В 1 D = DВ 1 =

Источник

Прямоугольный параллелепипед

Урок 24. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямоугольный параллелепипед»

Прежде чем приступить к изучению нового материала, давайте вспомним, какую фигуру мы назвали параллелепипедом, основные свойства параллелепипеда.

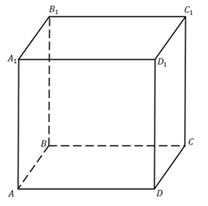
Напомним, что параллелепипедом мы назвали поверхность, составленную из двух равных параллелограммов ABCD и A₁B₁C₁D₁ и четырех параллелограммов ABB₁A₁, BCC1B₁, CDD₁C₁, DAA₁D₁.

Повторим свойства параллелепипеда. Противоположные грани параллелепипеда параллельны и равны. Например, в параллелепипеде, который показан на рисунке грань ABCD равна и параллельна грани A₁B₁C₁D₁, грань AA₁B₁B равна и параллельна грани DD₁C₁D, грань AA₁D₁D равна и параллельна грани BB₁C₁C.

Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Эти свойства мы уже доказывали.

Когда мы изучали тему «Параллелепипед», мы говорили, что, если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым. Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.

Сегодня на уроке мы познакомимся с прямоугольным параллелепипедом поближе.

Форму прямоугольного параллелепипеда имеют многие предметы.

Давайте посмотрим на рисунок.

Основаниями этого прямоугольного параллелепипеда служат прямоугольники ABCD и A₁B₁C₁D₁, боковые рёбра AA₁, BB₁, CC₁, DD₁ перпендикулярны к основаниям. То есть можно записать, что AA₁ перпендикулярно AB, то есть боковая грань AA₁B₁B – прямоугольник. Аналогично, можно показать, что все боковые грани прямоугольного параллелепипеда являются прямоугольниками. Таким образом, мы обосновали свойство прямоугольного параллелепипеда.

Сформулируем его. В прямоугольном параллелепипеде все шесть граней – прямоугольники.

Полуплоскости, в которых расположены смежные грани параллелепипеда, образуют двугранные углы, которые называются двугранными углами параллелепипеда.

Рассмотрим, например, двугранный угол с ребром AB, то есть двугранный угол между плоскостями ABB₁ и ABC.

По другому этот угол можно записать так: угол A₁ABD.

Возьмем на ребре AB, например, точку А. AA₁ – перпендикуляр к ребру AB в плоскости ABB₁, АD– перпендикуляр к ребру АB в плоскости ABC. Значит, угол A₁AD – линейный угол двугранного угла. Это прямой угол, значит, двугранный угол при ребре AB – прямой.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые. Это утверждение является еще одним свойством прямоугольного параллелепипеда.

Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда. Например, у параллелепипеда, который изображен на рисунке в качестве измерений можно взять длины ребер AB, АD и AA₁.

Понятно, что если мы говорим, например, о размерах коробки, которая имеет форму прямоугольного параллелепипеда, то мы вместо слова измерения используем слова: длина, ширина и высота.

Давайте вспомним, что в прямоугольнике квадрат диагонали равен сумме квадратов смежных сторон. Длины смежных сторон можно назвать измерениями прямоугольника. Тогда это утверждение можно переформулировать так: квадрат диагонали прямоугольника равен сумме квадратов двух его измерений.

Аналогичным свойством обладает и прямоугольный параллелепипед.

Сформулируем теорему. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Пусть дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Тогда нам надо доказать, что, например, .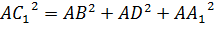

Поскольку параллелепипед прямоугольный, то ребро CC₁ перпендикулярно к основанию ABCD. А, значит, угол ACC₁ – прямой.

Рассмотрим треугольник ACC₁. Это прямоугольный треугольник, значит, по теореме Пифагора можно записать, что .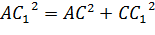

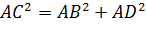
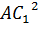
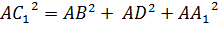
AC – диагональ прямоугольника ABCD. Значит, по свойству диагоналей прямоугольника можно записать, что . Кроме того, мы знаем, что ребро CC₁ равно AA₁. Тогда подставив все в выражение для , получим, что .

Что и требовалось доказать.

Теперь давайте сформулируем и докажем следствие из этой теоремы.

Диагонали прямоугольного параллелепипеда равны.

Это следствие легко доказать, если мы посмотрим на доказательство теоремы. Мы могли взять вместо диагонали AC₁, например, диагональ CA₁ или диагонали BD₁ или DB₁, но мы бы получили то же самое выражение.

Если мы обозначим измерения прямоугольного параллелепипеда буквами a, b, c, тогда можно записать, что .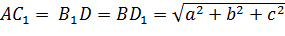

Если все измерения прямоугольного параллелепипеда равны, то такой прямоугольный параллелепипед называется кубом.

Поскольку все измерения куба равны, значит, все грани куба – квадраты.

Решим несколько задач.

Задача. Измерения прямоугольного параллелепипеда равны 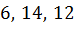. Найти длины диагоналей прямоугольного параллелепипеда.

Воспользуемся следствием из теоремы и запишем, что все диагонали прямоугольного параллелепипеда равны.

Теперь применим теорему и запишем, что диагонали равны корню квадратному из суммы квадратов измерений прямоугольного параллелепипеда.

Поскольку мы знаем, что все диагонали параллелепипеда равны, при решении задач мы будем изображать только одну диагональ параллелепипеда, если условие задачи не потребует изобразить больше диагоналей.

Ответ.

Решим еще одну задачу.

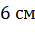
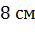
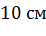
Задача. В прямоугольном параллелепипеде измерения равны , , . Найти диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания.

Ответ. ; .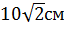

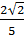
А теперь давайте решим одну задачу, которую очень часто решают люди, которые делают ремонт.

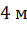
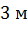
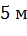
Задача. Измерения комнаты равны , , . Подсчитать площадь пола, потолка, и стен комнаты.

Каждая из граней прямоугольного параллелепипеда – прямоугольник. Для того, чтобы найти площадь каждой грани, достаточно перемножить соответствующие измерения каждого прямоугольника.

Ответ. 20м 2 ; 15 м 2 ; 12 м 2

Решим еще одну задачу.

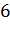
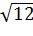
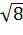
Задача. Диагональ прямоугольного параллелепипеда равна , а два измерения равны соответственно и . Найти третье измерение прямоугольного параллелепипеда.

Запишем формулу, связывающую квадрат диагонали прямоугольного параллелепипеда и квадраты измерений прямоугольного параллелепипеда.

(Очевидно, что измерение прямоугольного параллелепипеда не может быть отрицательным числом).

Решим еще одну задачу.

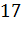
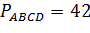
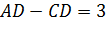
Задача. Диагональ прямоугольного параллелепипеда равна , , . Найти третье измерение прямоугольного параллелепипеда.

Решим еще одну задачу.

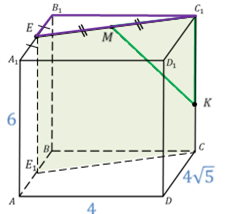
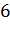
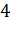
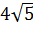
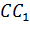
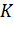
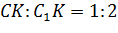
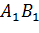
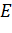
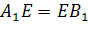
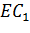
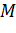
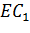
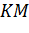
Задача. Измерения параллелепипеда равны , , . На ребре прямоугольного параллелепипеда, изображенного на рисунке, дана точка такая, что отношение . На ребре отмечена точка так, что . На отрезке отмечена точка , которая является серединой отрезка . Найти длину отрезка .

Сначала построим плоскость, в которой будет лежать отрезок МК. Для этого достаточно из точки Е опустить перпендикуляр на грань ABCD. Получим точку E₁. Тогда в плоскости EE₁C и будет лежать искомый отрезок КМ.

Найдем длину отрезка KC₁.Рассмотрим треугольник EB₁C₁.

Теперь из треугольника MKC₁ определим МК.

Подведем итоги урока.

Сегодня на уроке мы повторили определение параллелепипеда, повторили основные свойства параллелепипеда. Дали определение прямоугольному параллелепипеду, измерениям прямоугольного параллелепипеда, рассмотрели свойства прямоугольного параллелепипеда. Решили несколько задач.

Источник