Как доказать что пирамида правильная

Пирамида

Определение

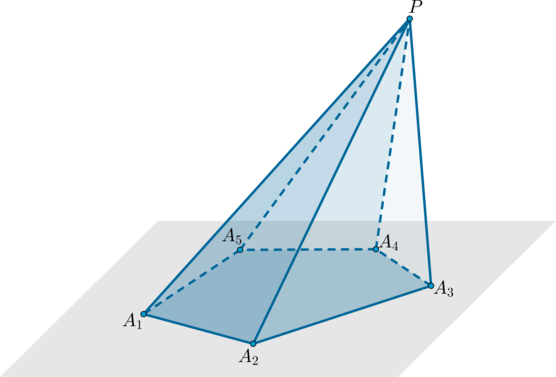
Треугольники \(PA_1A_2, \ PA_2A_3\) и т.д. называются боковыми гранями пирамиды, отрезки \(PA_1, PA_2\) и т.д. – боковыми ребрами, многоугольник \(A_1A_2A_3A_4A_5\) – основанием, точка \(P\) – вершиной.

Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Пирамида, в основании которой лежит треугольник, называется тетраэдром.

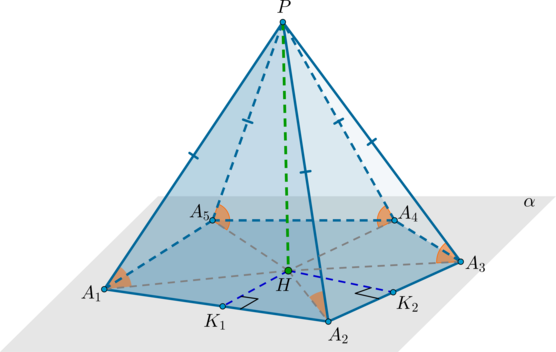
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:

\((a)\) боковые ребра пирамиды равны;

\((b)\) высота пирамиды проходит через центр описанной около основания окружности;

\((c)\) боковые ребра наклонены к плоскости основания под одинаковым углом.

\((d)\) боковые грани наклонены к плоскости основания под одинаковым углом.

Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.

Теорема

Условия \((a), (b), (c), (d)\) эквивалентны.

Доказательство

Следствие

Боковые грани правильной пирамиды – равные равнобедренные треугольники.

Определение

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.

Важные замечания

1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).

2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).

3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).

4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.

Определение

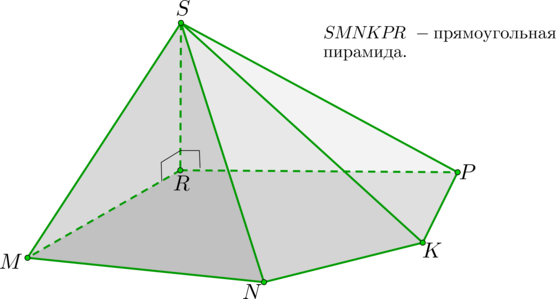
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.

Важные замечания

1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть \(SR\) – высота.

2. Т.к. \(SR\) перпендикулярно любой прямой из основания, то \(\triangle SRM, \triangle SRP\) – прямоугольные треугольники.

3. Треугольники \(\triangle SRN, \triangle SRK\) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.

Теорема

Объем пирамиды равен трети произведения площади основания на высоту пирамиды: \[V_<\text<пирамиды>>=\dfrac13 S_<\text<осн>>\cdot h\]

Следствия

Пусть \(a\) – сторона основания, \(h\) – высота пирамиды.

Теорема

Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.

Определение

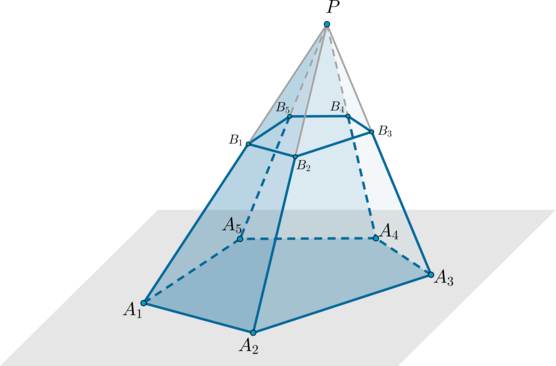
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.

Важные замечания

1. Все боковые грани усеченной пирамиды – трапеции.

2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.

Источник

Объем пирамиды (ЕГЭ 2022)

В этой статье вы поймете что такое пирамида и какими они бывают.

Вы научитесь вычислять объем пирамиды, высоту и другие ее параметры.

Вы научитесь решать задачу на доказательство (ЕГЭ №14) и записывать доказательства так, чтобы не сняли баллы на ЕГЭ.

Объем пирамиды — коротко о главном

Определение пирамиды:

Пирамида – это многогранник, который состоит из любого плоского многоугольника (основание пирамиды), точки, не лежащей в плоскости основания, (вершина пирамиды) и всех отрезков, соединяющих вершину пирамиды с точками основания.

Треугольники, в которые «сливаются» эти отрезки, называются боковыми гранями, а отрезки, проведённые к вершинам основания — это боковые ребра.

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Правильная пирамида — пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

Свойства правильной пирамиды:

Объем пирамиды:

Что такое пирамида

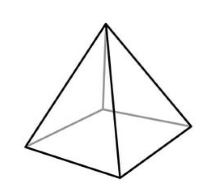
Вместо того, чтобы читать длинное определение, достаточно просто посмотреть на картинку:

Видишь: у пирамиды внизу (говорят «в основании») какой-нибудь многоугольник, и все вершины этого многоугольника соединены с некоторой точкой в пространстве (эта точка называется «вершина»).

У всей этой конструкции ещё есть боковые грани, боковые рёбра и рёбра основания.

Ещё раз нарисуем пирамиду вместе со всеми этими названиями:

Некоторые пирамиды могут выглядеть очень странно, но всё равно это – пирамиды.

Вот, например, совсем «косая» пирамида.

И ещё немного о названиях: если в основании пирамиды лежит треугольник, то пирамида называется треугольной, если четырёхугольник, то четырёхугольной, а если стоугольник, то … догадайся сам.

Высота пирамиды

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

При этом точка, куда oпустилась высота, называется основанием высоты.

Обрати внимание, что в «кривых» пирамидах высота может вообще оказаться вне пирамиды.

И ничего в этом страшного нет. Похоже на тупоугольный треугольник.

Правильная пирамида

Правильной называется такая пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

Много сложный слов?

Давай расшифруем: «В основании – правильный многоугольник» — это понятно.

А теперь вспомним, что у правильного многоугольника есть центр – точка, являющаяся центром и вписанной, и описанной окружности.

Ну вот, а слова «вершина проецируется в центр основания» означают, что основание высоты попадает как раз в центр основания. Смотри, как ровненько и симпатично выглядит правильная пирамида.

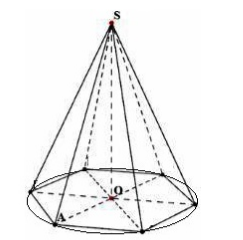
Шестиугольная правильная пирамида

В основании – правильный шестиугольник, вершина \( \displaystyle S\) проецируется в центр основания.

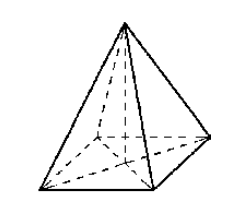
Четырехугольная правильная пирамида

В основании – квадрат, вершина \( \displaystyle S\) проецируется в точку пересечения диагоналей этого квадрата.

Треугольная правильная пирамида

В основании – правильный треугольник, вершина \( \displaystyle S\) проецируется в точку пересечения высот (они же и медианы, и биссектрисы) этого треугольника.

Очень важные свойства правильной пирамиды

В правильной пирамиде:

Объем пирамиды

Главная формула объема пирамиды

Откуда взялась именно \( \displaystyle \frac<1><3>\)?

Это не так уж просто, и на первых порах нужно просто запомнить, что у пирамиды и конуса в формуле объема есть \( \displaystyle \frac<1><3>\), а у цилиндра – нет.

Теперь давай посчитаем объем самых популярных пирамид.

Объем правильной треугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle <_<осн>>\) и \( \displaystyle H\).

\( \displaystyle <_<осн>>\) – это площадь правильного треугольника \( \displaystyle ABC\).

Вспомним, как искать эту площадь.

Используем формулу площади:

\( \displaystyle S=\frac<1><2>ab\cdot \sin \gamma \)

У нас «\( \displaystyle a\)» – это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60<>^\circ =\frac<\sqrt<3>><2>\)

Теперь найдем \( \displaystyle H\).

По теореме Пифагора для \( \displaystyle \Delta SOC\)

Чему же равно \( \displaystyle OC\)?

Это радиус описанной окружности в \( \displaystyle \Delta ABC\), потому что пирамида правильная и, значит, \( \displaystyle O\) — центр \( \displaystyle \Delta ABC\)

Найдем \( \displaystyle OC\) (Подробнее смотри в теме «Правильный треугольник»).

\( \displaystyle OC=\frac<2><3>CK\), так как \( \displaystyle O\) — точка пересечения и медиан тоже.

\( \displaystyle C<^<2>>=A<^<2>>-A<^<2>>\) (теорема Пифагора для \( \displaystyle \Delta ACK\))

Подставим \( \displaystyle OC\) в формулу для \( \displaystyle H\).

И подставим все в формулу объема:

Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:

Объем правильной четырехугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).

Здесь \( \displaystyle <_>\) и искать не нужно; ведь в основании – квадрат, и поэтому \( \displaystyle <_>=<^<2>>\).

Найдем \( \displaystyle H\). По теореме Пифагора для \( \displaystyle \Delta SOD\)

Известно ли нам \( \displaystyle OD\)? Ну, почти. Смотри:

Подставляем \( \displaystyle OD\) в формулу для \( \displaystyle H\):

А теперь и \( \displaystyle H\) и \( \displaystyle <_>\) подставляем в формулу объема.

Объем правильной шестиугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).

Как найти \( \displaystyle <_>\)? Смотри, шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете объема правильной треугольной пирамиды, здесь используем найденную формулу.

Теперь найдем \( \displaystyle H\) (это \( \displaystyle SO\)).

По теореме Пифагора для \( \displaystyle \Delta SOE\)

Но чему же равно \( \displaystyle OE\)? Это просто \( \displaystyle a\), потому что \( \displaystyle \Delta EOF\) (и все остальные тоже) правильный.

Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ №14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео мы разобрали следующие вопросы:

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь попробуй ты!

Мы рассказали тебе все о пирамидах. Не о тех, что строили инопланетяне и рептилоиды, но все же… Сделали это не хуже всяких конспирологических каналов!

Теперь ты можешь быть уверен, что у тебя есть хорошая база для решения большинства задач стереометрии. И ты не зайдешь в тупик прямо со слов «В правильном тетрадэдре PABCD…»

А теперь слово тебе. Расскажи нам, понравилась ли тебе статья? Были ли трудности?

Напиши нам ниже в комментариях!

А еще можешь задавать любые вопросы. Мы читаем все и обязательно ответим.

Источник

Пирамида

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Виды пирамид

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Источник

Пирамида

Вы будете перенаправлены на Автор24

Понятие пирамиды

Геометрическая фигура, образованная многоугольником и точкой, не лежащей в плоскости, содержащей этот многоугольник, соединенной со всеми вершинами многоугольника называется пирамидой (рис. 1).

Рисунок 1. Пирамида

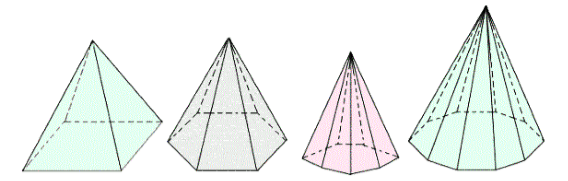
В зависимости от количества углов в основании пирамиды ее можно назвать треугольной, четырехугольной и так далее (рис. 2).

Отметим, что тетраэдр является частным случаем треугольной пирамиды.

Правильная пирамида

Пирамида, в основании которой лежит правильный многоугольник и высота пирамиды падает в его центр называется правильной пирамидой (рис. 3).

Рисунок 3. Правильная пирамида

Введем и докажем свойство правильной пирамиды.

Все боковые грани правильной пирамиды являются равнобедренными треугольниками, которые равны между собой.

Доказательство.

Готовые работы на аналогичную тему

Теорема доказана.

Введем теперь следующее определение, связанное с понятием правильной пирамиды.

Апофемой правильной пирамиды называется высота её боковой грани.

Очевидно, что по теореме 1 все апофемы равны между собой.

Площадь боковой поверхности правильной пирамиды определяется как произведение полупериметра основания на апофему.

Доказательство.

Так как, по теореме 1, все боковые стороны равны, то

Теорема доказана.

Усеченная пирамида

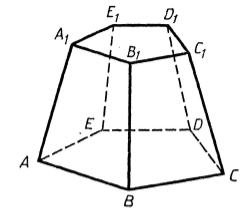
Если через обычную пирамиду провести плоскость, параллельную её основанию, то фигура, образованная между этой плоскостью и плоскостью основания называется усеченной пирамидой (рис. 5).

Рисунок 5. Усеченная пирамида

Боковыми гранями усеченной пирамиды являются трапеции.

Площадь боковой поверхности правильной усеченной пирамиды определяется как произведение суммы полупериметров оснований на апофему.

Доказательство.

Так как все боковые стороны равны, то

Теорема доказана.

Пример задачи

Найти площадь боковой поверхности усеченной треугольной пирамиды, если она получена из правильной пирамиды с основанием 6 и апофемой 4 путем отсечения плоскостью, проходящей через среднюю линию боковых граней.

Решение.

Тогда, по теореме 3, получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 04 2021

Источник

Геометрические фигуры. Правильная пирамида.

В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.

Правильная пирамида обладает следующими свойствами:

Формулы для правильной пирамиды.

Ниже указанная формула определения объема используется лишь для правильной пирамиды:

Боковое ребро правильной пирамиды находят по формуле:

где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),

n — количество сторон правильного многоугольника (основание правильной пирамиды),

h — высота правильной пирамиды (OS).

Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.

Правильная треугольная пирамида.

Формулы для правильной треугольной пирамиды.

Формула для нахождения объема правильной треугольной пирамиды:

Еще одним частным случаем правильно пирамиды является тетраэдр.

Источник