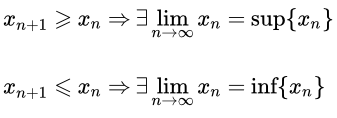Как доказать что последовательность имеет предел используя теорему вейерштрасса

Существование предела монотонной последовательности

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность имеет конечный предел, равный точной верней границе, sup для неубывающей и точной нижней границе, inf для невозрастающей последовательности.
Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности, для неубывающей и минус бесконечности, для невозрастающей последовательности.

Доказательство

1) Пусть последовательность является неубывающей ограниченной последовательностью.

Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу
.
Это означает, что:

Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу
.
Это означает следующее:

Теперь рассмотрим неограниченные последовательности.
3) Пусть последовательность является неограниченной неубывающей последовательностью.

Поскольку последовательность неубывающая, то при имеем:
.
Здесь мы также использовали (3.2).

4) Наконец рассмотрим случай, когда является неограниченной невозрастающей последовательностью.

Поскольку последовательность невозрастающая, то при имеем:
.

Пример решения задачи

Представим последовательность в виде рекуррентных формул:
,
.

Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.

Теорема Вейерштрасса об ограниченной сверху возрастающей последовательности (или ограниченной снизу убывающей последовательности) утверждает, что любая ограниченная сверху монотонно возрастающая (или ограниченная снизу монотонно убывающая) последовательность имеет предел, причём этот предел равен её точной верхней (или нижней) грани. Несмотря на прозрачность и очевидность доказательства, эта теорема оказывается очень удобной для нахождения пределов многих последовательностей или хотя бы доказательства их существования.

Доказательство и формулировка [ править | править код ]

Примечания [ править | править код ]

Литература [ править | править код ]

Зорич В. А. Математический анализ. Часть I. М.: Наука, 1981. 544 с.

Последовательность называется возрастающей (строго возрастающей) если xn+1 >= xn (xn+1 > xn) для ∀n ∈ N.

Последовательность называется убывающей (строго убывающей) если xn+1 0 найдется элемент xN ∈ такой, что a−ε N получаем a − ε 0 ∃δ > 0 : ∀x 0 0.

а) Если y0 предел функции f(x) при x → x0, то f(x) финально ограничена при x → x0;

б) Если f(x) финально постоянна при x → x0 то она имеет предел в точке x0;

в) Если f(x) в точке x0 имеет предел, то этот предел единственный.

Теорема 9. Пусть f : X → R и g : X → R две функции с общей областью определения. Если limf(x) = y0, x→x0, limg(x) = y1, x→x0, то

а) lim(f(x) ± g(x))= limf(x) ± limg(x) = y0 ± y1; x→x0

б) lim(f(x) · g(x))= limf(x) · limg(x) = y0 · y1;

Источник

Как доказать что последовательность имеет предел используя теорему вейерштрасса

`|x_n-a| oo) x_n=a` (читается: предел `x_n` при `n`, стремящемся к бесконечности, равен `a`). Последовательность, называется сходящейся, если существует число `a`, являющееся её пределом. Если такого числа `a` не существует, то последовательность называется расходящейся.

Часто в определении предела полагают число `k` натуральным. Однако, как нетрудно понять, получится эквивалентное определение.

Пусть выбрано произвольное `epsilon>0`. Нам нужно найти такое число `k`, что при всех `n>k` выполнялось бы неравенство `|x_n-c| k` имеет место неравенство `|x_n-c| oo)x_n=c`.

В разобранном примере число `k` удалось выбрать так, чтобы оно годилось сразу для всех `epsilon`. Такой случай не типичен.

Доказать, что `lim_(n->oo)1/n=0`.

Могут ли два разных числа быть пределами одной и той же последовательности?

Пусть `lim_(n->oo)x_n=a`. Имеет ли предел последовательность `(x_(n+1))`?

Пусть `lim_(n->oo)x_n=a`, `epsilon>o`. Можно ли утверждать, что найдётся такое число `k`, что `|x_n-a| k`?

Да. Поскольку `lim_(n->oo)x_n=a`, то по определению предела для любого положительного числа `alpha`, а следовательно, и для `alpha=epsilon//2`, найдётся число `k`, такое что `|x_n-a|k`.

Сформулируем необходимое условие существования предела.

Если последовательность имеет предел, то она ограничена.

Доказать, что последовательность `x_n=(-1)^n` не имеет предела.

Предположим противное, т. е. какое-то число `a` является пределом этой последовательности. Тогда для `epsilon=1` найдётся такое число `k`, что `|x_n-a| k`. Пусть номер `N>k`, тогда `|x_N-a| oo)y_n!=0`). При этом

Ограничимся доказательством пункта 2. Фиксируем произвольное `epsilon>0`. Нам нужно показать, что существует такое число `k`, что `|x_ny_n-ab| k`. По теореме 2.1 последовательности `(x_n)` и `(y_n)` ограничены; тем самым найдётся такое `C>0`, что `|x_n| k_1`, а также число `k_2` такое, что `|y_n-b| k_2`. Если положить `k=max`, то при `n>k` имеем:

`|x_ny_n-ab| oo)cx_n=clim_(n->oo)x_n` для любого `cinR`.

В самом деле, рассмотрим последовательность `y_n=c`. Поскольку `lim_(n->oo)y_n=c` (пример 2.1), то по пункту 2 теоремы 2.2

Показать, что `lim_(n->oo) 1/(n^2)=0`.

Поскольку `lim_(n->oo) 1/n=0`, то по пункту 2 теоремы 2.2

`lim_(n->oo) 1/(n^2)=lim_(n->oo) 1/n*lim_(n->oo) 1/n=0`.

Теорему 2.2 можно обобщить на произвольное (конечное) число слагаемых (сомножителей). В частности, `lim_(n->oo)1/n^m=0` для любого `m inN`.

Обозначим дробь, стоящую под знаком предела, через `x_n`. В числителе и знаменателе `x_n` стоят последовательности, не являющиеся ограниченными (доказывается аналогично примеру 1.6). По теореме 2.1 они не имеют предела и теорема о пределе частного (теорема 2.2 3)) «напрямую» здесь неприменима. Поступим следующим образом: поделим числитель и знаменатель на наибольшую степень `n`. По формулам сокращённого умножения `(n+2)^3-n(n-1)^2=8n^2+11n+8`, так что `x_n` можно переписать в виде:

Теперь в числителе и знаменателе `x_n` стоят сходящиеся последовательности:

По пункту 3 теоремы 2.2

Следующее полезное свойство пределов известно под названием теоремы о «зажатой» последовательности.

Для данного `epsilon>0` существует такое число `k_1`, что члены `x_n` лежат в интервале `(a-epsilon, a+epsilon)` при всех `n>k_1`, и существует такое число `k_2`, что члены `z_n` лежат в интервале `a-epsilon;a+epsilon)` при всех `n>k_2`. Положим `k=max`. Тогда при `n>k` одновременно `x_n in(a-epsilon;a+epsilon)` и `z_n in(a-epsilon;a+epsilon)` и, следовательно, `a-epsilon oo)x_n=1`.

Попробуем «зажать» `x_n` между членами последовательностей, сходящихся к одному и тому же числу, и применим теорему 2.3.

`sqrt(n^2+n) 1/(n+1) iff n/(sqrt(n^2+n))>n/(n+1)`.

Учитывая `n/(sqrt(n^2+1)) oo)n/(n+1)=1` и `lim_(n->oo)1=1`, по теореме 2.3 `lim_(n->oo)x_n=1`.

Если для любого `n inN`, `n>=n_0` выполняется неравенство `a_n oo)a_n=a`, `lim_(n->oo)b_n=b`, то `a b`. По определению предела для `epsilon=(a-b)/2` найдутся такие `k_1`, `k_2`, что для `n>k_1` выполняется `|a_n-a| k_2` выполняется `|b_n-b| k` имеем `b_n oo)1/n=0`.

В теории пределов важную роль играет следующий факт.

Всякая монотонная ограниченная последовательность имеет предел.

Эта теорема эквивалентна свойству полноты множества действительных чисел. Образно говоря, свойство полноты означает, что числовая ось является «сплошным» множеством, множеством без «дырок».

Источник

Предел последовательности. Теорема Вейерштрасса.

Число A называется пределом последовательности x_n, если ∀U(A) ∃ N: ∀ n > N x_n ∊ U(A).

Теорема: Если f непрерывна на [a, b], то она достигает на нем своей верхней и нижней грани.

Билет №6

Бесконечно малые и бесконечно большие функции, связь между ними

Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.

Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых |x – a| 0 такое, что как только |x – a| 1/ ε. Но тогда для тех же x .

Примеры.

1. Ясно, что при x→+∞ функция y=x 2 +1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция – бесконечно малая при x→+∞, т.е. .

2. .

Билет №7

Свойства бесконечно малых функций

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Основные свойства:

1) Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство.Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где и . Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a| 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁>0, что при |x – a| 0, что при |x – a| 0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)| 2 ≠0.

Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

, то .

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Теорема Вейерштрасса

Любая монотонная и ограниченная последовательность

\(\ \left\\right\> \)имеет предел.

Эта теорема может быть сформулирована для возрастания последовательностей следующим образом:

Если последовательность \(\ \left\\right\> \)возрастает и ограничена сверху, то предел этой последовательности является ее точной верхней границей:

Для нисходящих последовательностей:

Если последовательность \(\ \left\\right\> \)убывает и ограничена ниже, то предел этой последовательности равен ее точной нижней границе:

Комментарий. Теорема Вейерштрасса на пределе монотонной последовательности является теоремой о существовании предела последовательности и не дает каких-либо методов для нахождения этого предела.

Примеры решения проблем

Докажите, что последовательность \(\ \left\\right\>=\left\<\frac<3>\right\> \)имеет предел и находит ее.

Эта последовательность ограничена снизу нулем, так как для любого натурального \(\ n, x_=\frac<3>>0 \).

Затем мы исследуем заданную последовательность для монотонности, для чего рассмотрим разность ее соседних членов:

Оцените полученную разницу: для любого натурального \(\ \Pi \)

Следовательно, последовательность \(\ \left\\right\> \) монотонно убывает, то, согласно теореме Вейерштрасса, она имеет предел. Найди это:

Последовательность \(\ \left\\right\>=\left\<\frac<3>\right\> \)сходится и ее предел равен нулю.

Чтобы исследовать последовательность \(\ a_=\sqrt<6+a_> \) для сходимости, если \(\ a_<1>=2 \)

Предположим, что предел этой последовательности существует, то есть:

Приравнивая правые части двух последних равенств, приходим к уравнению для а:

Решая его, мы получаем

\(\ a^<2>-a-6=0 \Rightarrow(a-3)(a+2)=0 \Rightarrow a_<1>=3, a_<2>=-2 \)

Значение \(\ a_<2>=-2 \) непригодно, так как предел неотрицательных чисел не может быть отрицательным числом. Поэтому, если предел данной последовательности существует, то он равен 3.

Докажем существование предела. Для этого, согласно теореме Вейерштрасса, последовательность должна быть монотонной и ограниченной. Рассмотрим разницу

Источник