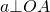Как доказать что прямая является касательной
Касательная к окружности
Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
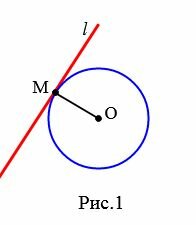
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.
 |
Свойство касательной
Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.
Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.
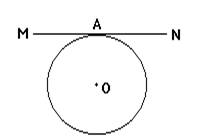
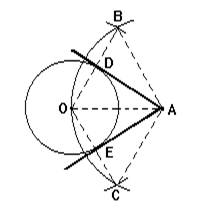
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.
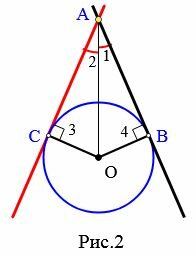 |
Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.
Теорема, обратная теореме о свойстве касательной
Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.
Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).
Построение касательной к окружности
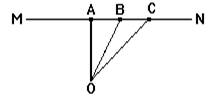
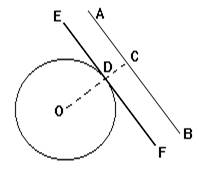
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).
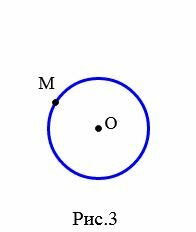 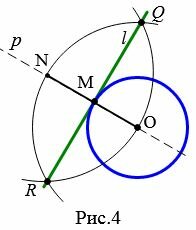 |
Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.
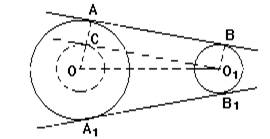
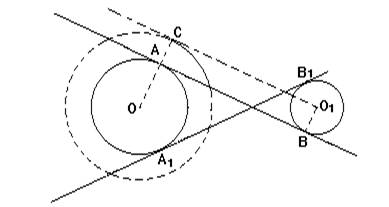
Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).
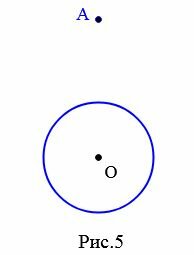 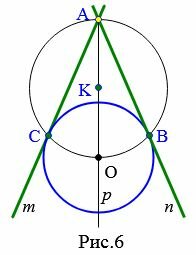 |
Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.
Касательная к окружности
Что такое касательная к окружности? Каково взаимное расположение касательной и радиуса?
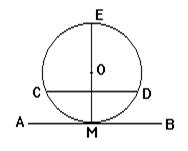
a — касательная,
A — точка касания
Касательная к окружности — это прямая, которая имеет с окружностью только одну общую точку — точку касания.
(Свойство касательной к окружности).
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано: окружность (O;R), R=OA,
a — касательная к окружности,
Доказательство проведем методом от противного.
Предположим, что радиус OA и прямая a не перпендикулярны.
Опустим из точки O на прямую a перпендикуляр OB.
Тогда OA — наклонная, проведенная из точки O на прямую a.
По свойству перпендикуляра и наклонной, любая наклонная больше перпендикуляра. Значит, OA>OB.
Получается, расстояние от точки O до прямой a — длина перпендикуляра OB — меньше радиуса. Из этого следует, что прямая a и окружность имеют две общие точки.
Противоречие получили, так как предположили, что радиус OA и касательная a не перпендикулярны. Значит, касательная перпендикулярна к радиусу, проведенному в точку касания:
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Решение
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
Для наглядности изобразим графически.
Решение
Необходимо продифференцировать функцию. Имеем, что
Вычисляем соответствующие значения функции
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
Другое уравнение имеет два действительных корня, тогда
Перейдем к нахождению значений функции. Получаем, что
Возможно существование бесконечного количества касательных для заданных функций.
Решение
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
Ответ: необходимы уравнения запишутся как
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Данное равенство может быть записано как объединение двух функций:
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Касательная к эллипсу
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
Решение
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
Графически касательные обозначаются так:
Касательная к гиперболе
Гипербола может быть представлена в виде двух объединенных функций вида
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
Ответ: уравнение касательной можно представить как
Наглядно изображается так:
Касательная к параболе
Графически изобразим как:
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
Отсюда определим значение х для точек касания.
Первая функция запишется как
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
Ответ: уравнение касательной принимает вид
Касательная к окружности
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.