Как доказать что прямые параллельны в разных плоскостях

Стереометрия. Страница 2

Главная > Учебные материалы > Математика: Стереометрия. Страница 2

1.Параллельность прямых в пространстве. 2.Признак параллельности прямых. 3.Признак параллельности плоскостей. 4.Свойства параллельных плоскостей. 5.Примеры.

1. Параллельность прямых в пространстве

Теорема. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Доказательство. Пусть b данная прямая и точка А, не лежащая на данной прямой. Проведем через точку А и прямую b плоскость α. А через точку А прямую a, параллельную прямой b. (Рис.1)

Допустим, что существует другая прямая а’, параллельная прямой b и проходящая через точку А. Тогда через них можно провести плоскость β. Отсюда следует, что через точку А и прямую b можно провести две плоскости. А это невозможно согласно теореме о единственности существования плоскости, проведеной через прямую и не лежащую на ней точку. Таким образом, плоскости α и β совпадают. А следовательно, согласно аксиоме, прямые а и a’ совпадают также.

Рис. 1 Параллельность прямых в пространстве.

2.Признак параллельности прямых

Теорема. Две прямые, параллельные третьей прямой, параллельны.

Доказательство. Пусть прямые а и b лежат в разных плоскостях и параллельны прямой с. Доказать, что прямые а и b параллельны между собой. (Рис.2)

Рис.2 Признак параллельности прямых

3. Признак параллельности плоскостей

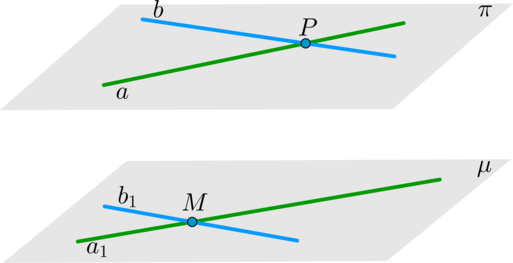
Теорема: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Доказательство.

а ∈ α, γ.
а 1 ∈ β, γ.
с ∈ α, β,γ

т.е. плоскости α и γ пересекаются по двум прямым а и с, а плоскости β и γ пересекаются по прямым а 1 и с.

Рис. 3 Признак параллельности плоскостей.

Согласно аксиоме стереометрии, это невозможно, т.к. две плоскости могут пересекаться только по одной прямой. И следовательно, наше предположение неверно. Плоскости α и β не пересекаются, они параллельны.

4. Свойства параллельных плоскостей

Теорема: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

Доказательство.

Пусть даны две параллельные плоскости α и β (Рис.4). Плоскость γ пересекает их по прямым а и b.

Рис. 4 Свойства параллельных плоскостей.

5. Пример 1

Докажите, что если прямые АВ и CD скрещивающиеся, то прямые АС и BD тоже скрещиваются.

Доказательство:

Пусть даны две скрещивающиеся прямые АВ и CD. Проведем через прямую АВ и точку С плоскость α (Рис.5). Так как прямые АВ и CD скрещивающиеся, то прямая CD не лежит в плоскости α, а пересекает ее в одной точке С.

Отсюда следует, что точка D не принадлежит плоскости α. Она лежит вне ее.

Таким образом, если мы проведем прямую АС, то она полностью будет принадлежать плоскости α, так как две ее точки А и С принадлежат плоскости α.

А прямая BD не будет принадлежать плоскости α, так как точка D не принадлежит плоскости α. Прямая BD будет пересекать плоскость α в одной точке В.

Отсюда можно сделать вывод, что прямая АС не может пересекать прямую BD, так как прямая АС полностью принадлежит плоскости α. А прямая BD имеет только одну общую точку с плоскостью α, точку В. Но так как точка В не лежит на прямой АС, следовательно, прямые АС и BD не пересекаются. Они являются скрещивающимися.

Рис.5 Задача. Докажите, что если прямые АВ и CD скрещивающиеся.

Пример 2

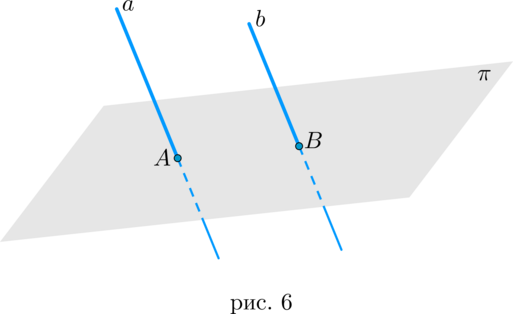
Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем плоскость α через точки A, D, C и плосксоть α’ через точки А, В, С (Рис.6). Точки P, S, F, E являются серединами отрезков AB, BC, AD и CD соответственно. Необходимо доказать, что прямая PS параллельна прямой FE.

Рассмотрим треугольник АВС. Он полностью лежит в плоскости α’, так как три его вершины лежат в данной плоскости по построению. Отрезок PS представляет собой среднюю линию треугольника, которая параллельна АС.

Теперь рассмотрим треугольник АСD. Он полностью лежит в плоскости α, так как три его вершины лежат в данной плоскости по построению. Отрезок FE представляет собой среднюю линию треугольника, которая также параллельна АС.

Отсюда можно сделать вывод: если две прямые PS и FE параллельны третьей прямой АС, то они параллельны и между собой. И равны половине основанию АС. Таким образом, PSEF представляет собой параллелограмм.

Рис.6 Задача. Точки А, В, С, D не лежат в одной плоскости.

Пример 3

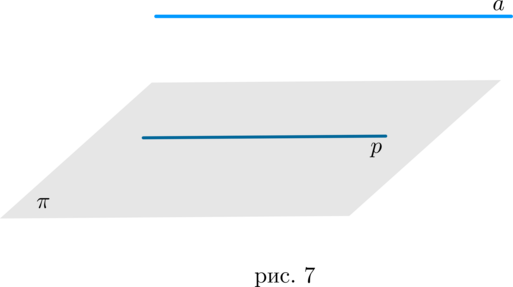
Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и ВС, АС и BD, AD и BC пересекаются в одной точке.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем отрезки EP, VS, FT, которые соединят середины сторон AB и CD, BC и AD, AC и BD соответственно (Рис.7).

Из предыдущей задачи нам известно, что четырехугольник EVPS, вершины которого являются серединами отрезков АВ, ВС, СD и AD, есть параллелограмм, у которого EP и VS диагонали. Эти диагонали пересекаются в точке О и делятся этой точкой пополам.

Так как у отрезка VS середина одна, т.е. точка О, то все три диагонали EP, VS и FT пересекаются в этой точке.

Рис.7 Задача. Даны четыре точки А, В, С, D, не лежащие в одной плоскости.

Пример 4

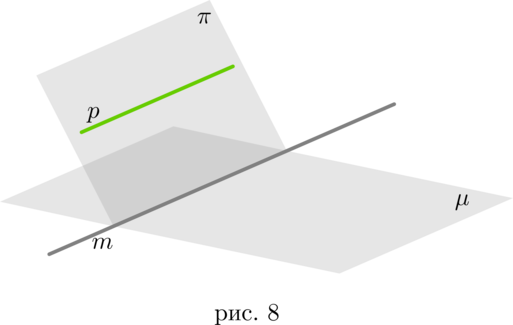
Докажите, что если две плоскости, пересекающиеся по прямой а, пересекают плоскость α по параллельным прямым, то прямая а параллельна плоскости α.

Доказательство:

Пусть даны две плоскости β и γ, пересекающиеся по прямой а (Рис.8). Эти плоскости пересекают плоскость α по параллельным прямым b и с. Необходимо доказать, что прямая а параллельна плоскости α.

Рис.8 Задача. Докажите, что если две плоскости, пересекающиеся по прямой а.

Пример 5

Докажите, что если четыре прямые, проходящие через точку О, пересекают плоскость α в вершинах параллелограмма, то они пересекают любую плоскость, параллельную α и не проходящую через точку О, тоже в вершинах параллелограмма.

Доказательство:

Пусть даны четыре прямые, проходящие через точку О, ОА, ОВ, ОС и OD (Рис.9). Они пересекают плоскость α в точках А, В, С и D соответственно. Проведем плоскость α’, параллельную плоскости α. Тогда прямые ОА, ОВ, ОС и OD пересекут плоскость α’ в точках A’B’C’D’.

Проведем плоскость β через точки А, В, A’, B’. Тогда прямые АВ и A’B’ не пересекаются, так как это прямые пересечения двух параллельных плоскостей α и α’ с секущей плоскостью β.

Отсюда следует, что прямые ВС и В’С’, CD и C’D’, AD и A’D’ параллельны. А так как АВ параллельна CD, а ВС параллельна AD, то следовательно, А’В’ параллельна C’D’, а В’С’ параллельна A’D’.

Таким образом, A’B’C’D’ также является параллелограммом.

Рис.9 Задача. Докажите, что если четыре прямые, проходящие через точку А.

Источник

Введение в стереометрию. Параллельность

Важные аксиомы стереометрии

1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Таким образом, любая плоскость однозначно задается тремя точками, не лежащими на одной прямой: \(\pi=(ABC)\) (рис. 1).

Заметим, что плоскость обычно изображают в виде внутренности параллелограмма. Почему? Посмотрите, например, сбоку на стол. В виде какой фигуры выглядит столешница?

Следствия из аксиом

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна (рис. 4).

2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 5).

Доказательство

Определения

Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

Следствие 1

Через две параллельные прямые проходит плоскость, и притом только одна.

Теорема 1

Доказательство

Теорема 2

Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Доказательство

Теорема 3: о параллельности трех прямых

Доказательство

Определение

Существует три вида взаимного расположения прямой и плоскости:

1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости) — рис. 4;

2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость) — рис. 6;

3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).

Теорема 4: признак параллельности прямой и плоскости

Доказательство

Следствие 2

Доказательство

Следствие 3

Определение

Существует три типа взаимного расположения плоскостей в пространстве: совпадают (имеют три общие точки, не лежащие на одной прямой), пересекаются (имеют общие точки, лежащие строго на одной прямой), и не имеют общих точек.

Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.

Теорема 5: признак параллельности плоскостей

Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

Доказательство

Следствие 4

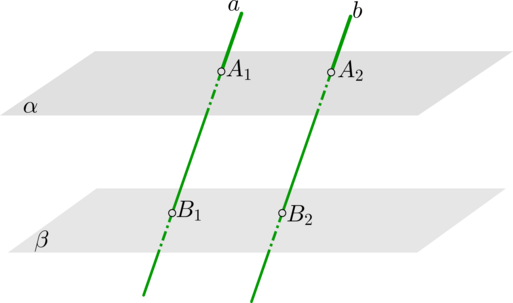
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

Следствие 5

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны:

\[\alpha\parallel \beta, \ a\parallel b \Longrightarrow A_1B_1=A_2B_2\]

Источник

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости

Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.

Ответ: прямая с плоскостью параллельны.

Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.

Ответ: не параллельны.

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Ответ: прямая и плоскость параллельны.

Источник

Определение параллельных прямых в пространстве

Понятие о параллельных прямых

Прямые \(a\) и \(b\) являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются.

Если рассмотреть примеры, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочее. Таких примеров из реального мира можно привести очень много.

Другими вариантами прямых, расположенных в 3D-пространстве, есть их скрещивание и пересечение. Пересекающимися есть прямые, имеющие общую точку, она же и есть точкой пересечения. Скрещивающимися есть прямые, расположенные в разных плоскостях и не параллельные между собой.

Есть ряд теорем, описывающих поведение параллельных прямых в пространстве. Рассмотрим их подробнее.

Теоремы о параллельности двух прямых

Свойства параллельных прямых в пространстве

Некоторые свойства пересекаются с вышеизложенными теоремами, но все же рассмотрим их все:

Не нашли что искали?

Просто напиши и мы поможем

В соответствии с аксиомой планиметрии, при пересечении одной из параллельных прямых третьей прямой, вторая так же будет ее пересекать.

Пример задачи о параллельных прямых

При совпадении прямых или если они параллельны их направляющие векторы \(s_1\) и \( s_2\) будут коллинеарными, таким образом, их координаты будут иметь следующее соотношение:

Для того, чтобы найти направляющие вектора, воспользуемся каноническими уравнениями, таким образом для прямой a вектор \(s_1\) будет равен <1;3;-2>.

Для прямой b найдем направляющий вектор при помощи произведения нормальных векторов плоскостей, на которых он расположен:

Таким образом, соблюдается вышеуказанное условие, значит эти прямые либо параллельны, либо совпадают. Необходимо определить каковыми именно они являются: параллельны или совпадают. Возьмем некую точку \(K\) с координатами (1;2;-1), находящуюся на прямой a, и подставим ее координаты в уравнение прямой \(b\) :
1-2+1+1=0;1=0,

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник