Как доказать что прямые пересекаются в пространстве

Точка пересечения прямых в пространстве онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Точка пересечения прямых в пространстве − теория, примеры и решения

1. Точка пересечения прямых в пространстве, заданных в каноническом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂:

,

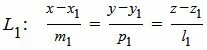(1)

,

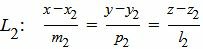(2)

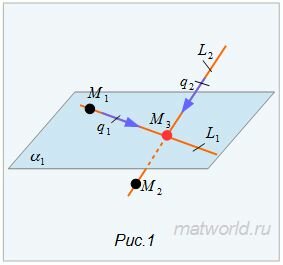
Найти точку пересечения прямых L₁ и L₂ (Рис.1).

Запишем уравнение (1) в виде системы двух линейных уравнений:

Сделаем перекрестное умножение в уравнениях (3) и (4):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Аналогичным образом преобразуем уравнение (2):

Запишем уравнение (2) в виде системы двух линейных уравнений:

Сделаем перекрестное умножение в уравнениях (7) и (8):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:

2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂ в параметрическом виде:

Задачу нахождения нахождения точки пересечения прямых L₁ и L₂ можно решить разными методами.

Метод 1. Приведем уравнения прямых L₁ и L₂ к каноническому виду.

Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:

Так как левые части уравнений (14) равны, то можем записать:

Аналогичным образом приведем уравнение прямой L₂ к каноническому виду:

Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямых L₁ и L₂ решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:

Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).

3. Точка пересечения прямых в пространстве, заданных в разных видах.

Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.

4. Примеры нахождения точки пересечения прямых в пространстве.

Пример 1. Найти точку пересечения прямых L₁ и L₂:

Представим уравнение (20) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (22) и (23):

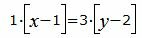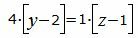Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

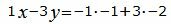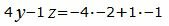Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (7) и (8)

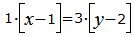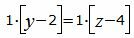Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

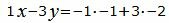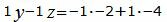Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

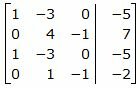Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1:

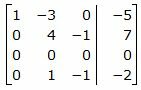Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:

Сделаем перестановку строк 3 и 4.

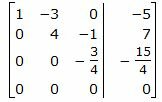Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:

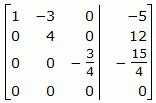Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:

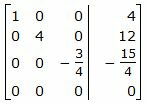Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

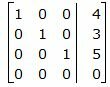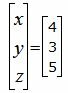Ответ. Точка пересечения прямых L₁ и L₂ имеет следующие координаты:

Пример 2. Найти точку пересечения прямых L₁ и L₂:

Приведем параметрическое уравнение прямой L₁ к каноническому виду. Выразим параметр t через остальные переменные:

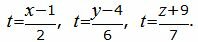Из равентсв выше получим каноническое уравнение прямой:

Представим уравнение (33) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (34 и (35):

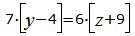Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

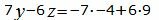Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (38) и (39)

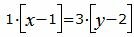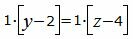Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

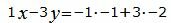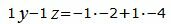Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:

Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:

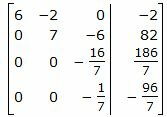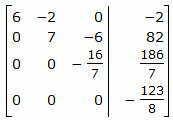Из расширенной матрицы восстановим последнюю систему линейных уравнений:

Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L₁ и L₂ не пересекаются. То есть они или параллельны, или скрещиваются.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник

Взаимное расположение прямых в пространстве

Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями

где — точки, принадлежащие прямым и соответственно, a — направляющие векторы (рис.4.34). Обозначим через вектор, соединяющий заданные точки.

Перечисленным выше случаям взаимного расположения прямых и соответствуют следующие признаки:

– прямые и скрещивающиеся векторы не компланарны;

– прямые и пересекаются векторы компланарны, а векторы не коллинеарны;

– прямые и параллельные векторы коллинеарны, а векторы не коллинеарны;

– прямые и совпадают векторы коллинеарны.

Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:

Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:

– прямые и скрещивающиеся определитель отличен от нуля;

– прямые и пересекаются определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е.

– прямые и параллельные вторая и третья строки определителя пропорциональны, т.е. а первые две строки не пропорциональны, т.е.

– прямые и совпадают все строки определителя пропорциональны, т.е.

Расстояние между параллельными прямыми

Найдем расстояние между параллельными прямыми, заданными каноническими уравнениями (рис.4.35)

где — произвольные точки на прямых и соответственно, а координаты направляющих векторов прямых пропорциональны:

Расстояние между скрещивающимися прямыми

Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.

Найдем расстояние между скрещивающимися прямыми, заданными каноническими уравнениями

где — произвольные точки на прямых и соответственно.

Искомое расстояние равно высоте параллелепипеда, построенного на векторах (рис.4.36), т.е.

— смешанное и векторное произведения векторов. Как показано выше, прямые и скрещивающиеся тогда и только тогда, когда векторы некомпланарные, т.е.

Отсюда следует, что вторая и третья строки не пропорциональны. Поэтому векторы неколлинеарные, т.е. и знаменатель в правой части (4.38) отличен от нуля.

Угол между прямыми

Угол между прямыми определяется как угол между их направляющими векторами. Поэтому величина острого угла между прямыми

вычисляется по формуле

Решение. Каноническое уравнение оси абсцисс имеет вид так как ось проходит через точку а — ее направляющий вектор. Каноническое уравнение прямой получено в примере 4.15,»а»:

Полагая по формуле (4.38) получаем:

Острый угол находим по формуле (4.39):

Взаимное расположение прямой и плоскости

Возможны три случая взаимного расположения прямой и плоскости:

– прямая и плоскость пересекаются, т.е. имеют одну общую точку;

– прямая и плоскость параллельны, т.е. не имеют общих точек;

– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.

Получим признаки для всех этих случаев. Пусть прямая и плоскость заданы уравнениями:

т.е. прямая проходит через точку коллинеарно вектору а плоскость перпендикулярна вектору

Перечисленным выше случаям взаимного расположения прямой и плоскости соответствуют следующие признаки:

– прямая и плоскость пересекаются векторы и не ортогональны (рис.4.37,а);

– прямая и плоскость параллельны векторы и ортогональны, а точка не принадлежит плоскости (рис.4.37,б);

– прямая лежит в плоскости векторы и ортогональны, а точка принадлежит плоскости (рис.4.37,в).

Учитывая свойство скалярного произведения векторов получаем:

– прямая и плоскость пересекаются ;

– прямая и плоскость параллельны

– прямая лежит в плоскости

Угол между прямой и плоскостью

Отсюда, например, следует полученное ранее необходимое условие параллельности прямой и плоскости.

Источник

Стереометрия. Страница 3

Главная > Учебные материалы > Математика: Стереометрия. Страница 3

1.Перпендикулярность прямых в пространстве. 2.Признак перпендикулярности прямой и плоскости. 3.Теорема о трех перпендикулярах. 4.Признак перпендикулярности плоскостей. 5.Расстояние между скрещивающимися прямыми. 6.Примеры.

1. Перпендикулярность прямых в пространстве

Теорема. Если две пересекающиеся прямые параллельны двум перпендикулярным прямым, то они перпендикулярны и между собой.

Рис. 1 Перпендикулярность прямых в пространстве.

2.Признак перпендикулярности прямой и плоскости

Теорема. Прямая, перпендикулярная двум пересекающимся прямым на плоскости, перпендикулярна данной плоскости.

Доказательство. Пусть прямые k и b две пересекающиеся прямые на плоскости α. Прямая а перпендикулярна прямым k и b. Доказать, что прямая а перпендикулярна плоскости α. (Рис.2)

Проведем произвольную прямую х от точки А и прямую АВ, которая пересечет прямые k и b в точках К и В на плоскости α. Отложим на прямой а два равных отрезка в разные стороны АА’ и AA». Тогда треугольники АА’K и AA»K будут равны по двум сторонам и углу между ними. Так же как и треугольники АА’В и AA»В. Отсюда следует, что треугольники А’BK и А»BK равны по третьему признаку равенства треугольников. И следовательно, треугольники А’BE и A»BE равны, т.к. одна сторона у них общая ВЕ, стороны А’B и А»B равны из предыдущих рассуждений. Углы между этими сторонами также равны. Следовательно мы приходим к выводу, что треугольники А’AE и A»AE равны по трем сторонам. АЕ является медианой, биссектрисой и высотой, так как стороны А’Е и A»Е у них равные. И следовательно, угол между сторонами АА’ и АЕ равен 90°. Это значит, что прямая а перпендикулярна плоскости α.

Рис.2 Признак перпендикулярности прямой и плоскости

3. Теорема о трех перпендикулярах

Теорема: если прямая, проведенная на плоскости и проходящая через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и наклонной.

Доказательство.

Проведем прямую через основание наклонной AD и параллельную прямой СВ. Тогда прямая AD также перпендикулярна плоскости α и соответственно прямой а. Проведем плоскость β через прямые АD и CB. Тогда, если прямая а перпендикулярна проекции наклонной АВ, то она перпендикулярна плоскости β. А следовательно, любой прямой в этой плоскости, т.е. самой наклонной АС.

Следует отметить, что верно и обратное утверждение. Если прямая, проведенная на плоскости через основание наклонной ей перпендикулярна, то она перпендикулярна и проекции наклонной на эту плоскость.

Рис. 3 Теорема отрех перпендикулярах.

4. Признак перпендикулярности плоскостей

Теорема: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость перпендикулярна их прямой пересечения и пересекает их по перпендикулярным прямым.

Пусть даны две плоскости α и β, которые пересекаются по прямой с (Рис.4). Проведем плоскость γ, которая пересекает плоскости α и β по прямым а и b. Плоскость γ перпендикулярна прямой с. Прямые а и b также перпендикулярны прямой с. Следовательно плоскости α и β перпендикулярны.

Если взять другую плоскость, параллельную плоскости γ, например плоскость γ’, которая пересекает прямую с под прямым углом, она пересечет плоскости α и β по прямым a’ и b’, которые будут параллельны прямым а и b. По теореме о перпендикулярности прямых в пространстве прямые a’ и b’ также будут перпендикулярны, как и прямые а и b. Что и требовалось доказать.

Рис. 4 Признак перпендикулярности плоскостей.

Теорема: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Проведем через точку А на плоскости α прямую b, перпендикулярную прямой а. Через прямые b и с проведем плоскость γ. Она перпендикулярна прямой а, так как прямая а перпендикулярна двум прямым b и с. Тогда плоскость β пересекает две плоскости α и γ по двум перпендикулярным прямым а и с. И пересекает прямую пересечения b под прямым углом. Следовательно плоскости α и β перпендикулярны.

Рис. 4.1 Перпендикулярность плоскостей.

5. Расстояние между скрещивающимися прямыми

Теорема. Две скрещивающиеся прямые имеют только один общий перпендикуляр, который также является перпендикуляром между параллельными плоскостями, проведенными через эти прямые.

Доказательство. Пусть а и b две скрещивающиеся прямые (Рис.5). Проведем через них две плоскости α и β, параллельные друг другу. А от прямой а проведем перпендикуляры на плоскость β. Таким образом, получим плоскость γ, которая перпендикулярна обоим плоскостям α и β и пересекает плоскость β по прямой a’. Прямые а и a’ параллельны. Прямая a’ пересекает прямую b в точке А. Следовательно, один из перпендикуляров, проведенных от каждой точки прямой а на плоскость β, т.е. отрезок АВ и есть общий перпендикуляр между прямыми а и b.

Допустим, что существует еще один общий перпендикуляр между прямыми а и b это CD. Тогда два перпендикуляра пересекают прямые а и b в точках А,В,С,D, которые в свою очередь параллельны между собой. Следовательно через них можно провести плоскость. А в этой плоскости лежат и две прямые а и b, которые также будут параллельны между собой. А это противоречит условию, т.к. прямые а и b являются скрещивающимися. Следовательно у двух скрещивающихся прямых может быть только один общий перпендикуляр.

Отсюда следует, что расстояние между двумя скрещивающимися прямыми равно длине их общего перпендикуляра.

Рис. 5 Расстояние между скрещивающимися прямыми.

5. Пример 1

Докажите, что через точку, не лежащую в данной плоскости, можно провести только одну прямую, перпендикулярную данной плоскости.

Доказательство:

Пусть дана плоскость α и точка А, не лежащая на данной плоскости. Проведем в плоскости α две пересекающиеся прямые d и c. А через их точку пересечения О проведем прямую f, перпендикулярную d и с (Рис.6).

Тогда по признаку перпендикулярности прямой и плоскости, прямая f будет перпендикулярна плоскости α. Теперь проведем прямую АВ, параллельную прямой f. Тогда АВ будет перпендикуляром к плоскости α также.

Возьмем на прямой b произвольную точку С и проведем в плоскости β прямую а, перпендикулярную прямой b. Тогда согласно аксиоме, (через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной), прямая АВ, параллельная прямой а, единственная. Т.е. перпендикуляр АВ к прямой b. Таким образом, перпендикуляр АВ единственный.

Рис.6 Задача. Докажите, что через точку, не лежащую в данной плоскости.

Пример 2

Через точку А прямой а проведены перпендикулярные ей плоскость β и прямая b. Докажите, что прямая b лежит в плоскости β.

Доказательство:

Пусть дана прямая а, перпендикулярные ей плоскость β и прямая b. Плоскость β и прямая b проходят через точку А прямой а (Рис.7). Необходимо доказать, что прямая b принадлежит плоскости β.

Проведем через две пересекающиеся прямые а и b плоскость α. Тогда две плоскости α и β пересекаются по прямой b’. Так как точка А принадлежит обоим плоскостям, то она лежит на прямой b’.

Таким образом, получается, что через точку А проходят две прямые b и b’, которые принадлежат плоскости α. Плоскость β перпендикулярна прямой а по условию задачи. А следовательно, прямая а перпендикулярна прямой b’. Отсюда следует, что через точку А проходят две прямые, лежащие в одной плоскости α, и перпендикулярные прямой а. А это невозможно. Так как через точку прямой можно провести только одну перпендикулярную ей прямую. Следовательно, прямые b и b’ совпадают. А отсюда следует, что прямая b полностью принадлежит плоскости β.

Рис.7 Задача. Через точку А прямой а проведены перпендикулярные ей плоскость β.

Пример 3

Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от вершин треугольника.

Доказательство:

Пусть дан треугольник АВС и описанная вокруг него окружность с центром в точке О. Прямая а перпендикулярна плоскости треугольника (Рис.8). Необходимо доказать, что каждая точка прямой а равноудалена от вершин треугольника А, В и С.

Рассмотрим треугольник АВС. Вокруг него описана окружность с центром в точке О, поэтому отрезки АО, ВО и СО равны как радиусы. Теперь возьмем произвольную точку Х на прямой а. Так как прямая а перпендикулярна плоскости треугольника, то треугольники АОХ, ВОХ и СОХ равны по первому признаку равенства треугольников, т.е. по двум сторонам и углу между ними. У них сторона ОХ общая, а стороны АО, ВО и СО равны как радиусы. И углы между этими сторонами составляют 90°.

Отсюда можно сделать вывод, что стороны АХ, ВХ и СХ этих треугольников равны. Т.е. расстояние от вершин треугольника АВС до любой точки прямой а одинаковые.

Рис.8 Задача. Через центр описанной около треугольника окружности.

Пример 4

Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная его плоскости. Расстояние от точки К до других вершин прямоугольника равны 9 см, 13 см и 15 см. Найдите АК.

Решение:

Пусть дан прямоугольник АВСD и прямая АК, перпендикулярная плоскости прямоугольника. ВК = 9 см, СК = 15 см, DK = 13 см (Рис.9). Необходимо найти АК.

Так как прямая АК перпендикулярна плоскости прямоугольника, то она перпендикулярна прямым АВ, AD и АС. Отсюда следует, что по теореме Пифагора можно составить следующие соотношения:

АВ 2 + AD 2 + AK 2 = CK 2

AK 2 = 25 или АК = 5 см.

Рис.9 Задача. Через вершину А прямоугольника ABCD.

Пример 5

Через основание трапеции проведена плоскость, отстоящая от другого основания на расстоянии 2 см. Найдите расстояние от точки пересечения диагоналей трапеции до этой плоскости, если основания трапеции относятся как 4:5 (верхнее к нижнему).

Решение:

Пусть дана трапеция АВСD. Плоскость α проведена через основание AD (Рис.10). ВС / AD = 4 / 5. Необходимо найти OO’.

Рассмотрим треугольники ВОС и AOD. Они подобны по трем углам. Коэффициент подобия составляет 4 / 5. Отсюда следует, что высоты ОЕ и ОF также относятся как 4 / 5.

Теперь рассмотрим треугольники FOO’ и FEE’. Они также подобны по трем углам. Коэффициент подобия у них составляет 5 / 9.

Таким образом, OO’ = EE’ 5 / 9 = 2*5 / 9 = 10 / 9 см.

Рис.10 Задача. Через основание трапеции проведена плоскость.

Источник