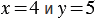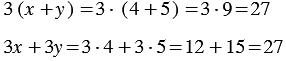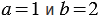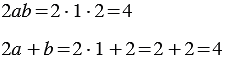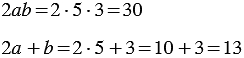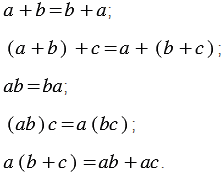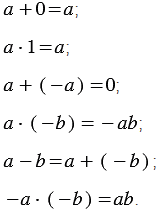Как доказать что равенство является тождеством
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
и 
Найдем их значения при 
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных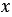 
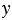
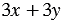
и 
значения выражений и равны.
2) 
Найдем их значения при 
Мы получили один и тот же результат. Однако, можно указать такие значения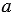 
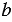
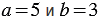
и 
, при которых значения этих выражений не будут иметь равные значения. Например, если 
, то
Мы получили разные результаты.
Следовательно, выражения и являются тождественно равными, а выражения не являются тождественно равными.
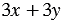
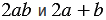
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство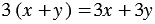 
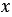
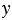
— тождество, т.к. оно верно при любых значениях и .
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 
, мы преобразовали выражение 
в выражение 
.
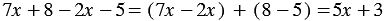
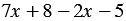
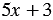
2) 
, мы преобразовали выражение 
в выражение 
.
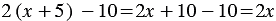
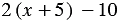
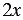
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство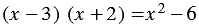 
не является тождеством.
Решение: Приведем контрпример. Если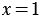 
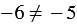
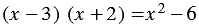
, то
, следовательно, равенство не является тождеством.
Поделись с друзьями в социальных сетях:
Тождества: определение, обозначение, примеры
Начнем разговор о тождествах, дадим определение понятия, введем обозначения, рассмотрим примеры тождеств.
Что представляет собой тождество
Начнем с определения понятия тождества.
Тождество представляет собой равенство, которое верно при любых значениях переменных. Фактически, тождеством является любое числовое равенство.
По мере разбора темы мы можем уточнять и дополнять данное определение. Например, если вспомнить понятия допустимых значений переменных и ОДЗ, то определение тождества можно дать следующим образом.
Тождество – это верное числовое равенство, а также равенство, которое будет верным при всех допустимых значениях переменных, которые входят в его состав.
Про любые значения переменных при определении тождества речь идет в пособиях и учебниках по математике для 7 класса, так как школьная программа для семиклассников предполагает проведение действий исключительно с целыми выражениями (одно- и многочленами). Они имеют смысл при любых значениях переменных, которые входят в их состав.
Программа 8 класса расширяется за счет рассмотрения выражений, которые имеют смысл только для значений переменных из ОДЗ. В связи с этим и определение тождества меняется. Фактически, тождество становится частным случаем равенства, так как не каждое равенство является тождеством.
Знак тождества
Обычно запись тождества ничем не отличается от записи обыкновенного равенства. Знак тождества может быть применен для того, чтобы подчеркнуть, что перед нами не простое равенство, а тождество.
Примеры тождеств
Обратимся к примерам.
Равенства 2 + 3 = 5 и 7 − 1 = 2 · 3 также можно считать тождествами, так как они являются вернными. Здесь также допустима запись 2 + 3 ≡ 5 и 7 − 1 ≡ 2 · 3 .
Тождества могут содержать не только числа, но также и переменные.
Это значит, что приведенные равенства не являются тождествами.
В математике мы постоянно имеем дело с тождествами. Делая записи действий, производимых с числами, мы работаем с тождествами. Тождествами являются записи свойств степеней, свойств корней и прочие.
Тождество. Тождественные преобразования. Примеры.
Тождества в основном применяются для решения линейных уравнений.
Тождеством называется равенство, которое верно при всех значениях переменных.
Или другими словами, тождество — это равенство, которое выполняется на всём множестве значений переменных, входящих в него, например:
В этих выражениях при всех значениях a и b равенство верное.
2 выражения с равными значениями при всех значениях переменных являются тождественно равными.
Равенство x+2=5 может существовать не при всех значениях x, а лишь при x=3. Это равенство не будет тождеством, это будет уравнением. Кроме того, тождеством будет равенство, которое не содержит переменные, например 25 2 =625.
Тождественное равенство обозначают символом «≡» (тройное равенство).
Примеры тождеств.
— Тождество Эйлера (кватернионы);
— Тождество Эйлера (теория чисел);
— Тождество четырёх квадратов;
— Тождество восьми квадратов;
Тождественные преобразования.
Тождественное преобразование выражения (преобразование выражения) – это подмена одних выражений другими, тождественно равными друг другу.
Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.
Выполним тождественные преобразования с такой дробью: 
.
Полученное тождество, при х ≠ 0 и х ≠ 1 (недопустимые значения), т.к. знаменатель левой части не может быть равен нулю.
Доказательство тождеств.
Для того, чтоб доказать тождество нужно сделать тождественные преобразования обеих или одной части равенства, и получить слева и справа одинаковые алгебраические выражения.
Например, доказать тождество:
Вынесем х за скобки:
Это равенство есть тождество, при х≠0 и х≠1.
Чтоб доказать, что равенство не является тождеством, нужно найти 1-но значение переменной (которое допустимо) у которой числовые выражения (которые были получены) станут не равными друг другу.
5−1 ≠ 5+1 — подставим, к примеру, 5.
Это равенство не тождество.
Разница между тождеством и уравнением.
Тождество верно при всех значениях переменных, а уравнение – это равенство, которое верно только при одном либо нескольких значениях переменной.
Это выражение верно лишь при х = 10.
Тождеством будет равенство, которое не содержит переменных.
Лекция №3. Доказательство тождеств
ЛЕКЦИЯ №3 Доказательство тождеств
Цель: 1. Повторить определения тождества и тождественно равных выражений.
2.Ввести понятие тождественного преобразования выражений.
3. Умножение многочлена на многочлен.
4. Разложение многочлена на множители способом группировки.
Пусть каждый день и каждый час
Пусть добрым будет ум у нас,
А сердце умным будет!
В математике существует множество понятий. Одно из них тождество.
Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят. Некоторые тождества мы уже знаем.
Например, все формулы сокращенного умножения являются тождествами.
Формулы сокращенного умножения
4. a3 ± b3 = (a ± b)(a2 
ab + b2).
Доказать тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части.
В алгебре существует несколько различных способов доказательства тождеств.
Способы доказательства тождеств
- Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным. Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным. Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Как видите способов достаточно много. Какой способ выбрать в данном конкретном случае, зависит от тождества, которое вам необходимо доказать. По мере того, как вы будете доказывать различные тождества, придет и опыт в выборе способа доказательства.
Пример 1. Докажите тождество x·(a+b) + a·(b-x) = b·(a+x).
Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.
x·(a+b) + a·(b-x) = x·a +x·b + a·b – a·x.
Приведем подобные слагаемые и вынесем общий множитель за скобку.
x·a + x·b + a·b – a·x = x·b + a·b = b·(a + x).
Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.
В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.
(a+5)·(a+2) = (a²) + 5·a +2·a +10 = a²+7·a + 10.
Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.
« Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения»
Выяснить какое равенство является тождеством:
«Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений»
Умножение многочлена на многочлен
Умножим многочлен a + b на многочлен c + d. Составим произведение этих многочленов:
(a+b)(c+d).
Обозначим двучлен a + b буквой x и преобразуем полученное произведение по правилу умножения одночлена на многочлен:
(a+b)(c+d) = x(c+d) = xc + xd.
В выражение xc + xd. подставим вместо x многочлен a+b и снова воспользуемся правилом умножения одночлена на многочлен:
xc + xd = (a+b)c + (a+b)d = ac + bc + ad + bd.
Итак: (a+b)(c+d) = ac + bc + ad + bd.
Произведение многочленов a + b и c + d мы представили в виде многочлена ac + bc + ad + bd. Этот многочлен является суммой всех одночленов, получающихся при умножении каждого члена многочлена a + b на каждый член многочлена c + d.
Вывод: произведение любых двух многочленов можно представить в виде многочлена.
Правило: чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Заметим, что при умножении многочлена, содержащего m членов на многочлен, содержащий n членов в произведении до приведения подобных членов должно получиться mn членов. Этим можно воспользоваться для контроля.
Разложение многочлена на множители способом группировки:
1. Способы доказательства тождеств.
2. Что называют тождественным преобразованием выражения.
3. Умножение многочлена на многочлен.
4. Разложение многочлена на множители способом группировки
Доказательства тождеств
Доказательство тождеств. В математике существует множество понятий. Одно из них тождество.
Некоторые тождества мы уже знаем. Например, все формулы сокращенного умножения являются тождествами.
Доказать тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части.
В алгебре существует несколько различных способов доказательства тождеств.
Способы доказательства тождеств
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Как видите способов достаточно много. Какой способ выбрать в данном конкретном случае, зависит от тождества, которое вам необходимо доказать. По мере того, как вы будете доказывать различные тождества, придет и опыт в выборе способа доказательства.
Рассмотрим несколько простых примеров
Пример 1.
Докажите тождество x*(a+b) + a*(b-x) = b*(a+x).
Решение.
Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.
Приведем подобные слагаемые и вынесем общий множитель за скобку.
Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.
Пример 2.
Докажите тождество a^2 + 7*a + 10 = (a+5)*(a+2).
Решение.
В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.
Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.